Procesos Estocásticos - Facultad de Ciencias Exactas

Teoría de la Información
Tratamiento probabilístico de la
Información
Fuentes de información
(continuación)
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Cálculo del vector estacionario
V* = M . V*
 (M – I) V* = 0
 Vi * = 1
Sistema de
ecuaciones
Condiciones de existencia de V*:
- conjunto finito de estados
- fuente ergódica (todos los estados del proceso son alcanzables desde
otro estado y no hay estados o clases absorbentes)
ergódico
no ergódicos
estado
absorbente
clase de estados
absorbentes
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
1
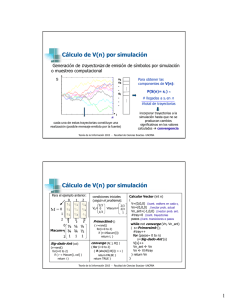
Simulación en estado estacionario
Cuando un proceso se encuentra en estado estacionario es más sencillo
efectuar los cálculos por muestreo computacional, ya que es suficiente
simular una única trayectoria (o realización del proceso)
Ejemplo: Cálculo de V* por muestreo computacional
•
•
•
registrar la cantidad de veces que se emite cada símbolo
dividir por el total de transiciones para obtener las probabilidades de estado
mientras no se produzca la convergencia del vector de estado
 generar nuevos pasos de simulación y recalcular los valores de probab.
X
0
2
1
0
1 1
0
0
2
0
t
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Estado estacionario por muestreo comput.
Para el ejemplo anterior:
0
1
2
condición inicial
(arbitraria)
Por ej:
0
1
V0 =
2
0
1
2
0
½ ¼ ¼
¾ ¾ ½
1 1
2 1
Macum=1
Sig-dado-Ant (Macum, col)
{r=rand()
for(i=0 to 2)
if ( r < Macum[i,col] )
return i; }
2/3
0
1/3
V0acum= 2/3
2/3
1
Primerpaso (V0acum)
{ r=rand()
for(i=0 to 2)
if (r<V0acum[i])
return i; }
Calcular Vector_estac
{ V=V*= (0,0,0) //vector actual
V_ant=(-1,0,0) //vector anterior
pasos= 0
s=Primerpaso (V0acum);
while no converge (V, V_ant)
{ s=Sig-dado-Ant (Macum,s)
pasos++; V[s]++
V_ant  V*
V*  V/#pasos
}  V* //estado estac.
}
converge (A[ ], B[] )
{ for (i=0 to 2)
{ if (abs(A[i]-B[i]) > E )
return FALSE }
return TRUE }
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
2
Transición en n pasos
En una fuente markoviana homogéna
cuál es la probabilidad de que, si la fuente emitió el símbolo i en un
cierto instante, emita el símbolo j luego de n transiciones?
Suponiendo que n=n1+n2 :
p j /i
( n1 n 2 )
  pk / i
( n1)
. pj/k
( n 2)
k
M(n1+n2) = M(n2) . M(n1)
1º ecuación de Chapman-Kolmogorov
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Transición en n pasos
(cont.)
Ejemplo:
n= 2:
Matriz de transición
en 2 pasos
M
M
.
n= 3:
M2
.
Matriz de transición en
3 pasos
M
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
3
Primera transición en n pasos
Cuál es la probabilidad de que se dé la transición de un símbolo i
a un símbolo j, por primera vez, en n pasos?  fj/i(n)
n= 1: pj/i(1) = fj/i(1)
n= 2: pj/i(2) = fj/i(1) . pj/j(1) + fj/i(2)
 fj/i(2) = pj/i(2) - fj/i(1).pj/j(1)
n= 3: pj/i(3) = fj/i(1) . pj/j(2) + fj/i(2) . pj/j(1) + fj/i(3)
 fj/i(3) = pj/i(3) - fj/i(1).pj/j(2) - fj/i(2).pj/j(1)
En general:
f j / i ( n)  p j / i ( n) 
n 1
f
m 1
j/i
(m) . p j / j (n  m)
2º ecuación de Chapman-Kolmogorov
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Transición eventual
Cuál es la probabilidad de que eventualmente se produzca la
transición del símbolo i al símbolo j durante la evolución del
proceso?

f
n 1
j/i
( n)  F j / i
• Si Fj/i = 1  la transición de i a j se produce con seguridad
• Si Fj/i < 1  existe la posibilidad de que no se produzca la transición
de i a j
ejemplo:
F3/1 ?
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
4
Media de primera transición
Si Fj/i = 1, las {fj/i(n)} conforman una distribución de probabilidad
de la variable “número de pasos para ir de si a sj por 1ra. vez”
y se puede calcular su media  “tiempo medio de espera”

 j / i   n . f j / i ( n)
n 1
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Primera recurrencia en n pasos
Si i=j, fi/i(n) = probabilidad de primera recurrencia del símbolo i
f i / i ( n)  p i / i ( n) 
n 1
f
m 1
i/i
(m) . pi / i (n  m)
Si Fi/i =1 (probabilidad de retorno eventual al símbolo i

 i / i   n . f i / i ( n)
Ejemplo:
n 1
Tiempo medio de
primera recurrencia
n= 1: f0/0(1) = p0/0(1) = 1/4
n= 2: f0/0(2) = 3/4 . 1 = 3/4
n= 3: f0/0(3) = 0
μ0/0= 1. ¼+2. ¾
= 7/4 = 1.75
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
5
μi/i por muestreo computacional
Procesar la cadena markoviana generada por muestreo, calculando el
número de pasos entre los retornos al símbolo i :
• sumar la cantidad de pasos entre ocurrencias sucesivas del símbolo i
• dividir por la cantidad de retornos a i para obtener μi/i
• verificar la convergencia de μi/i
Ejemplo:
µ0/0
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Indicadores Estadísticos
• Media:
 S (t )   s   si P(S (t )  si )
i
• Desvío Standard:
 (t ) 
 ( s  s)
i
2
P(S (t )  si )
i
• Autocorrelación:
R(t1, t 2)   S (t1), S (t 2)    si s j P( S (t1 )  si , S (t 2 )  s j )
i
j
• Autocovarianza:
C(t1, t 2)   S (t1), S (t 2)    S (t1)  S (t 2) 
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
6
Indicadores cruzados
• Correlación cruzada:
RXY (t1, t 2)   X (t1), Y (t 2) 
•
X(t)
Y(t)
Covarianza cruzada:
C XY (t1, t 2)   X (t1), Y (t 2)    X (t1)  Y (t 2) 
• si CXY(t1,t2) = 0
 t1  t 2 , se dice que los procesos están decorrelacionados
• si RXY(t1,t2) = 0,
 t1  t 2 , se dice que los procesos son ortogonales
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Correlación cruzada- Aplicaciones
Estos indicadores permiten analizar el grado de relación entre dos fuentes
de información (señales, imágenes, ...)
Valores altos (picos) indican mayor acople
ALGUNAS APLICACIONES:
• Reconocimiento de patrones
• Registración de imágenes (seguimiento satelital o fusión de estudios médicos, etc.)
• Identificación biométrica (por huellas dactilares, por el iris, señal de voz, etc.)
• Análisis de procesos económicos, sociales, ambientales, etc.
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
7
Cálculo analítico (resumen)
En tiempos particulares
En estado estacionario
Probabilidad de estado para t≥test
Probabilidad de estado
P(X(t1)= x1)
P(X(t1)= x2)
P(X(t1)= xi)
P(X(t)= x1)
P(X(t)= x2)
=
…
V(t1)
=
P(X(t)= xi)
V*
…
P(X(t1)= xn)
P(X(t)= xn)
Resolver el sistema de ecuaciones
En 1 paso de t-1 a t
(M – I) V* = 0
 V*[i] = 1
V(t) = M .V(t-1)
En n pasos de t-n a t
n>0
V(t) = Mn .V(t-n)
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
Cálculo analítico (resumen)
pj/i(n) probabilidad
de transición en n pasos
1º ecuación de Chapman-Kolmogorov
p j /i
( nm)
  pk / i
(n)
. pj/k
( m)
M(n+m)= M(m).M(n)
k
fj/i(n) probabilidad de primera
transición en n pasos
fi/i(n) probabilidad de primera
recurrencia en n pasos
j/i
2º ecuación de Chapman-Kolmogorov
n 1
f j / i ( n)  p j / i ( n) 
f
f i / i (n)  pi / i (n) 
f
m 1
(m) . p j / j (n  m)
i/i
(m) . pi / i (n  m)
n 1
m 1

media de primera
transición
 j / i   n . f j / i ( n)
i/i
i / i 
media de primera
recurrencia
j/i
n 1

 n. f
n 1
i/i
( n)
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
8
Muestreo computacional (resumen)
En tiempos particulares
En estado estacionario
Probabilidad de estado en tn
Probabilidad de estado para t≥test
X
X
t
Varias trayectorias
V(t1)=
una trayectoria
tn
t
P(S(t 1 )  s1 )  # llegadas en t1 a s1 # trayectori as
P(S(t)  s1 )  # veces que pasó por s1 # pasos
P(S(t 1 )  s 2 )  # llegadas en t1 a s2 # trayectori as
P(S(t)  s 2 )  # veces que pasó por s2 # pasos
…
P(S(t 1 )  s n )  # llegadas en t1 a sn # trayectori as
Se agregan trayectorias hasta convergencia del vector
V*=
…
P(S(t)  s n )  # veces que pasó por sn # pasos
Se agregan más pasos hasta convergencia del
vector
Teoría de la Información 2014 - Facultad de Ciencias Exactas- UNCPBA
9