Desarrollo Formal de Programas Desarrollar software: estrategias

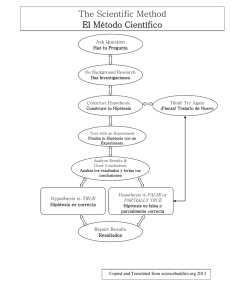
Working Hypothesis
Desarrollo Formal de Programas
Desarrollar software: estrategias
Camilo Rueda 1
1 Universidad
Javeriana-Cali
PUJ 2010
Working Hypothesis
Sistemas de software: especificación
Contexto
Propiedades de los datos
del programa
Variables
Guardan los resultados
del programa
Invariante
Especifica solamente los tipos
de las variables
Working Hypothesis
Especificación: los eventos
Inicialización
Valores iniciales de
variables de salida
Eventos finales
Especifican la poscondición
del programa
Working Hypothesis
Refinamiento
Imaginar un proceso
Imaginar que se detiene ese proceso en un punto
Definir variables para especificar el punto de detención
Establecer lo que se cumple del programa en el punto de
detención (invariante)
inicializar variables de modo que cumplan el invariante
Deducir del invariante las condiciones de terminacin
escribir los eventos
Working Hypothesis
Estrategias de prueba
Probadores de Rodin son muy poderosos
Ensayar siempre primero algunos de ellos, en el orden:
P0, M0 ,Npp/R, Npp/R with Lasso, P1
Si lo anterior no funciona,
Asegurarse primero de que el objetivo
se puede probar
Working Hypothesis
Estrategias de prueba (2)
Hay estrategias que funcionan muchas veces:
ah
dc
instanciar
particularizar
agregar hipótesis
prueba por casos
objetivo es un existencial
hipótesis es un cuantificador universal
Working Hypothesis
Estrategias de prueba: ejemplo
Objetivo: maxsuma ≥ fsuma(j)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
sumactual + s(i + 1) ≤ maxsuma
Hipótesis:
i 6= n
j ∈ 1 .. i + 1
Note que si se supiera que
j ∈ 1 .. i
entonces estarı́a ya probado!
Working Hypothesis
Estrategias de prueba: ejemplo
Objetivo: maxsuma ≥ fsuma(j)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
sumactual + s(i + 1) ≤ maxsuma
Hipótesis:
i 6= n
j ∈ 1 .. i + 1
Note que si se supiera que
j ∈ 1 .. i
entonces estarı́a ya probado!
Casos:
i ∈ 1 .. i
→ a)
b)
i∈
6 1 .. i
Working Hypothesis
Estrategias de prueba: ejemplo, cont.
Objetivo: maxsuma ≥ fsuma(j)
Casos:
a)
i ∈ 1 .. i
b)
i∈
6 1 .. i
Escribir en Rodin j ∈ 1 .. i, y oprimir el botón dc.
Prueba del caso a):
particularizar con j la hipótesis
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
q.e.d
Working Hypothesis
Estrategias de prueba: ejemplo, cont.
Objetivo: maxsuma ≥ fsuma(j)
Prueba del caso b):
Casos:
a)
i ∈ 1 .. i
b)
i∈
6 1 .. i
agregar la hipótesis j = i + 1
probarla con P0
Rodin reescribe el objetivo:
maxsuma ≥ fsuma(i + 1)
Working Hypothesis
Estrategias de prueba: ejemplo, cont.
Objetivo: maxsuma ≥ fsuma(i + 1)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
Hipótesis: sumactual + s(i + 1) ≤ maxsuma
i 6= n
Se puede probar?
Working Hypothesis
Estrategias de prueba: ejemplo, cont.
Objetivo: maxsuma ≥ fsuma(i + 1)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
Hipótesis: sumactual + s(i + 1) ≤ maxsuma
i 6= n
Se puede probar?
No, porque no hay hipótesis que definan fsuma(i + 1)
Hay que agregarlas (con el lazo)
Working Hypothesis
Ejemplo, prueba del caso b)
Objetivo: maxsuma ≥ fsuma(i + 1)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
Hipótesis: sumactual + s(i + 1) ≤ maxsuma
i 6= n
Nuevas Hipótesis:
∀k . k ∈ 1 .. (n − 1) ⇒ fsuma(k + 1) = fsuma(k ) + s(k + 1)
fsuma(i) + s(i + 1) ≤ maxsuma
Se puede probar?
Working Hypothesis
Ejemplo, prueba del caso b)
Objetivo: maxsuma ≥ fsuma(i + 1)
∀j. j ∈ 1 .. i ⇒ maxsuma ≥ fsuma(j)
Hipótesis: sumactual + s(i + 1) ≤ maxsuma
i 6= n
Nuevas Hipótesis:
∀k . k ∈ 1 .. (n − 1) ⇒ fsuma(k + 1) = fsuma(k ) + s(k + 1)
fsuma(i) + s(i + 1) ≤ maxsuma
Se puede probar? Si, siempre y cuando i ∈ 1 .. (n − 1)
y esto es cierto!