1 tema 6: reactores multifasicos gas-liquido

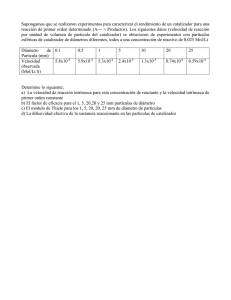
TEMA 6: REACTORES MULTIFASICOS GAS-LIQUIDO-SOLIDO CATALITICO
1
2
6.1 Diseño de reactores con el sólido en suspensión (slurry).
6.1.1 Columnas de borboteo slurry:
• La velocidad superficial del gas mínima para asegurar la suspensión se
calcula mediante la expresión de Narayan et al.(1969)
n
⎛D⎞
v SGm = α ⎜ ⎟ u f exp(- β ε p ) (CGS units)
⎝2⎠
D = di metro de la columna
γ
0.5
u f + 3.687 H S ( u f ) = φ
H S (cm) = altura del s lido en suspensi n
⎛
⎡2d
ε pHS ⎤
φ = ⎜ 2g( ρ p - ρ L )⎢ p +
⎥
⎜
3 ρ L ρ p + ε p ρ L ⎦⎥
⎢
⎣
⎝
0.5
⎞
⎟
⎟
⎠
γ = 0.5 para u f < 6.7 cm s-1
γ = 0.19 para 6.7 < u f < 21.3 cm s-1
ε p = fracci n de reactor ocupada por las partÍculas
n = 0.2 para d p ≤ 100 μm
n = 0.5 para d p > 200 μm
εp < 0.1
εp > 0.1
α
β
4.3
1.25
10
3
3
• Holdup de gas
⎡
⎤
⎥
1/4 ⎢
⎛ μ L u GS ⎞ ⎢ u GS ⎥
ε = 1.23 ⎜
⎟ ⎢
1/4 ⎥
⎝ σL ⎠ ⎢ ⎛ σL g ⎞ ⎥
⎢⎣ ⎜⎝ ρL ⎟⎠ ⎥⎦
1/2
• Transferencia de materia gas-líquido
db < 2,5 mm, tamaño usual en este tipo de reactores.
⎛ μL ⎞
k L(cm / s) ⎜
⎟
⎝ ρ L DL ⎠
2/3
⎛ Δρ μ g ⎞
= 0.31⎜ LG2 L ⎟
ρL
⎝
⎠
1/3
⎛ Δρ μ g ⎞
= 0.41⎜ LG2 L ⎟
ρL
⎝
⎠
1/3
C.G.S
db > 2,5 mm
⎛ μL ⎞
k L(cm / s) ⎜
⎟
⎝ ρ L DL ⎠
•
1/2
C.G.S
Transferencia de materia líquido-sólido Sano et al. (1974)
(ver en tanque agitado)
• Modelización: Gas FP, Líquido y cata MP
1. Líquido inerte. Para el gas
G
- d w AG - ( N Aa)GL dV = 0
( N Aa)GL = ( N Aa)LS = − r A
V
=
w Ao
X As
∫
X Ae
dX A
( −r A )
4
L
S
− r A = k o a S cG
⎛ 1
a 1
a H
1
1 ⎞
= s
+ s A + HA ⎜ +
⎟
k o aG k G aG k L
⎝ ks η k ⎠
a j , definidas por unidad de volumen de líquido
π db2
6 VB
aG =
VB =
3
dB
π db / 6
aS =
π dp2
1
6 mS
mS =
π d / 6 ρp
d p ρp
3
p
VB , volumen burbuja por unidad volumen líquido
m S , carga catalizador (kg cata / m 3 líquido)
En general, la carga de catalizador suele estar en el rango 1 al 5% en peso.
2. Líquido reactante flujo en MP
L
G
S
A
B
A
5
6.1.2 Reactores tanque agitado:
• Transferencia líquido-sólido se puede utilizar la expresión de Sano et
al.
1/4
(Sh )S = [2 + 0.4(Re) (Sc)1/3
L ] φC
φ C(factor superficial Carman) =
(Sh )S =
(Sc)L =
k ASd p
D AL
μL
ρ L D AL
4
Re =
6ε p
a Sd p
3
∑ Ld p ρ L
3
μL
ΣL la potencia disipada por el agitador, P (W/kg), la cual se calcula de la
siguiente manera. (Columna burbujeo ΣL = uSG g)
ρN R D2A
′
Re=
μ
2
N D
Fr = R A
g
N R = velocidad de rotación del agitador
DA = diámetro característico del agitador
P
Ne =
= Número de potencia de Newton
3
5
ρ N R DA
Ne = C(R′e) Fr b
a
Φ=
Ne
Fr
b
= C (R′e) = factor de potencia
a
ρ = ρp εs + ρL εL
μ=
μL
⎛ 1 - εS ⎞
⎜
⎟
⎝ ε S′ ⎠
1'8
a y b tipo agitador
Φ es una función en la bibliografía para cada tipo de agitador.
ε S′ = fracción volumétrica de só lido en lecho fijo, despues sedimentación
6
•
Velocidad agitación mínima para mantener sólido en suspensión
α
N'R(congas)- NR >200
0.45
0.45
0.1
0.2
⎛ DR ⎞ g (ρp - ρL ) μ L dp w s0.13
N Rm(sin gas) = ψ⎜
⎟
0.85 0.55
DA ρL
⎝ DA ⎠
w S = % en peso de sólido en el líquido
qG
3
DA
ψ y α dependen de las características del agitador
ψ = 1.5 α = 1.4 para turbinas y impulsores con paletas rectas
• transferencia gas-líquido
⎛ PW ⎞
k L(cm / s) = 0.592 D ⎜
⎟
⎝ ν ⎠
1/4
1/2
A
P W (erg / s) = Ne ρL N 3R D5A
ϕ
WL
μ cm 2
=
s
ρ
WL = masa de líquido en el slurry
ν = viscosidad cinemática =
ϕ = 1 - 12.6
qG
C.G.S
Modelización: MP para gas, líquido y sólido
7
si
qG
< 0.035
3
NRD
NRDA
ϕ, factor correcciónpresenciaburbujas
3
A
6.2 Diseño de reactores G-L-S de lecho fijo.
6.2.1 Reactor G-L-S de lecho fijo y flujo en cocorriente
8
9
10
11
6.2.1.1. Hidrodinámica reactor de lecho fijo y flujo en cocorriente
descendente
12
13
Perdida de presión y holdup:
14
⎛ ΔP ⎞
se estiman por la ecuación de ergun como si circulan
⎜
⎟
⎝ H ⎠ L,G
independientemente cada una de las fases.
χ parámetro deLock-hart-Martinelli
Un esquema de cálculo para una interacción ligera gas-líquido (no espumante
podría ser
⎛ ΔP ⎞
'
⎜
⎟ → χ → Φ L → δ LG
⎝ H ⎠ L,G
⎛ ΔP ⎞
↓→ ε L →↓→ ⎜
⎟
⎝ H ⎠ LG
con ε G = 1 − ε P − ε L
↑ εP
↑ εG
Transferencia de materia película gaseosa
Para calcular kG Reiss propone en condiciones de fuerte interacción
(pulsos y en spray) las siguientes expresiones
⎛ ΔP ⎞
0.66
k G aG = 2 + 0.1 EG (SI)
EG = ⎜
⎟ u SG
⎝ H ⎠ LG
Suele ser despreciable para los trickle beds, ya que normalmente trabajan
con componente puro o ligeramente soluble.
Transferencia de materia película líquida
Reiss (1967) basada en la energía disipada en el flujo a través del lecho
catalítico. Esta energía calculada a partir de la caída de presión y el caudal
másico por unidad de área (L en kg/(m2⋅s)) es
⎛ W ⎞ ⎛ ΔP ⎞
⎛ ΔP ⎞ L
EL ⎜ 3 ⎟ = ⎜
⎟ u SL = ⎜
⎟
⎝ H ⎠ LG ρ L
⎝ m R ⎠ ⎝ H ⎠ LG
15
1) Baja interacción: trickle bed flow, Morsi (1982) para fases acuosas o
orgánicas
⎛ (1 - ε p ) '
k L aL
1/2
Sc
=
1.30
δ LG
⎜⎜
(
)
L
1/3
a
ε
( μL)
S
p
⎝
⎞
⎟⎟
⎠
1.75
(SI)
2) Alta interacción (flujo pulsado) (EL > 60 W/m3), Satterfield (1975)
k La L = 353 ( EL DAL )
0.5
(SI)
Valores típicos:
•
flujo percolación entre 0’01-0’3 s-1
•
régimen pulsos ≥ 1 s-1 , menor resistencia
Para el cálculo del área interfacial
1) Trickle bed, Charpentier (1976)
⎡⎛ ΔP ⎞ (1 - ε p ) ⎤
aL
= 0.05 ⎢⎜
⎥
⎟
ε p aS
⎣⎢⎝ H ⎠ GL ε p aS ⎦⎥
1.2
(SI)
a L ≈ ( 0.2 − 0.8 ) aS
a L , aumenta con espumación
2) Flujo pulsante, Gianetto (1973)
⎡⎛ ΔP ⎞ (1 - ε p ) ⎤
aL
= 0.27 ⎢⎜
⎥
⎟
H
ε p aS
ε
a
⎝
⎠
⎥
GL
p S ⎦
⎣⎢
16
0.48
(SI)
Transferencia de materia Líquido-Sólido
kS, depende caudal de líquido, poca influencia caudal gas.
Dharwadkar y Sylvester (1977) régimen trickle y dP < 3mm
kS
2/3
-0.331
(Sc)L = 1.637 (Re)L
u SL
0.2 < (Re)L =
dp uSLρL
μL
< 2400
(Sc)L =
para dP > 3mm, se utiliza la correlación de Lemay y cols.
k S ( Sc )
2/3
= 0.17
ELμ L
ρL2 ε L
Eficacia de mojado
La eficacia de mojado se estima por la expresión de Mills y Dudukovic (1981),
fe =
área catalizador mojada
=
área total catalizador
2
⎡
⎤
−0.171 ⎛ a S d P ⎞
0.333
0.195
= tanh ⎢ 0.664 ReL FrL WeL ⎜ 2 ⎟ ⎥
⎝ ε L+G ⎠ ⎦
⎣
u L dp ρL
aS L2m
L2m
ReL =
; FrL (Froude) = 2 ; WeL (Weber) =
μL
ρL g
σ L ρL aS
ε B = porosidad lecho (líquido + gas) = ε L+ G
Modelización
17
μL
ρL D AL
Reacción catalizada
A(g) + B(l) → R(g,l,s)
Hipótesis:
• Flujo en pistón para ambas fases
• Factor de mojado 1
• Condiciones isotermas
• Buena distribución líquido y sólido con, D/dP ≥ 20.
• Cinética primer orden para A y B
r = -rA = -rB = k cAS cBS
Ecuación general velocidad para A, incluye: 1. transporte película gaseosa; 2.
equilibrio interfase; 3. transporte película líquida; 4. transporte película
liquido- sólido; 5. difusión y reacción en el catalizador,
−rA =
1 / HA
c
( 1 − ε B ) ρP + ( 1 − εB ) ρP + 1 + 1 Ag
H A k AG aG
k AL aL
k AS aS η k cBS
− rA = k OAc Ag
( mol / gcata s )
18
(mol / g cata s)
La conductancia global, kOA (m3 gas/gcat s), depende también de cBS.
Ecuación general para el reactante B, incluye: 4. transporte película líquida
superficie externa catalizador; y 5. difusión y reacción en el catalizador
−rB =
1
1
1
+
k BS aS η k c AS
− rB = k OB cBL
cBL
(mol / g cat s)
(mol / g cat s)
La conductancia global, kOB (m3 gas/gcat s), depende también de cAS.
Solución simultánea de los balances molares de A y B con sus respectivas
ecuaciones globales cinéticas
Balance molar de A (flujo en pistón)
d wA
= rA = − k OA c AG
dW
Balance molar de B (flujo en pistón)
d wB
dc
= q L BL = rB = −k OB cBL
dW
dW
En algunos casos hay solución analítica, sino hay que recurrir a la numérica.
Casos límite:
1.
Baja solubilidad de A (HA, alto), controla el transporte de A y/o el
líquido con elevada concentración de B, como suele suceder en una
oxidación catalítica de un hidrocarburo. Entonces kOA es constante y se
puede integrar los balances molares. Por ejemplo, si además εA = 0 , la
cantidad necesaria de catalizador dada una conversión de gas A viene
dada por
W=
c
qG
q
1
ln A,ent = G ln
k OA c A,sal k OA 1 − X A
19
2. Elevada solubilidad del gas A (HA bajo), líquido saturado de A,
controla
el
transporte
de
B.
Situación
común
en
hidrogenaciones de hidrocarburos. Entonces cAS es constante, y, por
tanto, también lo es kOB. Ahora la cantidad de catalizador necesario se
calcula por
W=
c
qL
q
1
ln B,ent = L ln
k OB cB,sal k OB 1 − XB
En la mayoría de los reactores de goteo comerciales el gas y líquido se mueven
prácticamente en flujo en pistón (dispersión axial despreciable, sobre todo en
la fase gas). Sin embargo, en reactores a menor escala la fase líquida puede
presentar macromezcla (dispersión axial significativa) y en menor proporción
también la fase gaseosa. Para el cálculo de las dispersiones axiales se
recomiendan las relaciones
Hochman and Effron (1969) establecen para flujo trickle:
(Pe)G =
uSG d p
DAG
(Pe)L =
-0.7
⎡ (Re)G ⎤
-0.005(Re)L
= 1.8 ⎢
⎥ 10 εp
⎣⎢ ε p ⎦⎥
uSLd p
D AL
⎡ (Re)L ⎤
= 0.042 ⎢
⎥
⎣ εp ⎦
0.5
La hipótesis de flujo en pistón se pude aplicar siempre que se cumpla el
criterio de Mears (1971)
H
dp
>
20
c (0)
ln BL
(Pe)L cBL(H)
Para conversiones del 90% y partículas entre 1 y 5 mm fácilmente se satisface
esta condición con lo cual se puede considerar flujo en pistón para ambas
fases. La mezcla longitudinal se ha encontrado despreciable para regímenes
de fuerte interacción.
20