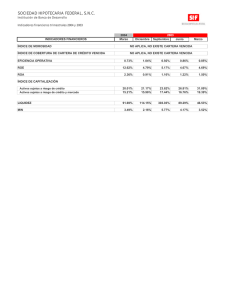
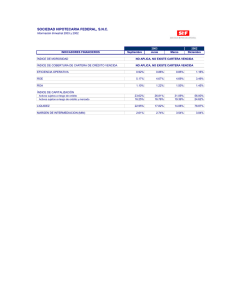
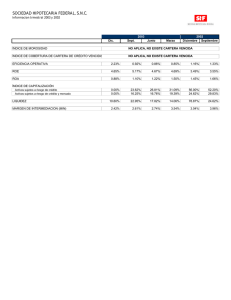
1.2 Comparación de capitales financieros

MÓDULO 1:
FUNDAMENTOS DE LA INVERSIÓN
Índice
Conceptos básicos de la
inversión
2
Concepto de Capital Financiero
3
Comparación de capitales financieros
3
Ley financiera
8
Capitalización simple
14
Capitalización compuesta
22
Introducción
23
Descuento comercial simple
24
Descuento racional simple
26
Descuento racional compuesto
Tipos de interés y
rentabilidad
32
Tipos de interés
34
Rentabilidad
Conceptos estadísticos
44
Media y esperanza
46
Varianza y desviación típica
48
Covarianza y correlación
51
Regresión lineal mínimo cuadrática
62
Rentabilidad
66
Riesgo
69
Supuestos de la hipótesis de normalidad
Capitalización
Descuento
Rentabilidad y riesgo
fikai AULA FINANCIERA
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 1. Conceptos básicos de la inversión
1.1 Fenómeno financiero. Concepto de Capital Financiero
1.2 Comparación de capitales financieros
1.3 Ley financiera
1.3.1 Operación financiera
fikai AULA FINANCIERA
1
1.1 Fenómeno financiero.
Concepto de Capital Financiero
Capítulo 1: Conceptos básicos de la inversión
Cuando se dispone de una cantidad de dinero (capital) se puede destinar, o bien a
gastarlo (satisfaciendo alguna necesidad), o bien a invertirlo para recuperarlo en un
futuro más o menos próximo, según se acuerde.
De la misma manera que estamos dispuestos a gastarlo para satisfacer una
necesidad, estaremos dispuestos a invertir siempre y cuando la compensación
económica nos resulte suficiente. En este sentido el principio básico de la
preferencia de liquidez establece que a igualdad de cantidad los bienes más
cercanos en el tiempo son preferidos a los disponibles en momentos más lejanos. La
razón es el sacrificio del consumo.
Este aprecio de la liquidez es subjetivo pero el mercado de dinero le asigna un valor
objetivo fijando un precio por la financiación que se llama interés. El interés se puede
definir como la compensación por la renuncia temporal del dinero o coste de
oportunidad de no disponer del dinero durante un tiempo.
Esta compensación económica se exige, entre otras, por tres razones básicas:
• Por el riesgo que se asume.
• Por la falta de disponibilidad que supone desprenderse del capital durante un tiempo.
• Por la depreciación del valor del dinero en el tiempo.
La cuantificación de esa compensación económica, de los intereses, depende de tres
variables, a saber:
• La cuantía del capital invertido.
• El tiempo que dura la operación.
• El tanto de interés al que se acuerda la operación.
Cuando se habla de capital financiero (C; t) nos referimos a una cuantía (C) de
unidades monetarias asociada a un momento determinado de tiempo (t).
2
fikai AULA FINANCIERA
1.2 Comparación de capitales financieros
Capítulo 1: Conceptos básicos de la inversión
En una operación financiera no tiene sentido hablar de capitales iguales (aquellos en
los que coinciden cuantías y vencimientos), sino que siempre estaremos refiriéndonos
a capitales equivalentes. Hay equivalencia entre dos capitales cuando a su
propietario le resulta indiferente una situación u otra. Es decir, si resulta indiferente
cobrar hoy 1.000 euros a cobrar 1.050 euros dentro de un año, entonces diremos que
ambos capitales (1.000; 0) y (1.050; 1) son equivalentes.
De una manera más general, dos capitales cualesquiera, C1 con vencimiento en t1 y C2
con vencimiento en t2, son equivalentes cuando se está de acuerdo en intercambiar
uno por otro.
El concepto de equivalencia no significa que no haya ganancia o coste en la
operación. Todo lo contrario, la equivalencia permite cuantificar ese beneficio o
pérdida que estamos dispuestos a asumir en una operación concreta.
1.3 Ley financiera
Capítulo 1: Conceptos básicos de la inversión
Para que una operación financiera se realice es necesario que a los intervinientes las
cuantías que dan y reciben les resulten equivalentes. Es necesario que deudor y
acreedor se pongan de acuerdo en cuantificar los capitales de los que se parte y a los
que finalmente se llega. Esto implica elegir un método matemático que permita dicha
sustitución: una ley financiera. La ley financiera se define como un modelo
matemático (una fórmula) para cuantificar los intereses por el aplazamiento y/o
anticipación de un capital en el tiempo.
Conociendo las diferentes leyes financieras que existen y cómo funcionan se podrán
sustituir unos capitales por otros, pudiéndose formalizar las diferentes operaciones
financieras.
1.3.1 OPERACIÓN FINANCIERA
ƒ CONCEPTO:
Se entiende por operación financiera la sustitución de uno o más capitales por
otro u otros equivalentes en distintos momentos de tiempo, mediante la
aplicación de una ley financiera.
En definitiva, cualquier operación financiera se reduce a un conjunto de flujos de caja
(cobros y pagos) de signo opuesto y distintas cuantías que se suceden en el tiempo.
Así, por ejemplo, la concesión de un préstamo por parte de una entidad bancaria a un
cliente supone para este último un cobro inicial (el importe del préstamo) y unos pagos
periódicos (las cuotas) durante el tiempo que dure la operación. Por parte del banco, la
operación implica un pago inicial único y unos cobros periódicos.
fikai AULA FINANCIERA
3
La realización de una operación financiera implica, por tanto, que se cumplan tres
puntos:
1. Sustitución de capitales. Ha de existir un intercambio de un(os) capital(es)
por otro(s).
2. Equivalencia. Los capitales han de ser equivalentes, es decir, debe resultar de
la aplicación de una ley financiera.
3. Aplicación de una ley financiera. Debe existir acuerdo sobre la forma de
determinar el importe de todos y cada uno de los capitales que compongan la
operación, resultado de la consideración de los intereses generados.
ƒ ELEMENTOS
- Personales
En una operación financiera básica interviene un sujeto (acreedor) que pone a
disposición de otra (deudor) uno o más capitales y que posteriormente recuperará,
incrementados en el importe de los intereses.
La acción de entregar por parte del acreedor y de recibir por parte del deudor se
considerará la prestación de la operación financiera. La operación concluirá cuando
el deudor termine de entregar al acreedor el capital (más los intereses); a esta
actuación por ambas partes se le denomina la contraprestación de la operación
financiera.
En toda operación financiera las cantidades entregadas y recibidas por cada una de
las partes no coinciden. El aplazamiento (o adelantamiento) de un capital en el tiempo
supone la producción de intereses que formarán parte de la operación y que habrá que
considerar y cuantificar. Por tanto, prestación y contraprestación nunca son
aritméticamente iguales. No obstante, habrá una ley financiera que haga que resulten
financieramente equivalentes, es decir, que si valorásemos prestación y
contraprestación en el mismo momento, con la misma ley y con el mismo tanto,
entonces sí se produciría la igualdad numérica entre ambas.
Tanto la prestación como la contraprestación pueden estar formadas por más de un
capital que incluso se pueden solapar en el tiempo.
- Temporales
Al momento de tiempo donde comienza la prestación de la operación financiera se le
denomina origen de la operación financiera. Donde concluye la contraprestación de la
operación financiera se le llama final de la operación financiera. Al intervalo de tiempo
que transcurre entre ambas fechas se le denomina duración de la operación
financiera, durante el cual se generan los intereses.
- Objetivos
La realización de la operación financiera exige un acuerdo sobre aspectos tales como:
la cuantía del capital de partida, la ley financiera que se va a emplear y, finalmente, el
tanto de interés (coste/ganancia) unitario acordado.
4
fikai AULA FINANCIERA
ƒ CLASIFICACIÓN
Según la duración:
• A corto plazo: la duración de la operación no supera el año.
• A largo plazo: aquéllas con una duración superior al año.
Según la ley financiera que opera:
• Según la generación de intereses:
1) En régimen de simple: los intereses generados en el pasado no se acumulan y,
por tanto, no generan, a su vez, intereses en el futuro.
2) En régimen de compuesta: los intereses generados en el pasado sí se
acumulan al capital de partida y generan, a su vez, intereses en el futuro.
• Según el sentido en el que se aplica la ley financiera:
1) De capitalización: sustituye un capital presente por otro capital futuro.
2) De actualización o descuento: sustituye un capital futuro por otro capital
presente.
Según el número de capitales de que consta:
• Simples: constan de un solo capital en la prestación y en la contraprestación.
• Complejas (o compuestas): cuando constan de más de un capital en la prestación
y/o en la contraprestación.
Según el interés:
• A interés explícito: cuando en la operación financiera se producen los intereses al
aplicar el tipo de interés. Por ejemplo, un bono a 5 años con pago anual de intereses.
• A interés implícito: cuando los rendimientos se calculan sobre el valor nominal y se
descuentan de dicho valor nominal. Por ejemplo, una Letra del Tesoro a 12 meses.
fikai AULA FINANCIERA
5
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 2. Capitalización
2.1 Capitalización simple
2.1.1
2.1.2
2.1.3
2.1.4
2.1.5
Definición y fórmula general
Magnitudes derivadas
Tantos equivalentes en capitalización simple
Números comerciales: concepto y cálculo
Interés simple anticipado
2.2 Capitalización compuesta
2.2.1 Definición y fórmula general
2.2.2 Magnitudes derivadas
2.2.3 Tantos equivalentes en capitalización compuesta
fikai AULA FINANCIERA
7
2.1 Capitalización simple
Capítulo 2: Capitalización
2.1.1 DEFINICIÓN Y FÓRMULA GENERAL
Las operaciones en régimen de capitalización simple se caracterizan porque los
intereses, a medida que se van generando, no se acumulan y no generan
intereses en períodos siguientes (no son productivos). De esta forma los intereses
que se producen en cada período se calculan siempre sobre el mismo capital – el
inicial –, al tipo de interés vigente en cada período.
Este régimen financiero es propio de operaciones a corto plazo (menos de un año),
salvo que las condiciones de la operación indiquen lo contrario.
ƒ CONCEPTO:
Operación financiera cuyo objeto es la sustitución de un capital presente por otro
equivalente con vencimiento posterior, mediante la aplicación de la ley financiera en
régimen de simple.
ƒ DESCRIPCIÓN DE LA OPERACIÓN:
Partiendo de un capital (C0) del que se dispone inicialmente – capital inicial –, se trata
de determinar la cuantía final (Cn) que se recuperará en el futuro sabiendo las
condiciones en las que la operación se contrata (tiempo “n” y tipo de interés “i”).
ƒ CARACTERÍSTICAS DE LA OPERACIÓN:
Los intereses no son productivos, lo que significa que:
• A medida que se generan no se acumulan al capital inicial para producir
nuevos intereses en el futuro y, por tanto
• Los intereses de cualquier período siempre los genera el capital inicial (C0),
al tanto de interés vigente en dicho período.
Así pues, la fórmula general del valor de los intereses en capitalización simple, en el
caso de que el tipo de interés sea constante, es:
I = C0 · i · n
donde: i = Tipo de interés nominal expresado en tanto por uno y referido a un año.
n = Duración de la operación, expresada en años.
8
fikai AULA FINANCIERA
ƒ DESARROLLO DE LA OPERACIÓN:
El capital al final de cada período es el resultado de añadir al capital existente al inicio
del mismo los intereses generados durante dicho período. De esta forma, la evolución
del montante conseguido es el siguiente:
Cn = Co + I
sustituyendo los intereses por la expresión I = C 0 · i · n
Cn = Co + (Co · i · n)
Cn = C 0 · ( 1 + i · n )
Por tanto:
Siendo el factor de capitalización = (1 + i · n)
Expresión aplicable cuando el tipo de interés de la operación se mantiene constante
todos los períodos.
A partir de la expresión anterior (denominada fórmula fundamental de la capitalización
simple) no solamente se pueden calcular montantes sino que, conocidos tres datos
cualesquiera, se podría despejar el cuarto restante.
Finalmente, hay que tener en cuenta que «n» lo que indica es el número de veces
que se han generado (y acumulado) intereses al capital inicial, por tanto, esa
variable siempre ha de estar en la misma unidad de tiempo que el tipo de interés
(no importando cuál sea).
ƒ CASO TIPO DE INTERÉS VARIABLE:
Si el tipo de interés es variable la expresión para obtener el capital final o montante
sería:
n
C n = C 0 · ( 1 + i1 + i2 + i3 + ... + in ) = C 0 ·( 1 +
∑i )
j
j =1
fikai AULA FINANCIERA
9
►EJEMPLO RESUELTO
Cálculo del montante en C.S. i = cte
Calcular el montante obtenido al invertir 2.000 euros al 8% anual durante 4 años en
régimen de capitalización simple.
Co = 2.000 €
C4= ?
i = 8% = 0,08
0
4 años
Para calcular el montante utilizamos la expresión:
Cn = C0 · ( 1 + i · n )
C4= 2.000 · (1 + 0,08 x 4 ) = 2.640 €
►EJEMPLO RESUELTO
Cálculo del montante en C.S. i = vble
Se quiere conocer qué capital podremos retirar dentro de 3 años si hoy colocamos
1.000 euros al 5% de interés anual simple para el primer año y cada año nos suben el
tipo de interés simple un punto porcentual.
En este caso al ser el tipo de interés variable, para calcular el capital final, aplicaremos
la expresión:
n
Cn = C 0 · ( 1 + i1 + i2 + i3 + ... + in ) = C 0 ·( 1 +
∑i )
j
j =1
C3 = C0 · ( 1+ i1 + i2 + i3 ) = 1000 · ( 1+ 0,05 + 0,06 + 0,07 ) = 1180 €
10
fikai AULA FINANCIERA
2.1.2 MAGNITUDES DERIVADAS
ƒ CÁLCULO DEL CAPITAL INICIAL:
Partiendo de la fórmula del capital final o montante y conocidos éste, la duración de la
operación y el tanto de interés (cte), bastará con despejar de la misma:
Cn = Co · ( 1 + n · i )
despejando C0 resulta:
C0 =
Cn
1+ n · i
►EJEMPLO RESUELTO
Cálculo del capital inicial en C.S. i = cte
¿Cuánto deberé invertir hoy si quiero disponer dentro de 2 años de 1.500 euros para
comprarme un coche, si me aseguran un 6% de interés anual simple para ese plazo?
Co = ?
Cn= 1500 €
i = 6% = 0,06
0
C0 =
2 años
Cn
1500
=
= 1339,29 €
1 + n · i 1 + 2 · 0,06
ƒ CÁLCULO DE LOS INTERESES TOTALES:
Bastará con calcular los intereses de cada período, que siempre los genera el capital
inicial y sumarlos.
Intereses totales = I1 + I2 + … + In = C0 i1 + C0 i2 + … + C0 in
Luego:
n
Intereses totales = C 0 · ( i1 + i 2 + ... + in ) = C 0 ·
∑i
j
j=1
Si i1 = i2 = … = in = i = cte
Intereses totales = I1 + I2 + … + In = C 0 i + C 0 i + … + C 0 i = C 0 ·n·i
Por último, si conocemos los capitales inicial y final: I = Cn - C 0
fikai AULA FINANCIERA
11
►EJEMPLO RESUELTO
Cálculo de los intereses en C.S. i = cte
¿Qué intereses producirán 300 euros invertidos 4 años al 7% simple anual?
Por suma de los intereses de cada período:
Intereses totales = I1 + I2 + I3 + I4 = C0 i + C0 i + C0 i + C0 i = = C0 x i x 4 =
= 300 x 0,07 x 4 = 84 €
También se puede obtener por diferencias entre el capital final y el inicial:
In = 384 – 300 = 84 €
C4 = 300 x (1 + 0,07 x 4) = 384
►EJEMPLO RESUELTO
Cálculo de los intereses en C.S. i = cte
¿Qué interés producirán 6.000 euros invertidos 8 meses al 1% simple mensual?
In = C0 · i · n = 6.000 x 0,01 x 8 = 480 €
ƒ CÁLCULO DEL TIPO DE INTERÉS:
Si se conocen el resto de elementos de la operación: capital inicial, capital final y
duración, basta con tener en cuenta la fórmula general de la capitalización simple y
despejar la variable desconocida.
Cn
= 1+ n · i
C0
Cn = C0 · (1 + n · i)
►EJEMPLO RESUELTO
Cn
-1= n·i
C0
Cn
-1
C0
i=
n
Cálculo del tipo de interés en C.S. i = cte
Determinar el tanto de interés anual a que deben invertirse 1.000 euros para que en 5
años se obtenga un montante de 1.500 euros.
DATOS: Co = 1000 €
Calculamos i :
Cn = 1500 €
Cn
-1
C0
=
i=
n
n = 5 años
1500
-1
1000
= 0,10 = 10%
5
ƒ CÁLCULO DE LA DURACIÓN:
Por último, conociendo C0, Cn y el tipo de interés i, podemos calcular la duración
mediante la expresión:
Cn
-1
C0
Cn - C 0
I
=
=
n=
i
C0 · i
C0 · i
12
fikai AULA FINANCIERA
2.1.3 TANTOS EQUIVALENTES EN CAPITALIZACIÓN SIMPLE
Dos tantos cualesquiera, expresados en distintas unidades de tiempo, son tantos
equivalentes cuando aplicados a un mismo capital inicial y durante un mismo
período de tiempo producen el mismo interés o generan el mismo capital final o
montante.
RELACIÓN DE EQUIVALENCIA entre el tipo de interés anual ( i ) y el tipo de interés
efectivo fraccionado ( ik ):
El montante obtenido utilizando i :
y utilizando ik :
Cn = C0 · (1 + n · i)
Cn = C0 · (1 + n·k · ik)
donde k es la frecuencia de capitalización, que indica el número de partes iguales en
las que se divide el período de referencia que se tome (habitualmente el año).
Igualamos
C0 · (1 + n · i) = C0 · (1 + n·k · ik)
Y simplificando obtenemos la relación de equivalencia:
i = k · ik
Por tanto, los tantos de interés equivalentes en simple son proporcionales.
2.1.4 NÚMEROS COMERCIALES: CONCEPTO Y CÁLCULO
En el caso de una cuenta corriente bancaria es frecuente que, debido a los
movimientos de dinero, el capital (saldo) sea variable.
Cuando se da esta circunstancia, para calcular los intereses usamos los números
comerciales, siendo estos el producto del capital (saldo) por la duración de su
periodo:
Ni = Ci · ni
De esta forma los intereses de una cuenta corriente, con saldos Ci, podemos
calcularlos de la siguiente manera:
I = C1 · i ·n1 + C 2 · i ·n 2 + .... + C n · i ·n n = i·(C1 · n1 + C 2 · n 2 + .... + C n · nn )
Luego: I = i·(N1 + N2 + ... + Nn )
2.1.5 INTERÉS SIMPLE ANTICIPADO
El tipo interés simple es anticipado, y lo denotaremos i*, cuando los intereses son
prepagables, es decir, al principio del periodo.
La relación entre el tipo de interés simple anticipado ( i*) y el tipo de interés al
vencimiento ( i ) es la siguiente:
i* =
i
1+ i · n
fikai AULA FINANCIERA
, o bien, i =
i*
1- i* · n
13
2.2 Capitalización compuesta
Capítulo 2: Capitalización
2.2.1 DEFINICIÓN Y FÓRMULA GENERAL
Las operaciones en régimen de compuesta se caracterizan porque los intereses,
a diferencia de lo que ocurre en régimen de simple, a medida que se van
generando pasan a formar parte del capital de partida, se van acumulando, y
producen a su vez intereses en períodos siguientes (son productivos). En
definitiva, lo que tiene lugar es una capitalización periódica de los intereses. De esta
forma los intereses generados en cada período se calculan sobre capitales distintos
(cada vez mayores ya que incorporan los intereses de períodos anteriores).
ƒ CARACTERÍSTICAS DE LA OPERACIÓN:
Los intereses son productivos, lo que significa que:
• A medida que se generan se acumulan al capital inicial para producir nuevos
intereses en los períodos siguientes.
• Los intereses de cualquier período siempre los genera el capital existente al inicio de
dicho período.
ƒ DESARROLLO DE LA OPERACIÓN:
El capital al final de cada período es el resultado de añadir al capital existente al inicio
del mismo los intereses generados durante dicho período. De esta forma, la evolución
del montante conseguido en cada momento es el siguiente:
Momento 0: C0
Momento 1: C1 = C0 + I1 = C0 + C0 i = C0 · (1 + i)
Momento 2: C2 = C1 + I2 = C1 + C1 i = C1 · (1 + i) = C0 · (1 + i) · (1 + i) = C0 · (1 + i)2
Momento 3: C3 = C2 + I3 = C2 + C2 i = C2 · (1 + i) = C0 · (1 + i)2 · (1 + i) = C0 · (1 + i)3
Generalizando:
Cn = C 0 ·(1 + i)n
siendo (1+ i )n el factor de capitalización
Al igual que en capitalización simple, la duración (n) siempre ha de estar en la
misma unidad de tiempo que el tipo de interés (i).
Esta expresión:
-
Permite calcular el capital final o montante (Cn) en régimen de compuesta,
conocidos el capital inicial (C0), el tipo de interés (i) y la duración (n) de la
operación.
-
Es aplicable cuando el tipo de interés de la operación es constante. En caso
contrario habrá que trabajar con el tipo vigente en cada período.
14
fikai AULA FINANCIERA
ƒ CASO TIPO DE INTERÉS VARIABLE:
Si el tipo de interés es variable la expresión para obtener el capital final o montante
sería:
n
Cn = C 0 · ( 1 + i1 )·(1 + i2 )·(1 + i3 )...(1 + in ) = C 0 ·
∏(1 + i )
j
j =1
►EJEMPLO RESUELTO
Cálculo del montante en C.C. i = cte
Calcular el montante obtenido al invertir 200 euros al 5% anual durante 10 años en
régimen de capitalización compuesta.
Co = 200 €
C10= ?
0
10 años
i = 5% = 0,05
C10 = 200 · (1 + 0,05 )10 = 325,78 €
Si se hubiese calculado en simple:
C10 = 200 · (1 + 0,05 · 10) = 300 €
La diferencia entre los dos montantes (25,78 €) son los intereses producidos por los
intereses generados y acumulados hasta el final.
►EJEMPLO RESUELTO
Cálculo del montante en C.C. i = vble
Se quiere conocer qué capital podremos retirar dentro de 3 años si hoy colocamos
1.000 euros al 5% de interés anual compuesto para el primer año y cada año nos
suben el tipo de interés compuesto medio punto porcentual.
En este caso al ser el tipo de interés variable, para calcular el capital final, aplicaremos
la expresión:
n
Cn = C 0 · ( 1 + i1 )·(1 + i2 )·(1 + i3 )...(1 + in ) = C 0 ·
∏(1 + i )
j
j =1
C 3 = C 0 ·(1 + i1 )·(1 + i 2 )·(1 + i3 ) = 1000·(1 + 0,05)·(1 + 0,055 )·(1 + 0,06) = 1174,21 €
fikai AULA FINANCIERA
15
2.2.2 MAGNITUDES DERIVADAS
ƒ CÁLCULO DEL CAPITAL INICIAL:
Partiendo de la fórmula de cálculo del capital final o montante y conocidos éste, la
duración de la operación y el tanto de interés, bastará con despejar de la misma:
Cn = C0 · (1 + i)n
de donde se despeja C0:
C0 =
Cn
(1 + i)n
►EJEMPLO RESUELTO
Cálculo del capital inicial en C.C. i = cte
¿Cuánto deberé invertir hoy si quiero disponer dentro de 2 años de 1.500 euros para
comprarme un coche, si me aseguran un 6% de interés anual compuesto para ese
plazo?
Co = ?
Cn= 1500 €
0
2 años
i = 6% = 0,06
C0 =
Cn
(1 + i)
n
=
1500
(1 + 0,06) 2
= 1334,99 €
ƒ CÁLCULO DE LOS INTERESES TOTALES:
Conocidos los capitales inicial y final, se obtendrá por diferencia entre ambos:
I = Cn - C 0
En el caso de i = cte: I = C 0 ·(1 + i)n - C 0 = C 0 ·[ (1 + i)n - 1)
n
En el casi de i = vble I = C 0 ·
∏(1 + i j ) - C 0
j=1
►EJEMPLO RESUELTO
]
n
= C 0 · [ ∏(1 + i j ) - 1 ]
j=1
Cálculo de los intereses en C.C. i = cte
¿Qué intereses producirán 300 euros invertidos 4 años al 7% compuesto anual?
Calculamos primero el montante C4 = 300 (1 + 0,07)4 = 393,24 €
Luego, los intereses generados serán In = 393,24 – 300 = 93,24 €
16
fikai AULA FINANCIERA
ƒ CÁLCULO DEL TIPO DE INTERÉS:
Si se conoce el resto de elementos de la operación: capital inicial, capital final y
duración, basta con tener en cuenta la fórmula general de la capitalización compuesta
y despejar la variable desconocida.
Cn
= (1 + i)n
C0
Cn = C0 · (1 + i)n
n
►EJEMPLO RESUELTO
Cn
= (1 + i)
C0
i=n
Cn
-1
C0
Cálculo del tipo de interés en C.C. i = cte
Determinar el tanto de interés anual a que deben invertirse 1.000 euros para que en 12
años se obtenga un montante de 1.601,03 euros.
DATOS: Co = 1000 €
Calculamos i:
i=n
Cn = 1601,03 €
Cn
-1 =
C0
12
n = 12 años
1601,03
- 1 = 0,04 = 4%
1000
ƒ CÁLCULO DE LA DURACIÓN:
Por último, conociendo C0, Cn y el tipo de interés i, podemos calcular la duración:
Cn
= (1 + i)n
C0
Cn = C0 · (1 + i)n
log
Cn
= log(1 + i)n
C0
log C n log C 0
n=
log C n log C 0 = n·log(1 + i)
►EJEMPLO RESUELTO
log(1 + i)
Cálculo de la duración en C.C. i = cte
Un capital de 2.000 euros colocado a interés compuesto al 4% anual asciende a 3.202
euros. Determinar el tiempo que estuvo impuesto.
DATOS: Co = 2000 €
Cn = 3202 €
log C n log C 0
Calculamos n: n =
log(1 + i)
fikai AULA FINANCIERA
i = 4%
log 3202 log 2000
=
log(1 + 0,04)
= 12 años
17
2.2.3 TANTOS EQUIVALENTES EN CAPITALIZACIÓN COMPUESTA
La definición de tantos equivalentes es la misma que la vista en régimen de simple,
esto es, dos tantos cualesquiera, expresados en distintas unidades de tiempo,
son tantos equivalentes cuando aplicados a un mismo capital inicial y durante
un mismo período de tiempo producen el mismo interés o generan el mismo
capital final o montante.
En capitalización simple se comprobó que los tantos de interés equivalentes son
proporcionales, es decir, cumplen la siguiente expresión:
i = k · ik
Sin embargo, esta relación de proporcionalidad no va a ser válida en régimen de
compuesta, ya que al irse acumulando los intereses generados al capital de partida,
el cálculo de intereses se hace sobre una base cada vez más grande; por tanto,
cuanto mayor sea la frecuencia de capitalización antes se acumularán los intereses y
antes generarán nuevos intereses, por lo que existirán diferencias en función de la
frecuencia de acumulación de los mismos al capital para un tanto de interés dado.
Este carácter acumulativo de los intereses se ha de compensar con una aplicación de
un tipo más pequeño que el proporcional en función de la frecuencia de cómputo de
intereses. Todo esto se puede apreciar en el siguiente ejemplo, consistente en
determinar el montante resultante de invertir 1.000 euros durante 1 año en las
siguientes condiciones:
a) Interés anual del 12%
Cn = 1.000 x (1 + 0,12)1 = 1.120,00
b) Interés semestral del 6%
Cn = 1.000 x (1 + 0,06)2 = 1.123,60
c) Interés trimestral del 3%
Cn = 1.000 x (1 + 0,03)4 = 1.125,51
Los resultados no son los mismos, debido a que la capitalización de los intereses se
está realizando con diferentes frecuencias manteniendo la proporcionalidad en los
diferentes tipos aplicados.
Para conseguir que, cualquiera que sea la frecuencia de capitalización, el montante
final siga siendo el mismo es necesario cambiar la ley de equivalencia de los tantos.
RELACIÓN DE EQUIVALENCIA entre el tipo de interés anual ( i ) y el tipo de interés
efectivo fraccionado ( ik ):
El montante obtenido utilizando i :
y utilizando ik :
Cn = C0 · (1 + i)n
Cn = C0 · (1 + ik) n·k
donde k es la frecuencia de capitalización, que indica el número de partes iguales en
las que se divide el período de referencia que se tome (habitualmente el año).
Igualamos
18
C0 · (1 + i)n = C0 · (1 + ik) n·k
fikai AULA FINANCIERA
n
Simplificamos: (1 + i) = (1 + ik)
Despejando:
i = (1 + ik )k 1
n·k
(1 + i) = (1 + ik) k
, o bien, ik
= (1 + i)1/ k 1
ƒ TANTO NOMINAL:
El tanto nominal jk es un tipo de interés anual proporcional al tipo de interés efectivo
fraccionado ik en capitalización compuesta.
Cuando nos den el valor del tanto nominal jk, calcularemos el efectivo fraccionado de
la siguiente forma:
ik =
jk
k
►EJEMPLO RESUELTO
Tantos equivalentes en C.C. i = cte
Un capital de 2.000 euros se invierte durante 10 años al 4% anual nominal
devengando los intereses mensualmente. Determinar:
a) el tipo de interés efectivo mensual
b) el tipo de interés efectivo anual.
c) el montante al cabo de los 10 años.
DATOS: Co = 2000 €
a) i12 =
n = 10 años
j12 = 4%
j12 0,04
=
= 0,00333 = 0,33%
12
12
b) i = (1 + i12 )12 1 = ( 1 +
0,04 12
)
1 = 0,04074 = 4,074%
12
n
nK
c) C10 = C 0 ·(1 + i) = C 0 ·(1 + ik ) = 2000·( 1 +
0,04 120
) = 2981,66 €
12
►EJEMPLO RESUELTO
Tantos equivalentes en C.C. i = cte
Un capital de 5.000 euros se invierte durante 2 años y medio al 4% anual nominal
capitalizable trimestralmente. Determinar:
a) el tipo de interés efectivo trimestral.
b) el montante al final de la operación.
DATOS: Co = 5000 €
a) i 4 =
n = 2,5 años
j4 = 4%
j 4 0,04
=
= 0,01 = 1%
4
4
n
nK
b) C n = C 0 ·(1 + i) = C 0 ·(1 + ik ) = 5000·( 1 +
fikai AULA FINANCIERA
0,04 10
) = 5523,11 €
4
19
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 3. Descuento
3.1 Introducción
3.2 Descuento comercial simple
3.3 Descuento racional simple
3.3.1 Tipo de interés en las letras del tesoro
3.4 Descuento racional compuesto
3.4.1 Definición y fórmula general
3.4.2 Actualización periódica de los intereses
fikai AULA FINANCIERA
21
3.1 Introducción
Capítulo 3: Descuento
El descuento bancario es una operación de activo para las entidades financieras y uno
de los servicios bancarios de financiación a corto plazo más utilizados por las
empresas. La operación consiste en que la entidad financiera adelanta el importe de
un título de crédito no vencido (letra de cambio, pagaré, factura, recibo…),
descontando los intereses que corresponden por el tiempo que media entre la fecha
del anticipo y la fecha de vencimiento del crédito, las comisiones y demás gastos.
Las figuras que aparecen en la operación son: librador es la persona que emite el
documento, tenedor o tomador es la persona legitimada para cobrarlo y librado es la
persona obligada al pago.
En términos financieros, la entidad anticipa al cliente, el valor actual descontado de un
efecto comercial, y a vencimiento, el banco obtendrá el nominal. Se denomina
genéricamente efecto comercial a todo tipo de documento que evidencie que existe un
crédito a favor de la persona que lo posee, como consecuencia de la práctica habitual
de la empresa, contra otra que ha contraído dicha obligación o deuda.
Por tanto, las operaciones de descuento o de descapitalización son operaciones
financieras en las que se cambia un capital futuro por un capital presente, es decir, se
anticipa un capital (Cn,tn) hasta (Co,t0).
Al capital que figura en el documento (letra, factura, pagaré…) o capital futuro se le
denomina valor nominal (Cn).
El capital en el momento presente, se le llama valor actual, valor efectivo o valor
descontado (C0) .
La diferencia entre el valor nominal y el valor descontado es el descuento.
D = Cn – C0
El descuento depende, además de la cuantía del valor nominal, del tipo de interés
nominal aplicado y del tiempo.
Para el cálculo del descuento comercial en días se suele considerar el año comercial
de 360 días. Sin embargo, para operaciones de pasivo las entidades financieras
utilizan el año natural de 365 días.
Vamos a estudiar tres sistemas financieros de descuento:
1. Descuento comercial simple.
2. Descuento racional simple.
3. Descuento racional compuesto o actualización compuesta.
22
fikai AULA FINANCIERA
3.2 Descuento comercial simple
Capítulo 3: Descuento
El descuento comercial simple es el más utilizado en la práctica bancaria y se lleva a
cabo para periodos inferiores a un año.
Fórmula general del valor descontado: C0 = Cn ·(1 - n · i)
siendo (1-n·i) el factor de actualización.
Fórmula general del descuento: D = Cn
C 0 = Cn Cn ·(1 - n · i) = Cn · n · i
Donde: i = tipo de interés de descuento nominal = tanto de descuento nominal = d
Cn = valor nominal
C0 = valor descontado n = periodo de descuento
►EJEMPLO RESUELTO
Descuento comercial simple
Una entidad financiera descuenta una letra de cambio de 800 euros de nominal 80
días antes de su vencimiento. Sabiendo que el tipo de descuento nominal aplicado es
del 9% anual, se pide:
a) Valor del descuento realizado.
b) Valor descontado o efectivo que abona la entidad.
DATOS: Cn = 800 €
n = 80 días
a) D = Cn · n· i = 800 ·
d=i= 9%
80
· 0,09 = 16 €
360
b) C0 = Cn – D = 800 – 16 = 784 €
►EJEMPLO RESUELTO
Descuento comercial simple
Una entidad financiera descuenta una letra de cambio de 5000 euros de nominal
100 días antes de su vencimiento. Sabiendo que valor descontado o efectivo que
abona la entidad es 4785 €, calcular el tipo de interés nominal utilizado.
DATOS: Cn = 5000 €
n = 100 días
C0 = 4785 €
5000 4785
D = Cn · n · i
D
i=
=
= 0,1548 = 15,48%
5000 · 100 / 360
Cn · n
►EJEMPLO PROPUESTO
Descuento comercial simple
Una entidad financiera descuenta una letra de cambio de 1500 euros de nominal
90 días antes de su vencimiento. Sabiendo que el tanto de descuento es del 8% anual,
que la comisión del 0,5% y que los impuestos ascienden a 30 euros, calcular el valor
efectivo de la letra.
fikai AULA FINANCIERA
23
3.3 Descuento racional simple
Capítulo 3: Descuento
Fórmula general del valor descontado:
Partimos de la capitalización simple: Cn = Co · ( 1 + n · i )
y despejamos el valor de C0 , que sería el valor descontado: C 0 =
siendo
Cn
(1 + n · i)
1
el factor de actualización.
(1 + n · i)
Fórmula general del descuento: D = C n
C 0 = Cn
Cn
Cn · n ·i
=
(1 + n · i) (1 + n · i)
3.3.1 TIPO DE INTERÉS EN LAS LETRAS DEL TESORO
Las Letras del Tesoro son títulos de Deuda Pública emitidos por el Estado para su
financiación. Su plazo de vencimiento suele ser inferior a 18 meses, su valor nominal
es de 1.000 euros y presentan la peculiaridad de que se emiten al descuento. Es
decir, el suscriptor al comprar paga menos que el valor nominal del título, mientras que
en el momento del vencimiento recibe dicho valor nominal. Este menor precio en el
momento de la compra es la rentabilidad que ofrece el título. De esta manera, el
capital invertido será el precio pagado por la letra adquirida y los intereses que se
obtienen serán la diferencia entre ese precio de adquisición y el precio que se
obtenga por la letra cuando se venda o cuando se amortice (1.000 euros).
Para calcular la rentabilidad que obtiene el inversor hay que distinguir entre Letras con
vencimiento a menos de 1 año y a más de 1 año:
a) Si se emiten a plazos inferiores o iguales a los 12 meses:
•
Se calculan aplicando las fórmulas del descuento racional simple.
•
Las emitidas a 12 meses (o 52 semanas) tienen una vida exacta de 364
días.
b) Si se emiten a 18 meses:
•
24
Se aplican las fórmulas del descuento racional compuesto.
fikai AULA FINANCIERA
►EJEMPLO RESUELTO
Descuento racional simple
Las Letras del Tesoro a 12 meses se adjudicaron a un tipo de interés marginal del
2,975%. ¿Cuál es el precio marginal de la subasta o precio mínimo aceptado?
DATOS: Valor nominal = Cn = 1.000 €
d = n° de días = 364
Utilizamos la ley de descuento racional simple: C 0 =
C0 = P =
1.000
364
· 0,02975
1+
360
i = 2,975%
Cn
(1 + n · i)
= 970,79 euros
►EJEMPLO RESUELTO
Descuento racional simple
El importe que se abonó por una Letra del Tesoro a 12 meses fue de 980,75 euros.
Calcula el tipo de interés de la subasta.
DATOS: Valor nominal = Cn = 1.000 €
d = n° de días = 364
Utilizamos la ley de descuento racional simple: C 0 =
Sustituimos: 980,75 =
P = C0 = 980,75 €
Cn
(1 + n · i)
1000
y despejamos i = 0,01941 = 1,941%
364
· i)
(1 +
360
►EJEMPLO RESUELTO
Descuento racional simple
Un capital de 5000 euros se descuenta 30 días antes de su vencimiento a un 7%
anual. Calcular el descuento racional simple y el descuento comercial simple.
DATOS: Valor nominal = Cn = 5000 €
d = n° de días = 30
i = 7%
30
· 0,07
Cn · n · i
360
=
= 29 €
Descuento racional simple: D =
30
(1 + n · i)
(1 +
· 0,07)
360
5000 ·
Descuento comercial simple: D = C n · n · i = 5000 ·
fikai AULA FINANCIERA
30
· 0,07 = 29,17 €
360
25
3.4 Descuento racional compuesto
Capítulo 3: Descuento
3.4.1 DEFINICIÓN Y FÓRMULA GENERAL
En esta ley financiera el descuento se calcula sobre el valor del capital actualizado al
inicio de cada periodo.
Fórmula general del valor descontado:
Partimos de la capitalización compuesta: Cn = C0 · (1 + i)
n
y despejamos el valor de C0 , que sería el valor descontado: C 0 =
Siendo
1
(1 + i)n
Cn
(1 + i)n
el factor de actualización
Fórmula general del descuento: D = C n
C 0 = Cn
►EJEMPLO RESUELTO
Cn
(1 + i)
n
= Cn · ( 1
1
(1 + i)n
)
Descuento racional compuesto
Sea un capital de 5000 euros que vence dentro de 10 años. Calcular el valor
descontado y el descuento utilizando la ley de actualización compuesta, siendo el tipo
de interés el 5% nominal anual.
DATOS: Valor nominal = Cn = 5000 €
Valor descontado: C 0 =
Cn
(1 + i)
n
=
duración = 10 años
5000
(1 + 0,05)10
i = 5%
= 3069,57 €
Descuento = Cn – C0 = 5000 – 3068,57 = 1930,43 €
3.4.2 ACTUALIZACIÓN PERIÓDICA DE LOS INTERESES
►EJEMPLO PROPUESTO
Descuento racional compuesto
Sea un capital de 5000 euros que vence dentro de 3 años y medio. Calcular el valor
actual de dicho capital siendo el tipo de interés un 6% nominal actualizable
semestralmente.
26
fikai AULA FINANCIERA
►CUESTIONARIO
Capítulos 1- 3: CAPITALIZACIÓN Y DESCUENTO
1. ¿Cuánto vale una Letra del Tesoro, en tanto por ciento de nominal, si calculamos su
valor al 3% de interés y faltan 45 días para su vencimiento?
A)
B)
C)
D)
97,20 %
99,63 %
98,30 %
100 %
2. Si se realiza un ingreso de 9.000 euros a plazo fijo durante 5 años al 4% nominal anual.
Los intereses se abonan trimestralmente y se reinvierten ¿Cuál es el saldo final de la
operación?
A)
B)
C)
D)
10.981,71 €
11.025,85 €
10.949,87 €
10.988,97 €
3. Si adquiriese Letras del Tesoro a 1 año (exactamente a 360 días en base a 360) por
946€, siendo su valor nominal 1.000€ ¿qué rentabilidad obtendría en cada una de las
Letras a 1 año?
A)
B)
C)
D)
5,400%
5,708%
5,630%
5,880%
4. Nos ofrecen un depósito en el que se estima una rentabilidad nominal anual del 6% y
que trimestralmente abonan los intereses al depósito. Si decidimos aportar 12.000 euros,
¿Cuál será el capital dentro de 4 años?
A)
B)
C)
D)
15.309,86 €
15.227,83 €
15.149,72 €
15.245,87 €
5. En una inversión financiera a un año y a efectos de conseguir la mejor rentabilidad al
finalizar la operación, ¿Cuál de las siguientes operaciones escogería, suponiendo que
las condiciones de la operación se mantengan durante todo el año?
A)
B)
C)
D)
Interés nominal del 4,15% pagadero anualmente.
Interés nominal del 4,05% pagadero bimestralmente.
Interés nominal del 4,10% pagadero trimestralmente.
Interés nominal del 4,07% pagadero mensualmente.
6. En las operaciones de capitalización:
A)
B)
C)
D)
Se adelanta el cobro de un capital.
Se retrasa la disponibilidad de un dinero.
Se realiza un descuento sobre el valor nominal.
Se generan intereses que se van acumulando siempre al capital inicial.
7. Si depositamos un capital de 5.000 € ¿Qué capital final obtendremos, si dicha
imposición es a un plazo de 6 meses y es remunerada al 3% anual?
A)
B)
C)
D)
5.075 €
5.070 €
75 €
Ninguna de las anteriores.
fikai AULA FINANCIERA
27
8. Una empresa descuenta una letra de 6.000,00€ que vence dentro de 90 días. La entidad
bancaria abona por la Letra 5.855 €. Calcula el tipo de interés nominal que aplica la
entidad, suponiendo que no existen gastos.
A)
B)
C)
D)
9,67 %
10 %
8,32 %
Ninguna de las anteriores.
9. Sabiendo que el tipo de interés nominal resultante en una subasta de Letras del
Tesoro a 12 meses es 3,645%, calcular el valor efectivo de dicha Letra.
A)
B)
C)
D)
35,55 €
964,45 €
963,55 €
96,445 €
10. ¿Qué capital hay que colocar al 4% de interés nominal anual para obtener, al cabo de
cuatro años, otro de 10.000 €? Se supone que el abono de intereses es trimestral y se va
acumulando al capital inicial.
A)
B)
C)
D)
8.528,21 €
1.471,78 €
8.874,49 €
5.339,08 €
11. Un depósito a plazo de 3 años permite recuperar al inversor 10.500 € por cada 9.000 €
de inversión. Calcula el tipo de interés nominal de dicho depósito, sabiendo que los
intereses se generan cada semestre y se acumulan al capital.
A)
B)
C)
D)
8,01 %
5,20 %
10,54 %
5,50 %
12. En una operación de actualización a interés compuesto, el valor efectivo disminuye a
medida que se hace menor:
A)
B)
C)
D)
La duración de la operación.
El tipo de interés nominal.
La frecuencia anual de actualización.
Ninguna es cierta.
13. Calcular el tipo de interés nominal anual que se está aplicando en un bono cupón
cero a 10 años, con cálculo semestral de intereses, si por un nominal de 1.000 € se
deben pagar 610 €.
A)
B)
C)
D)
6%
4%
5%
Ninguna de las anteriores.
14. El tipo de interés nominal de una imposición a plazo de 3 años es el 4% si los
intereses se acumulan mensualmente al capital. Calcular el tipo de interés efectivo anual
correspondiente.
A)
B)
C)
D)
4%
4,07 %
3,33%
6,01 %
28
fikai AULA FINANCIERA
15. Un depósito a plazo ofrece un 5% de interés anual nominal con acumulación
trimestral de intereses. Por un capital inicial de 8.000 €, a los dos años y tres meses
obtendrá un capital final de:
A)
B)
C)
D)
8.952,58 €
8.928,24 €
8.900 €
8.946,34 €
16. Una operación de inversión de 25.000 € a cuatro años al 3,75% nominal con
capitalización mensual obtendrá un capital final de:
A)
B)
C)
D)
29.039,06 €
28.750,00 €
21.522,74 €
29.045,86 €
17. En una operación en que se descuenta un efecto comercial de nominal 6.000 € y
vencimiento a los 60 días a una tasa de descuento del 5% anual, el valor efectivo a
percibir es, suponiendo que se aplica la fórmula del descuento simple comercial:
A)
B)
C)
D)
5.700 €
5.950 €
5.850 €
Ninguna de las anteriores
18. En la misma operación de la pregunta anterior, ¿qué valor efectivo se percibirá si el
descuento es por modalidad matemática o racional?
A)
B)
C)
D)
5.700,00 €
5.950,00 €
5.950,41 €
Ninguna de las anteriores.
19. A que tipo de interés habría que invertir un capital hoy para que se duplique en 10
años:
A)
B)
C)
D)
6,25 %
5,53 %
7,18 %
8,11 %
20. En una operación financiera de 1 año, el tipo de interés a vencimiento es del 3%,
¿cuál es el tipo de interés simple anticipado?
A)
B)
C)
D)
3,09 %
3%
2,91 %
Ninguna de las anteriores.
21. Un cliente abre una cuenta corriente bancaria ingresando 3000 €. El tipo de interés
anual simple es del 4%. Al cabo de 10 días ingresa otros 1000 € más y 40 días después
retira 500 €. Si 30 días después la entidad financiera liquida los intereses, ¿cuál será su
importe?
A)
B)
C)
D)
11800 €
32,33 €
6,03 €
Ninguna de las anteriores.
fikai AULA FINANCIERA
29
22. ¿Cuál es el criterio para aplicar la ley simple o la compuesta en las operaciones de
capitalización?
A)
B)
C)
D)
El plazo.
La frecuencia de pago de intereses.
La reinversión de intereses.
No existe ningún criterio.
23. ¿Cual es el criterio para la aplicación de la ley simple o la compuesta en operaciones
de descuento?
A)
B)
C)
D)
El plazo.
La frecuencia de pago de intereses.
La reinversión de intereses.
No existe ningún criterio.
30
fikai AULA FINANCIERA
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 4. Tipos de interés y rentabilidad
4.1 Tipos de interés
4.1.1 Tasa nominal y efectiva en interés compuesto
4.1.2 Tipos de interés spot y forward
4.2 Rentabilidad
4.2.1
4.2.2
4.2.3
4.2.4
4.2.5
4.2.6
Rentabilidad nominal y real
Rentabilidad Simple
Tasa Anual Equivalente (TAE)
Tasa Interna de Rentabilidad (TIR)
Tasa de Rentabilidad Efectiva (TRE)
Tasa Geométrica de Rentabilidad (TGR)
fikai AULA FINANCIERA
31
4.1 Tipos de interés
Capítulo 4: Tipos de interés y rentabilidad
4.1.1 TASA NOMINAL Y EFECTIVA EN INTERÉS COMPUESTO
El tanto nominal jk es un tipo de interés anual proporcional al tipo de interés efectivo
fraccionado ik en capitalización compuesta.
Por tanto, la relación entre el tanto nominal capitalizable k-esimalmente jk y el tanto
efectivo k-esimal es:
ik =
jk
k
donde k es la frecuencia de capitalización.
Como vimos en el capítulo 2, el tipo efectivo anual compuesto = i = (1 + ik )k
1
Luego sustituyendo:
Tipo efectivo anual compuesto
i = ( 1+
jk k
) -1
k
y despejando jk en función de i :
Tanto nominal
jk = k · [
1
(1 + i) k
-1
]
Si k >1 el tipo de interés efectivo anual (i) es mayor que el tanto nominal (jk)
Si k = 1, entonces i = j1
►EJEMPLO RESUELTO
Tanto nominal y tanto efectivo
Calcular el tipo de interés efectivo anual correspondiente a una operación de
capitalización al 10% nominal pagadero semestralmente.
DATOS: Tanto nominal pagadero semestralmente = j2 = 10%
SE PIDE: Tanto efectivo anual = i
Utilizamos la expresión: i = ( 1 +
i = ( 1+
32
j2 2
0,10
) - 1= ( 1+
2
2
)2
jk k
) - 1 para k = 2
k
1 = 0,1025 = 10,25% >10% = j2
fikai AULA FINANCIERA
4.1.2 TIPOS DE INTERÉS SPOT Y FORWARD
Las operaciones al contado se liquidan a un tipo de interés al contado o “spot” y las
operaciones a plazo, es decir, contratadas en una fecha pero materializadas en una
fecha futura, se liquidan a un tipo de interés a plazo o “forward”.
Para vencimientos superiores al año se aplica el interés compuesto, y para
vencimientos inferiores a un año el interés simple.
La curva de tipos de interés o curva de rendimientos (yield curve) es la
representación gráfica en un eje de coordenadas, de los tipos spot observados en el
mercado (eje vertical) asociadas a los vencimientos de los activos (eje horizontal); en
un momento dado.
La Estructura Temporal de los Tipos de Interés (ETTI) es la curva construida con
los tipos de interés correspondientes a los bonos cupón cero sin riesgo. Esta curva nos
proporciona hoy las expectativas sobre la evolución de tipos futuros, es decir, si la
expectativa es de evolución de tipos al alza (curva ascendente), a la baja (curva
descendente) o de no variación (curva plana).
►EJEMPLO RESUELTO
Tipo de interés spot
Calcular el tipo spot correspondiente a una operación financiera de duración 2 años,
siendo el nominal del activo 1000 euros y el valor efectivo hoy 910,55 euros.
DATOS: Valor nominal = Cn = 1000 € Valor efectivo = C0 = 910,55 €
n = 2 años
El vencimiento del activo financiero es superior al año, luego utilizaremos interés
compuesto:
Cn = C0 · (1+i)n
sustituyendo: 1000 = 910,55 · (1+i)2
Y despejando: tipo spot asociado al plazo de 2 años = i = 0,0479 = 4,79%
►EJEMPLO RESUELTO
Tipo de interés forward
Sean dos activos A y B, el primero con un rendimiento del 6% a 1 año y el B con un
rendimiento del 7% a dos años. ¿Cuál será el tipo forward o implícito para una
inversión a un año, dentro de un año?
iforward = ?
iA = 6%
0
1
2
iB = 7%
Planteamos la siguiente igualdad:
(1 + i A )1·(1 + i forward )1 = (1 + iB ) 2
Sustituimos
(1 + 0,06)1·(1 + i forward )1 = (1 + 0,07) 2 y despejamos i forward = 0,08 = 8%
fikai AULA FINANCIERA
33
4.2 Rentabilidad
Capítulo 4: Tipos de interés y rentabilidad
4.2.1 RENTABILIDAD REAL
La rentabilidad real de una inversión considera, además de la rentabilidad financiera,
otras variables tales como la fiscalidad, los gastos de gestión, las comisiones y la tasa
de inflación.
Para calcular la rentabilidad real, teniendo en cuenta estas variables, utilizaremos la
siguiente expresión:
(1 + rREAL ) · (1 + Π ) = (1 + rFF )
Así pues, rREAL =
1 + rFF
1+ Π
siendo
rREAL = La rentabilidad real
Π = La tasa de inflación
rFF = La rentabilidad financiero fiscal
1
►EJEMPLO RESUELTO
Rentabilidad REAL
Calcular la rentabilidad real de una inversión que ha tenido una rentabilidad financierofiscal del 4%, siendo la tasa de inflación del 4,5%.
DATOS:
rFF = 4%
Π = 4,5%
SE PIDE:
rREAL = ?
Para calcular la rentabilidad real utilizamos la expresión :
rREAL =
1 + rFF
1+ Π
1=
1 + 0,04
- 1 = - 0,0048 = - 0,48 % Rentabilidad real negativa.
1 + 0,045
►EJEMPLO PROPUESTO
Rentabilidad REAL
Calcular la tasa de inflación sabiendo que una inversión que ha tenido una rentabilidad
financiero-fiscal del 6% y una rentabilidad real del 3%.
34
fikai AULA FINANCIERA
4.2.2 RENTABILIDAD SIMPLE ( RS )
La expresión para determinar la rentabilidad simple RST es:
RS T =
PT + D T - P0
P0
donde
PT:precio del título al final del periodo T
DT:suma de los ingresos percibidos durante el periodo T
P0:precio del título al inicio del periodo
La rentabilidad simple supone que los dividendos y otros rendimientos se perciben al
final del periodo, o que se reinvierten a una tasa del 0% si se perciben antes.
►EJEMPLO RESUELTO
Rentabilidad simple
Hace dos años se adquirieron acciones de una compañía, siendo su cotización 15€.
Calcular la rentabilidad simple de cada uno de los dos años de una acción, sabiendo
que su cotización al final del primer año fue 18€ y al final del segundo año 17,1€.
15€
18€
0
1
17,1€
2
Para conocer en qué porcentaje se ha revalorizado anualmente la acción calculamos
la rentabilidad simple:
RS1 =
18 - 15
= 20%
15
►EJEMPLO PROPUESTO
RS 2 =
17,1 - 18
= - 5%
18
Rentabilidad simple
Hace 6 meses compramos 100 acciones a 35 €/acción, pagando 44 € de comisión y
hoy la acción cotiza a 36,50€. Calcular la rentabilidad simple de la acción, sabiendo
que hace 3 meses se cobró un dividendo de 1,20 € por acción.
fikai AULA FINANCIERA
35
4.2.3 TASA ANUAL EQUIVALENTE ( TAE )
El Banco de España, obliga a todas las entidades financieras a incluir este índice
desde el año 1990, en que publica la norma 8/1990 sobre “Transparencia de las
operaciones y protección de la clientela”.
El significado exacto es Tasa Anual Equivalente o Tasa Anual Efectiva. Es un
indicador que, en forma de tanto por ciento anual, revela el coste o rendimiento
efectivo de un producto financiero, ya que incluye el interés y los gastos y
comisiones bancarias.
Así, si una operación financiera no tiene comisiones ni gastos, su TAE coincidiría con
el tipo de interés efectivo anual.
La TAE se calcula de acuerdo con una fórmula matemática estandarizada que tiene en
cuenta el tipo de interés nominal de la operación, la frecuencia de los pagos
(mensuales, trimestrales, etc.), las comisiones y algunos gastos de la operación. En el
caso de los créditos, no se incluyen en el cálculo del coste efectivo algunos
conceptos, como los gastos que el cliente pueda evitar en uso de las facultades que
le concede el contrato, los gastos a abonar a terceros o los gastos por seguros o
garantías (salvo que la entidad imponga su suscripción para la concesión del crédito).
La TAE es muy útil porque permite comparar distintos productos u opciones de
inversión, con independencia de sus condiciones particulares. Esto es así
especialmente entre productos de igual naturaleza, en los que los restantes
elementos, y en particular el riesgo que tienen, son idénticos.
Las entidades están obligadas a informar sobre la TAE de sus operaciones en la
publicidad que hagan de sus productos, en los contratos que formalicen con sus
clientes, en las ofertas vinculantes que realicen y en los documentos de liquidación
de operaciones activas y pasivas.
►EJEMPLO RESUELTO
TAE
Un cliente solicita un préstamo por 4.000 € que debe devolver a final de año en un sólo
pago que comprende el capital más los intereses (calculados mensualmente). El tipo
de interés nominal del préstamo es del 6% y la entidad financiera deduce los gastos de
gestión, por lo que realmente se entrega al cliente 3.950 €. Calcular la TAE.
Primero calculamos la contraprestación en t=1 (devolución del capital más intereses,
siendo j12 = 6%):
n
12
Contraprestación = C1 = C 0 ·(1 + i) = P·(1 + i12 )
⎛ 0,06 ⎞
= 4000·⎜1 +
⎟
12 ⎠
⎝
12
= 4246,71 €
Y a continuación, calculamos la TAE planteando la siguiente equivalencia financiera:
3950 =
36
4246,71
1 + TAE
Despejando: TAE = 7,51%
fikai AULA FINANCIERA
4.2.4 TASA INTERNA DE RENTABILIDAD ( TIR )
La Tasa Interna de Retorno o Tasa Interna de Rentabilidad (TIR) de una inversión,
está definida como la tasa de interés con la cual el valor actual neto o valor presente
neto (VAN o VPN) es igual a cero.
El VAN o VPN es calculado a partir de los flujos positivos y negativos de capital,
trasladando todas las cantidades futuras al presente.
La expresión que permite calcular el VAN es:
N
VAN =
D0 +
Qj
∑(1 + i)
j
j =1
Donde:
VAN = Valor Actual Neto.
Do = Desembolso inicial.
Qj = Flujo de Caja en el periodo j.
i = tasa de descuento o actualización
La obtención del VAN constituye una herramienta fundamental para la evaluación y
gerencia de proyectos, así como para la administración financiera.
La Tasa Interna de Retorno (TIR) es el tipo de descuento que hace igual a cero el
VAN. Así pues, para calcular la TIR plantearemos la siguiente ecuación:
N
D0 +
∑(1 +QTIR)
i
i
=0
TIR
i =1
Esta tasa interna de rentabilidad TIR corresponde a la rentabilidad del inversor,
asumiendo que los flujos periódicos se reinvierten a una tasa igual a la TIR.
►EJEMPLO RESUELTO
Cálculo de la TIR
Un cliente adquirió 2.000 participaciones de un fondo de inversión que cotizaban a 4 €.
Al cabo de un año vendió 600 participaciones que en ese momento cotizaban a 5 €.
Si al cabo de dos años la cotización de la participación del fondo es de 6 €, calcular la
TIR de esta inversión.
El desembolso inicial de la inversión = Do = 2.000 · 4 = 8.000 €
En t = 1, cobra Q1 = 600 · 5 = 3.000 €
En t = 2, cobra Q2 = 1.400 · 6 = 8.400 €
Para calcular la TIR de este flujo de cobros y pagos planteamos la siguiente ecuación:
N
D0 +
∑(1 +QTIR)
i
i
=0
i =1
fikai AULA FINANCIERA
8.000 +
3.000
1
(1 + TIR )
+
8.400
(1 + TIR ) 2
=0
TIR = 22,92%
37
4.2.5 TASA DE RENTABILIDAD EFECTIVA ( TRE )
En el cálculo de la Tasa de Rentabilidad Efectiva (TRE) se considera que un capital
cobrado puede reinvertirse al tipo de interés vigente.
Para calcular la TRE:
Primero, calculamos el montante (Cn) de la inversión capitalizando los flujos de caja al
tipo de interés correspondiente.
A continuación, planteamos la siguiente ecuación:
C n = C 0 ·(1 + TRE)n y despejamos la tasa TRE
TRE = n
Cn
C0
1
Si el tipo de interés de reinversión es menor que la TIR Î TRE < TIR
Si el tipo de interés de reinversión es mayor que la TIR Î TRE > TIR
►EJEMPLO RESUELTO
Cálculo de la TRE
¿Cuál ha sido la rentabilidad efectiva de la siguiente operación si suponemos que el
inversor reinvierte los cupones anuales y amortiza el bono a vencimiento?
Compra:
Vencimiento:
Cupón anual:
Valor nominal:
TIR de adquisición:
Precio de compra:
15-05-2001
15-05-2005
4,5%
1.000 €
6,25%
93,97%
Tipos de interés a un año
15-05-2001:
3,50%
15-05-2002:
3,80%
15-05-2003:
4,70%
15-05-2004:
5,25%
Primero calculamos el valor final de los cupones percibidos y del nominal a
vencimiento utilizando los tipos de interés dados:
Cn=45·(1+0,038)·(1+0,047)·(1+0,0525)+45·(1+0,047)·(1+0,0525)+45·(1+0,0525)+1045=
= 1193,42 €
A continuación, planteamos la siguiente ecuación:
C n = C 0 ·(1 + TRE )n
y sustituyendo: 1193,42 = 939,7 · (1+TRE)4
Despejando la tasa de rentabilidad efectiva: TRE = 0,06157 = 6,16 % < TIR ya que los
tipos de interés de reinversión han sido inferiores a la TIR.
38
fikai AULA FINANCIERA
4.2.6 TASA GEOMÉTRICA DE RENTABILIDAD ( TGR )
La Tasa Geométrica de Rentabilidad (TGR) (Time-weighted rate of return) es la
rentabilidad del gestor de la cartera y se calculará realizando la media geométrica de
las rentabilidades simples de los diferentes periodos.
Para ello seguiremos los siguientes pasos:
Primero, determinamos las rentabilidades simples para cada subperiodo de inversión.
A continuación, planteamos la igualdad:
(1 + TGR)n = (1 + RS1 )·(1 + RS 2 )·...·(1 + RSn )
Y por último despejamos la TGR:
TGR = n (1 + RS1 )·(1 + RS 2 )·...·(1 + RSn )
1
Esta es la rentabilidad que mide sólo la actuación del gestor quitando la influencia de
las decisiones del inversor de aportar o retirar fondos de la cartera.
Comparando la TIR y la TGR se puede analizar el grado de acierto de la política de
entradas y salidas de capital de la inversión llevada a cabo:
▪ Si TIR > TGR, el inversor ha acertado en sus decisiones.
▪ Si TIR = TGR, el resultado es indiferente de la política llevada a cabo.
▪ Si TIR < TGR, el inversor se ha equivocado en su política.
►EJEMPLO RESUELTO
Cálculo de la TGR
Un gestor aconsejó a un inversor adquirir participaciones de un fondo de inversión que
cotizaban a 4 €.
Al cabo de un año las participaciones cotizan a 6 € y a los dos años cotizan a 5 €.
Calcular la tasa geométrica de rentabilidad.
Primero, determinamos las rentabilidades simples para cada año:
RS1 =
6-4
= 0,5 = 50%
4
RS 2 =
5-6
= - 0,1667 = - 16,67%
6
A continuación, planteamos la igualdad:
(1 + TGR) 2 = (1 + RS1 )·(1 + RS 2 ) = (1+0,50)·(1-0,1667) = 1,25
Por último, despejamos: TGR =
►EJEMPLO PROPUESTO
1
2
(1,25)
- 1 = 11,8 %
Cálculo de la TGR
La rentabilidad anual de una cartera ha sido la siguiente: 1er año: 14%, 2° año: 19%,
3er año: -10% y 4° año: 14%. Calcular la rentabilidad geométrica anual de la cartera
durante estos 4 años.
fikai AULA FINANCIERA
39
►CUESTIONARIO
Capítulo 4: TIPOS DE INTERÉS Y RENTABILIDAD
1. Sean dos activos A y B, el primero con un rendimiento del 8% a 1 año y el B con un
rendimiento del 10% a dos años. ¿Cuál será el tipo forward o implícito para una inversión
a un año, dentro de un año?
A)
B)
C)
D)
El 10%
El 12%
El 11,5%
Ninguno de los anteriores.
2. La rentabilidad efectiva de un bono es mayor que su TIR cuando:
A)
B)
C)
D)
El tipo de interés es superior a su TIR.
El tipo de interés es inferior a su TIR.
El tipo de interés es igual a su TIR.
Ninguna de las anteriores.
3. La TAE de una operación sin comisiones que rinde un 4% nominal acumulable
trimestralmente es:
A)
B)
C)
D)
4%
1%
4,074%
4,06%
4. Una entidad bancaria oferta una póliza de ahorro al 5,35% TAE. ¿Cuál es el interés
nominal aplicado, si el abono de intereses es trimestral?
A)
B)
C)
D)
5,22%
5,25%
5,46%
5,35%
5. Para calcular el coste o la rentabilidad de una operación financiera teniendo en cuenta
la frecuencia de capitalización o descuento y también los gastos y comisiones, se utiliza:
A)
B)
C)
D)
Tipo de interés nominal.
Tipo de interés efectivo.
TAE.
Ninguno de los anteriores.
6. Indica cuál de las siguientes afirmaciones es correcta:
A) La TAE siempre es superior al tipo de interés nominal.
B) La TAE la definen, para cada operación, las propias entidades financieras estableciendo los
criterios para su cálculo.
C) La TAE tiene en cuenta todos los gastos de una operación.
D) La TAE puede coincidir, en algún caso, con el tipo de interés efectivo.
7. La TAE de una operación sin comisiones que rinde un 3% nominal acumulable
bimestralmente es:
A)
B)
C)
D)
3,0000 %
3,0225 %
3,0378 %
0,5000 %
40
fikai AULA FINANCIERA
8. Una persona compra unas acciones por 6.250 €. Al cabo de 1 año recibe unos
dividendos de 180 €, y a los 2 años de 240 €. Si vende las acciones a los 3 años por
7.500€ y paga en ese momento 40 € en concepto de gastos, la ecuación que permite
determinar la TIR, i, de la inversión es:
A)
B)
C)
D)
180
(1+i)
180
(1+i)
180
(1+i)
180
(1+i)
+
+
+
+
240
(1+i)
2
240
(1+i)
2
240
(1+i)
2
240
(1+i)
2
+
+
7.540
(1+i)
3
7.460
(1+i)
+
=
3
= 6.250
= 6.250
7.500
(1+i)
= 6.210
3
7.540
(1+i)
3
+ 6.250
9. En un préstamo hipotecario sin comisión de apertura que cobra una comisión de
cancelación del 1% y cuya tasa de interés nominal es del 6% liquidable mensualmente la
Tasa Anual Equivalente será:
A)
B)
C)
D)
5%
6%
6,17 %
6,37 %
10. Un cliente solicita a una entidad financiera un crédito por un importe de 4.000 € que
debe devolver al final de año en un solo pago que comprende el capital más los
intereses, calculados mensualmente. El crédito tiene un tipo de interés nominal del 6% y
la entidad deduce gastos de gestión, por lo que, en lugar del nominal del crédito, entrega
al cliente 3.950 €. La TAE de la operación es:
A) 6,51 %
B) 6,17 %
C) 6 %
D) 7,51 %
11. Si las rentabilidades obtenidas por un fondo de inversión durante los últimos 3 años
han sido, respectivamente, 8’12%, - 3’23% y 5’80%, la tasa geométrica de rentabilidad será:
A)
B)
C)
D)
10,69 %
3,26 %
5,34 %
3,45 %
12. ¿Cuál será la rentabilidad real de una inversión que ha tenido una rentabilidad
financiero-fiscal del 8% y una tasa de inflación del 4%?
A)
B)
C)
D)
4%
3,265 %
3,846 %
3,455 %
13. ¿Cuál es la TIR de un proyecto cuya inversión es de 1.000 € y los flujos de caja son
de 300 € (año 1), 400 € (año 2) y 500 € (año 3)?
A)
B)
C)
D)
20 %
8’90 %
12’50 %
9’18 %
fikai AULA FINANCIERA
41
14. Si ésta es la situación del mercado interbancario de depósitos del Euribor:
Tipos
Tipos
Tipos
Tipos
Tipos
Tipos
a
a
a
a
a
a
1
2
3
6
9
12
mes
meses
meses
meses
meses
meses
2’25 %
2’27 %
2’30 %
2’41 %
2’53 %
2’66 %
¿Qué previsión está haciendo el mercado de cómo van a estar los tipos de interés para
el plazo de 3 meses de hoy en 6 meses?
A)
B)
C)
D)
2’630 %
2’506 %
2’737 %
Ninguna de las anteriores.
15. ¿Qué es la TIR?
A) La tasa de rentabilidad que se va a conseguir en cualquier tipo de inversión,
independientemente del tipo de reinversión.
B) La tasa anual equivalente a una operación de tipo de interés simple, pero sólo el interés es
pospagable o vencido e inmediato.
C) La tasa de actualización que hace que el VAN de una inversión sea cero.
D) La tasa nominal de una inversión.
16. ¿Cuál será la rentabilidad geométrica anualizada de una inversión que genera los
siguientes flujos de caja anuales?
Años
1
2
3
A)
B)
C)
D)
Inicio
de
inversión
200 €
250 €
350 €
la Fin
de
inversión
250 €
350 €
400 €
la
26,40%
18,37%
66,67%
25,99%
17. Una persona compra unas acciones por 6.250 €. Al cabo de 1 año recibe unos
dividendos de 180 €, y a los 2 años de 240 €. Si vende las acciones a los 3 años por
7.500 € y paga en ese momento 40 € en concepto de gastos y considerando que los
dividendos se reinvierten a una tasa del 1’5% anual, la tasa de rentabilidad efectiva de la
operación, expresada en término anual, es:
A)
B)
C)
D)
6,077 %
8,742 %
6,453 %
8,072 %
18. Si la TIR de una cartera en el último semestre ha sido del 8% y la TGR del 13%,
podemos concluir que:
A) El inversor se ha equivocado en la elección de los momentos de compra y venta de los
activos de la cartera.
B) El inversor ha acertado en la elección de los momentos de compra y venta de los activos de
la cartera.
C) El inversor ha acertado en la selección de los títulos que forman la cartera.
D) El inversor se ha equivocado en la selección de los títulos que forman la cartera.
42
fikai AULA FINANCIERA
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 5. Conceptos estadísticos
5.1 Media y esperanza
5.1.1 Definiciones básicas
5.1.2 Media muestral y esperanza matemática
5.2 Varianza y desviación típica
5.3 Covarianza y correlación
5.4 Regresión lineal mínimo cuadrática
5.4.1 Línea Característica de un Título (LCT)
fikai AULA FINANCIERA
43
5.1 Media y Esperanza
Capítulo 5: Conceptos estadísticos
5.1.1 DEFINICIONES BÁSICAS
En todo estudio estadístico, el investigador se interesa en una población que es el
conjunto de todas las observaciones de interés. Por ejemplo, el Ministerio de
Hacienda, está interesado en conocer los salarios de los trabajadores de España, ya
que según su cuantía así será la recaudación que esperará obtener en el próximo
ejercicio.
En estadística definimos variable como la característica de la muestra o población que
se quiere observar. Se clasifican de distintas maneras así distinguimos entre variables
cuantitativas y cualitativas; continuas y discretas…
Una serie temporal es un conjunto de datos ordenados en el tiempo, tomados a
intervalos regulares, procedentes normalmente de una magnitud económica de
definición constante a lo largo del tiempo.
Los parámetros son cualquier medida descriptiva de una población. Se entiende por
medida cualquier magnitud que simplifica o resume en un dato la información
contenida en toda la población. Así por ejemplo, el salario de todos y cada uno de los
trabajadores de España puede ser descrito de manera resumida por el salario medio
de esa misma población.
La muestra es una parte representativa de la población. Existen métodos para buscar
muestras representativas, dado que cualquier subconjunto de una población siendo
una muestra, no tiene porque representar las virtudes o defectos de la población, si la
muestra no se ha obtenido mediante procedimientos adecuados.
Estadístico es la medida que describe una muestra. Es una estimación del parámetro
de la población.
La muestra es importante ya que las poblaciones pueden ser muy grandes y recoger
información de estas es muy costoso. Asimismo, las muestras se recogen
rápidamente. Por estas razones, trabajar con estadísticos es conveniente.
No obstante, presenta algunas dificultades:
a) Errores en el muestreo: diferencia entre el parámetro desconocido de la
población y el estadístico de la muestra utilizada.
b) Sesgo muestral: es la tendencia a favorecer la elección de ciertos
elementos de la muestra en lugar de otros posibles.
La estadística tiene dos grandes ramas, una se dedica a describir la información
cuantitativa o cualitativa recogida que se pretende analizar. Recibe el nombre de
estadística descriptiva, es la que recoge, agrupa, resume y presenta los datos
obtenidos.
La otra rama de la estadística persigue anticipar resultados y analizando la información
pretende descubrir informaciones que permiten conocer lo que ocurrirá. Recibe el
nombre de estadística inferencial, persigue como su nombre indica, inferir o concluir
datos sobre la población a partir de los datos de la muestra.
44
fikai AULA FINANCIERA
5.1.2 MEDIA MUESTRAL Y ESPERANZA MATEMÁTICA
La media muestral se obtiene, a partir de un conjunto de datos muestrales
x 1, x 2 ,..., x n , al sumar el conjunto de valores de la variable y dividirlo por el numero de
observaciones:
x=
x1 + L + x n
n
Por otra parte, si los valores que puede tomar X están sometidos a incertidumbre,
estaremos ante una variable aleatoria que puede tomar los valores x 1, x 2 ,..., x n , con
probabilidades respectivas P( x 1 ),P( x 2 ),..., P( x n ) .
Se define la esperanza matemática o valor esperado de X como:
E( X) = x1·P(x1) + x 2 ·P(x 2 ) +L+ xn ·P(xn )
►EJEMPLO RESUELTO
Media y Esperanza
Las cotizaciones de las acciones BBVA en la última semana han sido: 16,01€; 16,35€;
16,22€; 16,21€; 15,94€. Calcular su media aritmética.
x=
16,01 + 16,35 + 16,22 + 16,21 + 15,94
= 16,14€
5
Supongamos ahora que un asesor se plantea determinar la cotización de las acciones
BBVA dentro de un mes, y prevé tres posibles escenarios:
Escenario
Cotización
Probabilidad
Pesimista
15 €
0,20
Normal
16,50 €
0,20
Optimista
17,20 €
0,60
Calcular la cotización esperada (esperanza matemática de la cotización).
E( X) = 15 x0,20 + 16,50 x0,20 + 17,20 x0,60 = 16,62€
fikai AULA FINANCIERA
45
5.2 Varianza y Desviación Típica
Capítulo 5: Conceptos estadísticos
A continuación introducimos medidas estadísticas que nos permitan representar la
dispersión respecto a la media de un conjunto de datos.
De nuevo distinguimos dos casos: Si hacemos referencia a valores pasados (datos
conocidos) o si hacemos referencia a valores futuros (incertidumbre en los datos).
A partir de un conjunto de datos muestrales x 1, x 2 ,..., x n , se define la varianza
muestral como el promedio de las desviaciones respecto a su media, elevadas al
cuadrado:
( x1 - x)2 + ( x 2 - x)2 + L + ( x n - x)2
S =
n
2
y la desviación típica muestral como la raíz cuadrada de la varianza muestral.
Se define es coeficiente de variación muestral como el cociente de la desviación
típica muestral y la media muestral.
g0 =
S
x
Por otra parte, si los valores que puede tomar X son x 1, x 2 ,..., x n , con probabilidades
respectivas P( x 1 ),P( x 2 ),..., P( x n ) . Se define la varianza poblacional de X como:
σ 2 = ( x 1 - E( X)) 2 ·P( x 1 ) + ( x 2 - E( X)) 2 ·P( x 2 ) + L + ( x n - E( X)) 2 ·P( x n )
y la desviación típica poblacional como la raíz cuadrada de la varianza poblacional.
La desviación típica muestral nos indica la dispersión de una variable respecto a su
valor promedio (si disponemos de datos históricos), mientras que la desviación típica
poblacional nos indica la fluctuación de una variable respecto a su valor esperado (en
el caso de valoración de activos es una medida del riesgo).
Se define es coeficiente de variación poblacional como el cociente de la desviación
típica poblacional y la media poblacional.
γ0 =
σ
E( X)
El coeficiente de variación mide la representatividad de la media (cuanto menor sea el
coeficiente, más representativa es la media), y nos permite comparar la
representatividad de los valores de distribuciones distintas.
46
fikai AULA FINANCIERA
►EJEMPLO RESUELTO
Varianza y Desviación Tipica
Las cotizaciones de las acciones BBVA en las cinco últimas sesiones han sido:
16,01€; 16,35€; 16,22€; 16,21€; 15,94€. La media aritmética es 16,146€.
Calcular la varianza y la desviación típica.
Cotización ( x i )
(x i - x)
( x i - x )2
16,01
- 0,136
0,018496
16,35
0,204
0,041616
16,22
0,074
0,005476
16,21
0,064
0,004096
15,94
- 0,206
0,042436
Σ=0
Σ = 0,11212
S2 =
0,11212
= 0,022424
5
y S = 0,022424 = 0,15€
EJMPLO RE
►EJEMPLO RESUELTO
Varianza y Desviación Típica
Si un asesor prevé los tres escenarios siguientes para la cotización de BBVA dentro de
un mes:
Escenario
Cotización
Probabilidad
Pesimista
15 €
0,20
Normal
16,50 €
0,20
Optimista
17,20 €
0,60
Su cotización esperada es E( X) = 16,62€ . Calcular la varianza y la desviación típica.
Escenario
Cotización
Probabilidad
( x i - E( X))
( x i - E( X))2
p i (·x i - E( X)) 2
Pesimista
15
0,20
- 1,62
2,6244
0,52488
Normal
16,50
0,20
- 0,12
0,0144
0,00288
Optimista
17,20
0,60
0,58
0,3364
0,20184
0,7296
La varianza será: σ 2 = 0,7296 y la desviación típica σ = 0,7296 = 0,85€
fikai AULA FINANCIERA
47
5.3 Covarianza y Correlación
Capítulo 5: Conceptos estadísticos
Hasta este momento hemos definido estadísticos referidos a una única característica
estadística. Para estudiar la existencia de relación entre dos variables (p.e. entre un
índice bursátil y la cotización de un título), necesitamos definir estadísticos que
relacionen dos conjuntos de datos.
Dados dos conjuntos de datos asociados de la siguiente manera:
X
Y
x1
y1
x2
y2
x3
y3
···
···
···
···
xn
yn
Se define la covarianza entre X e Y como:
S XY =
( x1 - x)·(y1 - y) + (x 2 - x)·(y 2 - y) + L+ ( xn - x)·(yn - y)
n
La covarianza indica la relación entre la variación de ambas variables y su
interpretación es la siguiente:
> Si S XY > 0 , la relación entre ambas variables es directa, es decir, se mueven en el
mismo sentido.
> Si S XY < 0 , la relación entre ambas variables es inversa, es decir, se mueven en
sentido contrario.
> Si S XY = 0 , no hay relación entre las variaciones de ambas variables.
La covarianza entre dos variables se ve afectada por las unidades de medida en las
que se expresen las variables, lo que hace necesario introducir un estadístico que nos
indique la relación entre los datos, sin depender de las unidades en las que se
expresen.
Se define el coeficiente de correlación lineal entre X e Y como:
rXY =
S XY
S X ·S Y
Mide también la relación lineal entre las variables, pero no depende de las unidades de
medida y está siempre comprendido entre –1 y 1.
48
fikai AULA FINANCIERA
INTERPRETACIÓN DEL COEFICIENTE DE CORRELACIÓN LINEAL
Y
> Si rXY ≈ 1 ⇒ relación lineal directa y fuerte
Si aumenta el valor de X, aumenta el valor de Y
X
Y
> Si rXY ≈ -1 ⇒ relación lineal inversa y fuerte
Si aumenta el valor de X, disminuye el valor de Y
X
Y
> Si rXY ≈ 0 ⇒ no se aprecia relación lineal
No se observa relación entre los valores de X e Y.
X
fikai AULA FINANCIERA
49
►EJEMPLO RESUELTO
Covarianza y Coeficiente de Correlación
Si las cotizaciones al cierre del Ibex-35 y de BBVA durante la segunda semana de
septiembre de 2007 han sido:
Ibex35 (X)
BBVA (Y)
10/09/07
13726,30
16,01
11/09/07
13965,50
16,35
12/09/07
13980,40
16,22
13/09/07
14077,80
16,21
14/09/07
13861,00
15,94
Sabiendo que la media del Ibex-35 de esa semana es de 13922,20 y la desviación de
119,6626 , y que la cotización media de BBVA es de 16,146 con una desviación de
0,1497, calcular la covarianza y el coeficiente de correlación lineal.
xi
yi
(x i - x)
(y i - y)
(x i - x) · (y i - y)
13726,30
16,01
-195,9
-0,136
26,6424
13965,50
16,35
43,3
0,204
8,8332
13980,40
16,22
58,2
0,074
4,3068
14077,80
16,21
155,6
0,064
9,9584
13861,00
15,94
-61,2
Σ=0
-0,206
12,6072
Σ=0
Σ = 62,348
S XY =
62,348
= 12,4696
5
y
r XY =
S XY
12,4696
=
= 0,6961
S X ·S Y 119,6626 · 0,1497
Interpretación: r XY = 0,6961, lo que indica que existe relación directa y no muy fuerte
entre la cotización del Ibex-35 y la cotización de BBVA.
►EJEMPLO PROPUESTO
Covarianza y Coeficiente de Correlación
Si las cotizaciones al cierre del Ibex-35 y de Telefónica durante la segunda semana de
septiembre de 2007 han sido:
Ibex35 (X)
TEF (Y)
10/09/07
13726,30
17,79
11/09/07
13965,50
18,18
12/09/07
13980,40
18,62
13/09/07
14077,80
19,10
14/09/07
13861,00
18,76
Calcular la covarianza y el coeficiente de correlación lineal entre las cotizaciones del
Ibex35 y Telefónica.
50
fikai AULA FINANCIERA
5.4 Regresión Lineal Mínimo Cuadrática
Capítulo 5: Conceptos estadísticos
La regresión lineal mínimo cuadrática nos proporciona una recta que se aproxima en la
mayor medida posible a la nube de puntos que resulta al representar los valores de
dos series de datos X e Y. El criterio más extendido para el cálculo de esta recta es el
Criterio Mínimo Cuadrático, que consiste en minimizar la suma de las desviaciones al
cuadrado entre los puntos y la recta.
Ecuación de la recta de regresión ŷ( x ) (para estimar los valores de Y a partir de los
valores de X)
ŷ = a + b·x , donde a = y - b·x y b =
S XY
S 2X
Para analizar la fiabilidad de esta estimación, se utiliza el coeficiente de determinación
dado por
2
R 2 = rXY
=
S 2XY
S 2X ·S 2Y
Sus valores cumplen que 0 ≤R 2 ≤1 y representa la proporción de información de la
serie que queda recogida en la recta de regresión (bondad del ajuste).
►EJEMPLO RESUELTO
Regresión lineal mínimo cuadrática
A partir de los datos del ejemplo resuelto anterior sobre la cotización del Ibex-35 y los
títulos de BBVA, hallar la recta de regresión que permita estimar la cotización de un
título de BBVA cuando el Ibex-35 alcance los 14200 puntos.
La recta de regresión lineal es ŷ = a + b·x , donde
b=
S XY
S 2X
=
12,4696
119,6626 2
= 0,00087
a = y - b·x = 16,146 - 0,00087 · 13922,20 = 4,034
luego: ŷ = a + b·x = 4,034 + 0,00087·x
Para estimar la cotización de BBVA para un Ibex-35 de 14200, sustituimos en la recta
de regresión x = 14200 y obtenemos:
ŷ(14200 ) = 4,034 + 0,00087 · 14200 = 16,39€
Si queremos analizar la fiabilidad de esta estimación, calculamos el coeficiente de
2
= 0,69612 = 0,4845 que nos indica que el 48,45% de la
determinación R 2 = r XY
información queda reflejada en esta recta y por tanto, la predicción no es muy fiable.
fikai AULA FINANCIERA
51
5.4.1 LINEA CARACTERÍSTICA DE UN TÍTULO (LCT)
Un ejemplo práctico de regresión lineal mínimo cuadrática lo constituye la Línea
Característica de un Título (LCT) o también llamado Modelo de Mercado de Sharpe.
Se toma como variable explicada la rentabilidad de un título “Rit“ y como variable
explicativa la rentabilidad de la cartera de mercado “RMt”, realizando la siguiente
regresión lineal:
R it = αi + β iR Mt + uit
donde Rit y RMt son, respectivamente, las rentabilidades del título i y de la cartera de
mercado en el momento t ; αi y βi son la ordenada en el origen y la pendiente del
ajuste ; y uit es la perturbación aleatoria correspondiente al título i en el momento t.
Gráficamente:
Línea Característica
del Título i
Rit
R it = αi + βiRMt + uit
αi
pendiente=βi
RMt
La pendiente de la recta LCT representada es lo que se conoce habitualmente como el
coeficiente beta del título, que es una medida de la relación entre la evolución de
la rentabilidad del título y la del mercado.
Las expresiones de βi y de αi obtenidas a través de la regresión lineal son:
βi =
siendo
cov(R i , RM ) σ iM
= 2
σ M2
σM
αi = Ei - βi • EM
σ iM =covarianza entre la rentabilidad del título (Ri) y la del mercado (RM)
σ M2 = varianza de la rentabilidad del mercado
Ei = rentabilidad esperada del título
EM = rentabilidad esperada del mercado
52
fikai AULA FINANCIERA
Distinguimos así entre distintos tipos de valores en función de su beta:
▪Títulos agresivos (β< -1 o β>1). Títulos más arriesgados que el índice
representativo del mercado, ya que una variación de un punto en el índice
provocará una variación mayor en la rentabilidad del título. Son títulos muy
sensibles a las oscilaciones del mercado.
▪Títulos defensivos (-1<β<1). Títulos menos arriesgados que el índice
representativo del mercado, ya que una variación de un punto en el índice
provocará una variación menor en la rentabilidad del título. Son títulos poco
sensibles a las oscilaciones del mercado.
▪Títulos neutros (β=-1 o β=1). Títulos que varían igual que el mercado.
De especial interés, si es que existen, son los títulos con beta negativa
(superdefensivos), ya que permitirían reducir el riesgo no diversificable.
Su precio habrá de ser forzosamente elevado, con lo que su rentabilidad será
reducida. Y por las condiciones del modelo, deberán ser (caso de existir), muy pocos,
ya que, lógicamente, la beta de la cartera de mercado (media ponderada de las betas
de los títulos que cotizan en el mercado) debe ser la unidad.
El coeficiente beta opera sobre el rendimiento de los títulos a modo de mecanismo que
filtra, amplifica o transmite sin interferencias las fluctuaciones del mercado, según se
trate de activos “defensivos”, “agresivos” o “neutros”.
►EJEMPLO RESUELTO
Línea Característica de un Título
La rentabilidad media del título A es del 12% y la rentabilidad media de mercado es del
8%. Sabiendo que la varianza de la rentabilidad de mercado es 0,18 y la covarianza
entre las rentabilidades del título A y del mercado es 0,23, obtener la Línea
Característica del Título.
La Línea Característica del título A viene determinada por la expresión:
R At = α A + β A R Mt + u At
donde:
El coeficiente beta del título A respecto al mercado: β A =
σ AM
2
σM
=
0,23
= 1,28
0,18
Estamos ante un título agresivo al ser β >1.
El coeficiente alfa del título A: α A = E A - β A ·E M = 0,12 - 1,28 x0,08 = 0,0176
En consecuencia la LCT sería: R At = 0,0176 + 1,28·R Mt + u At
fikai AULA FINANCIERA
53
RESUMEN DE CONCEPTOS
> Media aritmética: Valor promedio de una serie de datos históricos.
> Media poblacional o esperanza: Valor esperado de una variable cuando sólo
conocemos sus posibles valores y sus probabilidades.
> Desviación típica muestral: Desviación respecto a la media de una serie de datos
históricos.
> Desviación típica poblacional: Desviación respecto a la media de una variable
cuando sólo conocemos sus posibles valores y sus probabilidades. RIESGO.
> Covarianza: Mide la relación entre la variación de dos series de datos. Depende de
las unidades de medida.
> Coeficiente de correlación: Mide el grado de relación lineal entre dos series de
datos. Siempre está comprendido entre –1 y 1.
> Recta de regresión lineal: Recta obtenida a partir de dos series de datos, que nos
permite estimar los valores de una de las variables a partir de los valores de la otra.
> Coeficiente de determinación: Proporción de información de dos series de datos
que queda reflejada en la recta de regresión.
54
fikai AULA FINANCIERA
RESUMEN DE FÓRMULAS
ESTADÍSTICO
DATOS
Media
aritmética
x 1, x 2 ,..., x n
Esperanza
x 1, x 2 ,..., x n
P( x 1 ),P( x 2 ),...,P( x n )
Desviación
muestral
x 1, x 2 ,..., x n
Desviación
poblacional
FÓRMULA
x=
x1 + L + x n
n
E( X) = x 1·P( x 1 ) + L + x n ·P( x n )
( x 1 - x )2 + L + ( x n - x )2
S=
n
x 1, x 2 ,..., x n
σ = ( x 1 - E( X)) 2 ·P( x 1 ) + L + ( x n - E( X)) 2 ·P( x n )
P( x 1 ),P( x 2 ),..., P( x n )
Covarianza
x 1, x 2 ,..., x n
y 1, y 2 ,..., y n
Coef de
correlación
x 1, x 2 ,..., x n
y 1, y 2 ,..., y n
Recta de
regresión
x 1, x 2 ,..., x n
y 1, y 2 ,..., y n
Coef de
determinación
x 1, x 2 ,..., x n
y 1, y 2 ,..., y n
fikai AULA FINANCIERA
S XY =
(x1 - x)·(y1 - y) + L+ ( xn - x)·(yn - y)
n
rXY =
ŷ = a + b·x donde:
R
2
2
= rXY
S XY
S X ·S Y
a = y - b·x
=
b=
S XY
S 2X
S 2XY
S 2X ·S 2Y
55
►CUESTIONARIO
Capítulo 5: CONCEPTOS ESTADÍSTICOS
1. Las muestras son importantes porque
A) En ocasiones las poblaciones son grandes, o muy grandes.
B) Recoger información en las poblaciones es costoso.
C) Recoger información de las poblaciones requiere mucho tiempo.
D) Todas son ciertas.
2. La media aritmética es
A)
B)
C)
D)
Una medida alrededor de la cual se sitúan los datos.
Una medida de tendencia central.
Gráficamente el punto de apoyo de la distribución.
Cualquiera de las anteriores.
3. La desviación típica
A)
B)
C)
D)
Es la media de las desviaciones al cuadrado de los valores respecto a la media.
Es la raíz cuadrada de la varianza.
Es la diferencia entre el valor más alto y más bajo.
Todas son ciertas.
4. Si el coeficiente de regresión entre X = cotización del Ibex 35 e Y = cotización de AAA
es de 1,20:
A)
B)
C)
D)
Por cada punto que aumente el Ibex, la cotización de AAA disminuye 1,20 puntos.
La correlación entre X e Y es muy fuerte.
Por cada punto que aumente el Ibex, la cotización de AAA aumenta 1,20 puntos.
No existe relación entre el Ibex y AAA.
5. Un concesionario automovilístico ha vendido 14, 10, 13 y 19 automóviles en los cuatro
últimos trimestres. La desviación típica de ventas trimestral es
A)
B)
C)
D)
5 unidades.
3,24 unidades.
14 unidades.
4 unidades.
6. La desviación típica es un dato clave para medir la volatilidad o riesgo en el
comportamiento de una variable. ¿Cual de las siguientes fórmulas corresponde a la
desviación típica?
A) Raíz cuadrada del sumatorio de las distancias de cada dato con respecto a la media,
elevadas al cuadrado y divididas por el número de datos.
B) Raíz cuadrada del sumatorio de las diferencias de cada dato con respecto a la media,
elevadas al cuadrado y divididas por el número de datos.
C) Raíz cuadrada de la varianza.
D) Todas son ciertas.
7. Las cotizaciones de ABC en los cuatro últimos días han sido: 35’10€ 36€ 37’10€ y
37’90€. La desviación típica de estos precios es:
A)
B)
C)
D)
36’525.
1’13.
1’063.
Ninguna es cierta.
56
fikai AULA FINANCIERA
8. Para comparar distribuciones distintas es posible realizarlo con
A)
B)
C)
D)
Las medidas de tendencia central.
Con las medidas de dispersión habituales.
Con el coeficiente de variación.
Todas son ciertas.
9. El coeficiente de correlación está entre –1 y +1, el valor r = –1 indica
A)
B)
C)
D)
Relación positiva perfecta.
Relación negativa perfecta.
Que no existe relación.
Ninguna es cierta.
10. La teoría keynesiana del consumo establece que el consumo de las familias es
variable dependiente de los niveles de renta de las mismas. Queremos contrastar esta
afirmación y para ello estimamos una recta de regresión. Cual de las siguientes
afirmaciones es cierta
A) Podemos ver que la capacidad explicativa de la renta sobre el consumo es alta por el
coeficiente de regresión.
B) El porcentaje de variabilidad del consumo explicado por cambios en la renta vendrá medido
por el coeficiente de determinación, que toma valores entre –1 y 1.
C) El porcentaje de variabilidad del consumo explicado por cambios en la renta viene explicado
por el coeficiente de correlación que toma valores entre 0 y 1.
D) Ninguna es correcta.
11. Mi cartera tiene un coeficiente de regresión, o también llamado coeficiente beta de
sharpe, de 0,5, lo cual se interpreta como
A)
B)
C)
D)
Mi cartera explica el 50% de la variabilidad del mercado.
Mi cartera es agresiva.
Mi cartera ofrece rentabilidades por encima del mercado.
Ninguna es correcta.
12. Si el coeficiente de regresión vale 2,34, el coeficiente de correlación puede valer
A)
B)
C)
D)
-2,34
1,34
0,72
-0,72
13. El coeficiente de correlación lineal entre dos variables es r = 0,9. ¿Qué afirmación es
falsa?
A) La bondad del ajuste es del 81%. El modelo de regresión lineal explica el 81% de la
información contenida en los datos observados.
B) Ambas variables presentan una relación positiva .
C) Un incremento de la variable independiente se traslada a la variable dependiente con un
factor 0,9.
D) El coeficiente de correlación lineal es una medida adimensional comprendida entre -1 y 1,
independiente de los cambios de escala en las variables.
14. Hemos estimado un modelo de regresión lineal y = 1661+0,792x entre los gastos de
consumo y los ingresos anuales de las familias en una zona determinada. Para unos
ingresos anuales de 30.000€ el gasto de consumo estimado es
A)
B)
C)
D)
23.760 €
35.781 €
25.421 €
34.120 €
fikai AULA FINANCIERA
57
15. Tenemos la siguiente recta de regresión Y = a + b X . Las perturbaciones de la recta
de regresión, o errores entre el valor estimado y el calculado deben de cumplir las
siguientes condiciones
A) Los residuos deben tener media cero, varianza constante (homocedásticos) y dependencia
entre ellos.
B) Los residuos deben tener media uno, varianza constante (homocedásticos) y dependencia
entre ellos.
C) Los residuos deben tener media cero, varianza constante (homocedásticos) e
independencia entre ellos
D) Los residuos deben tener media uno, varianza constante (homocedásticos) e independencia
entre ellos.
16. Dos acciones A y B presentan el siguiente comportamiento: el día que A sube un
tanto por cien, B baja pero la mitad exacta en porcentaje; el día que A baja un tanto por
cien, B sube pero igualmente la mitad exacta en porcentaje. ¿Qué podemos decir sobre
el coeficiente de correlación r entre ambas variables y sobre la pendiente de la regresión
siendo p el porcentaje de variación diario.
A)
B)
C)
D)
r =1 , b= 0,5
r =1 , b= -0,5
r =-1 , b= -0,5
r =-1 , b= 0,5
17. Al estudiar el grado de asociación entre dos variables
A)
B)
C)
D)
Calculamos el coeficiente de correlación.
Calculamos el coeficiente de regresión.
Calculamos el coeficiente de determinación.
Todas son ciertas.
18. Queremos analizar como variaría el volumen de inversión en activos financieros que
disponen nuestros clientes ante cambios en sus niveles de renta. Para ello planteamos
A) Calcular el coeficiente de regresión en una relación lineal entre renta y volumen
inversión, siendo la renta la variable dependiente.
B) Calcular el coeficiente de regresión en una relación lineal entre renta y volumen
inversión, siendo la renta la variable independiente.
C) Calcular el coeficiente de determinación en una relación lineal entre renta y volumen
inversión.
D) Calcular el coeficiente de correlación en una relación lineal entre renta y volumen
inversión.
de
de
de
de
19. Mi cartera tiene un coeficiente de regresión o también llamado beta de Sharpe de 0,5,
lo cual se interpreta como
A)
B)
C)
D)
Mi cartera explica el 50% de la variabilidad del mercado.
Mi cartera sobre-reacciona ante cambios en las rentabilidades del mercado.
Mi cartera ofrece rentabilidades por encima del mercado.
Mi cartera es defensiva.
20. Se habla de regresión múltiple cuando
A)
B)
C)
D)
La variable y es función de una variable explicativa.
La variable y es función de dos o más variables explicativas.
La variable y es función de dos o más variables dependientes.
Todas son ciertas.
58
fikai AULA FINANCIERA
21. Un coeficiente de correlación próximo a -1 indica:
A)
B)
C)
D)
Relación directa y fuerte entre las variables.
Relación directa y débil entre las variables.
La recta de regresión proporciona un buen ajuste.
Al aumentar una de las variables, la otra variable disminuye en una unidad.
22. Las rentabilidades anuales observadas en los últimos años para un Fondo de
Inversión han sido: 20%, 10%, 0% y -10%. La desviación típica vale:
A)
B)
C)
D)
0%
11,18%
20%
Ninguna de las anteriores es correcta.
23. El coeficiente de correlación asume, por definición, valores comprendidos entre:
A)
B)
C)
D)
–2 y +2.
0 y +1.
–1 y + 1, ambos inclusive.
–1 y +1 , ambos exclusive.
24. ¿Cuál de las siguientes afirmaciones sobre la desviación estándar es incorrecta?
A)
B)
C)
D)
Es la raíz cuadrada de la covarianza.
Puede ser positiva o negativa.
Es la media aritmética de las observaciones por raíz de 252 días.
Todas las anteriores.
25. Un conjunto de datos ordenados en el tiempo, procedentes normalmente de
observaciones tomadas a intervalos regulares, como sucesión de valores que toma una
magnitud económica de definición constante a lo largo del tiempo, se denomina:
A)
B)
C)
D)
Intervalo de valores.
Variable aleatoria.
Variable estadística.
Serie temporal.
26. ¿Cuál de las siguientes afirmaciones sobre el coeficiente de determinación es
incorrecta?
A)
B)
C)
D)
Es el cuadrado del coeficiente de correlación.
Puede ser positivo o negativo.
Representa la proporción de información reflejada en la recta de regresión.
Toma valores entre 0 y 1.
27. ¿Cuál de las siguientes afirmaciones sobre la desviación estándar es correcta?
A)
B)
C)
D)
Toma valores positivos.
Puede ser positiva o negativa.
Es la raíz cuadrada de la covarianza.
Es la suma de las distancias al cuadrado de los datos a su media.
fikai AULA FINANCIERA
59
MÓDULO 1: FUNDAMENTOS DE LA INVERSIÓN
Capítulo 6. Rentabilidad y Riesgo
6.1 Rentabilidad
6.1.1 Rentabilidad histórica de un activo
6.1.2 Rentabilidad esperada de un activo
6.1.3 Rentabilidad histórica y esperada de una cartera
6.2 Riesgo
6.2.1 Volatilidad de un activo
6.2.2 Riesgo de una cartera de valores
6.3 Supuestos de la hipótesis de normalidad
fikai AULA FINANCIERA
61
6.1 Rentabilidad
Capítulo 6: Rentabilidad y Riesgo
En el ámbito de las inversiones (sean éstas de índole financiera o económica) el
análisis de la rentabilidad de las mismas constituye un punto de especial atención.
La rentabilidad del accionista es la relación que se establece entre lo que se ha
invertido en una determinada acción y el rendimiento económico o resultado que
proporciona. El rendimiento que un accionista puede obtener de una acción se mide
computando los dividendos percibidos, las plusvalías o revalorizaciones en su
cotización, así como las ventajas que puedan obtenerse por el carácter preferente de
las ampliaciones de capital vía derechos de suscripción preferente.
Podrías considerar dos tipos de rentabilidades:
> Rentabilidad a priori o rentabilidad esperada: se trata de una variable aleatoria de
carácter subjetivo que depende de nuestras expectativas. Como variable aleatoria
podrá tomar distintos valores, con unas probabilidades determinadas. La esperanza
matemática de dicha variable aleatoria nos proporciona una medida de la rentabilidad,
y su varianza nos da una medida de la dispersión o riesgo del activo financiero
correspondiente.
> Rentabilidad a posteriori o rentabilidad al final del plazo. Es una magnitud conocida
con certeza ya que vendrá determinada por el precio al inicio del periodo, precio al
final del periodo y los ingresos percibidos en el periodo.
En general, dado un periodo T, se utiliza la rentabilidad simple como medida de la
rentabilidad, que estudiamos en el capítulo 4, y se calcula como:
RS T =
PT + D T - P0 PT + D T
=
P0
P0
1
PT : Precio del título al final del periodo T
D T : Suma aritmética de todos los ingresos percibidos durante el periodo T.
P0 : Precio del título al inicio del periodo.
A priori, tan sólo se conoce el precio P0, por lo que para calcular la rentabilidad
deberemos estimar el resto de elementos.
A posteriori, todos los elementos que intervienen en la expresión anterior serán
conocidos, pudiendo determinar la rentabilidad.
Como comentábamos en el capítulo 4, la rentabilidad simple considera que los
rendimientos, tales como dividendos, derechos de suscripción, se perciben al final del
periodo, o que se reinvierten a una tasa del 0% si se perciben antes.
62
fikai AULA FINANCIERA
6.1.1 RENTABILIDAD A POSTERIORI DE UN ACTIVO
La rentabilidad a posteriori es la rentabilidad histórica al final del plazo. Podemos
conocer su valor con certeza ya que se calcula con datos históricos de un determinado
periodo.
►EJEMPLO RESUELTO
Rentabilidad Histórica
Sean las cotizaciones de las acciones AAA, a 31 de diciembre de los años 2001 a
2006 y los dividendos correspondientes a esos periodos:
Cotización
Dividendos
2001
21,30
2002
22,70
1,30
2003
20,50
1,25
2004
23,60
1,35
2005
25,00
1,38
2006
26,10
1,40
Calcular: (a) La rentabilidad simple para los años considerados.
(b) La rentabilidad anual media aritmética.
(c) La rentabilidad anual media geométrica.
(a) Para calcular la rentabilidad simple utilizamos la expresión:
RS T =
PT + D T - P0
P0
Así pues, la rentabilidad simple para el año 2002 es:
RS 2002 =
22,70 + 1,30 - 21,30
= 0,1268 = 12,68 %
21,30
Para el resto de los años, obtenemos las rentabilidades simples anuales:
Rentabilidad
2002
12,68%
2003
- 4,19%
2004
21,71%
2005
11,78%
2006
10%
(b) La rentabilidad anual media aritmética para el periodo 2002/2006 ha sido:
RT =
12,68 - 4,19 + 21,71 + 11,78 + 10
= 10,40 %
5
(c) Por último, a rentabilidad anual media geométrica será:
TGR T = 5 (1 + 0,1268 )·(1 - 0,0419 )·(1 + 0,2171)·(1 + 0,1178 )·(1 + 0,10 ) - 1 = 0,10 = 10 %
fikai AULA FINANCIERA
63
6.1.2 RENTABILIDAD ESPERADA DE UN ACTIVO
La rentabilidad a priori es una variable aleatoria de carácter subjetivo que depende de
nuestras expectativas. Como variable aleatoria podrá tomar distintos valores, con unas
probabilidades determinadas en función de unos escenarios (optimista, normal,
pesimista,...), pudiendo incluso utilizar la media histórica como un dato de referencia a
tener en cuenta.
Una vez realizadas las consideraciones anteriores, se habrá construido una variable
aleatoria de la forma:
Escenario
1
2
·
n
Rentabilidad
R1
R2
·
Rn
Probabilidad
p1
p2
·
Pn
La esperanza matemática de dicha variable aleatoria nos proporciona una medida de
la rentabilidad esperada del activo financiero correspondiente:
j=n
E T = R1·p1 + R 2 ·p 2 + L + R n ·p n =
∑R ·p
j
j
j=1
►EJEMPLO RESUELTO
Rentabilidad Esperada
En la siguiente tabla se recoge las estimaciones de un gestor sobre rentabilidades
semestrales para un activo A, según diferentes escenarios. Calcular la rentabilidad
esperada semestral de dicho activo A.
Escenario
Pesimista
Normal
Optimista
Rentabilidad
-4%
3%
10%
Probabilidad
0,20
0,50
0,30
ET= -4%·0,20 + 3%·0,50 + 10%·0,30 = 3,7% semestral
Para expresar la rentabilidad en términos anuales aplicamos una regla proporcional,
suponiendo que la inversión se comporta de la misma forma a lo largo del año y que
los intereses obtenidos no se reinvierten.
La rentabilidad anualizada esperada, si dividimos el año en N periodos, será:
E1= N· EN
Para anualizar rentabilidades mensuales N=12, semanales N=52 o diarias N=250.
►EJEMPLO RESUELTO
Rentabilidad Anualizada
Anualizar la rentabilidad semestral del ejemplo anterior
> E2 = 3,7% semestral
64
E1 = 2·E2 = 7,4 % anual
fikai AULA FINANCIERA
6.1.3 RENTABILIDAD ESPERADA DE UNA CARTERA
La rentabilidad de una cartera será igual a la media ponderada de las rentabilidades
de los activos que la componen. Se ponderarán las rentabilidades por el peso
específico que cada activo tiene en la cartera.
Dada una cartera formada por n títulos, con rentabilidades esperadas E1, E2, ... En y
pesos específicos x1, x2, ..., xn respectivamente, la rentabilidad esperada de la
cartera, denotada Ep, :
n
E p = x 1·E1 + x 2 ·E 2 + L + x n ·E n =
∑X ·E
j
j
j=1
> x 1 , x 2 , ..., x n son las proporciones de los respectivos activos en la cartera,
por tanto se cumple que x 1 + x 2 +...+ xn = 1.
>Para formar una cartera con la máxima rentabilidad con unos activos determinados,
hay que invertir todo el capital en el título que ofrezca la mayor rentabilidad esperada.
►EJEMPLO RESUELTO
Rentabilidad Esperada de una Cartera
Sea una cartera compuesta por 20.000 € en acciones, 5.000 € en depósitos bancarios
y 15.000 € en bonos. Las rentabilidades esperadas son respectivamente 12%, 4% y
5%. Calcular la rentabilidad esperada de la citada cartera.
Activo (i)
Acciones
Depósitos
Bonos
TOTAL
Inversión
20.000 €
5.000 €
15.000 €
40.000 €
R. Esperada
12%
4%
5%
Peso(xi)
0,5
0,125
0,375
1
La rentabilidad esperada de la cartera será:
E p = x 1·E1 + x 2 ·E 2 + L + x n ·E n = 0,5·12 + 0,125·4 + 0,375·5 = 8,375 %
Es evidente que si disponemos de 40.000€ para formar una cartera con estos tres
activos, obtendremos el mayor rendimiento esperado si destinamos los 40.000€ a la
compra de acciones, pero esta elección tendría un mayor riesgo que el reparto
original.
fikai AULA FINANCIERA
65
6.2 Riesgo
Capítulo 6: Rentabilidad y Riesgo
Según la R.A.E., el término riesgo significa contingencia o proximidad de un daño. En
términos financieros, entenderemos el “daño” como la posibilidad de obtener una
rentabilidad negativa, o bien de ganar menos de lo esperado.
Incertidumbre sobre el futuro. Grado de incertidumbre que acompaña a un préstamo o
a una inversión. Posibilidad de que el rendimiento efectivo obtenido de una inversión
financiera sea menor que el rendimiento esperado. Convencionalmente, se suele
utilizar como medida del riesgo la variabilidad en la tasa de los rendimientos que se
obtienen de la inversión, medida por la desviación típica o el coeficiente de variación.
Por tanto, definiremos riesgo como la incertidumbre que acompaña a una inversión.
Es la posibilidad de que el rendimiento efectivo obtenido de una inversión financiera
sea menor que el rendimiento esperado.
Convencionalmente, se suele utilizar como medida del riesgo la variabilidad en la tasa
de los rendimientos que se obtienen de la inversión, medida por la desviación típica.
6.2.1 VOLATILIDAD DE UN ACTIVO
Se define la volatilidad de un activo como la desviación típica de su rentabilidad.
Se denota σT y mide el grado de dispersión de la rentabilidad respecto a la rentabilidad
esperada.
►EJEMPLO RESUELTO
Volatilidad de un Título
Con los mismos datos que en el ejemplo visto en el apartado 6.1.2., calcular la
volatilidad del activo A.
Escenario
Ri
pi
Ri-ET
(Ri-ET)2
pi·(Ri-ET)2
Pesimista
Normal
Optimista
-0,04
0,03
0,10
0,20
0,50
0,30
- 0,077
- 0,007
0,063
0,005929
0,000049
0,003969
0,0011858
0,0000245
0,0011907
Calculamos primero la varianza, haciendo la suma de la última columna y obtenemos
σ2= 0,002401
Extraemos la raíz cuadrada y obtenemos la volatilidad σ = 0,049 = 4,9 %.
De manera análoga a la rentabilidad anualizada, podemos plantearnos el cálculo de la
volatilidad anualizada de un título haciendo:
σ1= N ·σN
66
fikai AULA FINANCIERA
6.2.2 RIESGO DE UNA CARTERA DE VALORES
Para calcular la volatilidad de una cartera, no sólo debemos tener en cuenta las
volatilidades de cada uno de los títulos, sino que debemos considerar también el grado
de correlación que presentan entre sí los títulos que la componen.
Se define la volatilidad de una cartera como la desviación típica de la rentabilidad de
la cartera y se denota σP.
> Expresión de la volatilidad de una cartera formada por dos valores:
σ P = x 12 ·σ 12 + x 22 ·σ 22 + 2·x 1·x 2 ·σ 12
Como ρ12 =
σ 12
σ1·σ 2
σ12 = ρ12 ·σ1·σ 2 Sustituyendo en la volatilidad σP
σ P = x12 ·σ12 + x 22 ·σ 22 + 2·x1·x 2 ·ρ12 ·σ1·σ 2
CASOS PARTICULARES:
ƒ ρ12 = -1
σ P = x12 ·σ 12 + x 22 ·σ 22 - 2·x1·x 2 ·σ 1·σ 2 = ( x1·σ1 - x 2 ·σ 2 ) 2 = x1σ1 - x 2 σ 2
En este caso podemos construir una cartera de riesgo nulo σP = 0 :
x1 =
ƒ ρ12 = 0
σ2
σ1 + σ 2
y x2 =
σ1
σ1 + σ 2
σ P = x12 ·σ 12 + x 22 ·σ 22
En este caso la cartera de mínimo riesgo será la siguiente:
x1 =
ƒ ρ12 = 1
σ 22
σ12 + σ 22
y x2 =
σ12
σ12 + σ 22
σ P = x12 ·σ 12 + x 22 ·σ 22 + 2·x1·x 2 ·σ 1·σ 2 = ( x1·σ1 + x 2 ·σ 2 ) 2 = x1σ1 + x 2 σ 2
En este caso la cartera de mínimo riesgo estará formada en su totalidad por el título
de menor riesgo.
fikai AULA FINANCIERA
67
> Expresión de la volatilidad de una cartera formada por tres valores:
σ P = x 12 ·σ 12 + x 22 ·σ 22 + x 32 ·σ 32 + 2·x 1·x 2 ·σ 12 + 2·x 1·x 3 ·σ 13 + 2·x 2 ·x 3 ·σ 23
> Si la cartera está formada por más de tres títulos, la expresión se generaliza
análogamente.
Como puede observarse el riesgo de una cartera depende en gran medida de la
correlación entre los títulos que la componen.
►EJEMPLO RESUELTO
Volatilidad de una Cartera
Sea una cartera P formada por un 40% de acciones, un 30% de Bonos y un 30% de
Depósitos. La rentabilidad esperada, la volatilidad y la correlación entre las acciones,
bonos y depósitos vienen recogidas en la siguiente tabla.
Calcular la volatilidad de la cartera P.
Activo
Peso
R. Esperada
Riesgo
Acciones
Bonos
Depósitos
0,4
0,3
0,3
12%
5%
4%
20%
8%
3%
Correlaciones
Acciones
Bonos
Depósitos
1
0,35
0,07
0,35
1
0,2
0,07
0,2
1
Calculamos primero las covarianzas entre las rentabilidades de los diferentes valores,
según la expresión σij = ρij·σi·σj.
σ12 = 0,35·0,20·0,08 = 0,0056
σ13 = 0,07·0,20·0,03 = 0,00042
σ23 = 0,2·0,08·0,03 = 0,00048
Aplicar la fórmula de la volatilidad de una cartera de tres títulos, obteniendo:
0,42 ·0,22 + 0,32 ·0,082 + 0,3 2 ·0,032 + 2·0,4·0,3·0,0056 + 2·0,4·0,3·0,00042 + 2·0,3·0,3·0,00048
luego σP=
0,0085882 = 0,09267
►EJEMPLO RESUELTO
Rentabilidad esperada y volatilidad de una cartera
Un gestor construye una cartera P con dos títulos (1 y 2) que tienen un coeficiente de
correlación entre sus rentabilidades de 0,35. Las rentabilidades esperadas son del
20% y 10%, y las volatilidades del 28% y del 16% respectivamente.
Obtener la rentabilidad y la volatilidad de una cartera compuesta por un 30% de 1 y un
70% de 2.
EP = 0,30·0,20 + 0,70·0,10 = 0,13 = 13%
σP =
68
0,30 2 · 0,28 2 + 0,70 2 · 0,16 2 + 2 · 0,30 · 0,70 · 0,35 · 0,28 · 0,16 =16,18%
fikai AULA FINANCIERA
6.3 Supuestos de la hipótesis de normalidad
CapítuloE(x)+2σ
6: Rentabilidad y Riesgo
En la práctica, se acepta que una serie de datos referida a la rentabilidad de un activo
o una cartera sigue una Ley Normal, que se caracteriza por dos parámetros: la
rentabilidad esperada (esperanza matemática) y la volatilidad (desviación típica).
a = 2,5%
a + b = 16%
b
b
a
E(x)-2σ
a
E(x)-σ
E(x)
E(x)+σ
En el caso de que la rentabilidad de un activo o de una cartera se ajuste a una ley
normal de media E y desviación típica σ, podemos afirmar que:
> Hay aproximadamente una probabilidad del 68% de que la rentabilidad del activo
se encuentre entre E-σ y E+σ. El 32% restante se reparte entre la probabilidad de que
la rentabilidad sea mayor que E+σ (16%) y la probabilidad de que la rentabilidad sea
menor que E-σ (16%).
> Hay aproximadamente una probabilidad del 95% de que la rentabilidad del activo
se encuentre entre E-2σ y E+2σ. El 5% restante se reparte entre la probabilidad de
que la rentabilidad sea mayor que E+2σ (2,5%) y la probabilidad de que la rentabilidad
sea menor que E-2σ (2,5%).
> Hay aproximadamente una probabilidad del 99% de que la rentabilidad del activo
se encuentre entre E-3σ y E+3σ. El 1% restante se reparte entre la probabilidad de
que la rentabilidad sea mayor que E+3σ (0,5%) y la probabilidad de que la rentabilidad
sea menor que E-3σ (0,5%).
►EJEMPLO RESUELTO
Consecuencias de la Hipótesis de Normalidad
Una cartera tiene una rentabilidad esperada del 15% con una volatilidad del 10%.
Hallar intervalos alrededor de la rentabilidad media con probabilidades del 68% y del
95% respectivamente.
Si aceptamos que la rentabilidad sigue una ley Normal, podemos afirmar que:
> Existe una probabilidad del 68% de que la rentabilidad se encuentre entre
15 - 10 y 15 + 10. Por tanto, el intervalo (5% , 25%) concentra una probabilidad del
68%.
> Existe una probabilidad del 95% de que la rentabilidad se encuentre entre
15 - 2·10 y 15 + 2·10. Por tanto, el intervalo (-5% , 35%) concentra una probabilidad
del 95%.
fikai AULA FINANCIERA
69
►RESUMEN DE CONCEPTOS
> Rentabilidad Simple de una inversión: Variación porcentual que experimenta el
valor de un activo durante un periodo.
> Rentabilidad Histórica de un activo: Determinada por el precio al inicio del
periodo, precio al final del periodo y los ingresos percibidos en el periodo. Para
calcular la rentabilidad media de un periodo de varios años, se utiliza la media
geométrica de las rentabilidades anuales.
> Rentabilidad Esperada de un activo: Al inicio de la inversión, sólo se conoce el
valor de P0, por lo que habrá que hacer estimaciones sobre los otros valores para
estimar la rentabilidad. Es la esperanza matemática de la rentabilidad.
> Rentabilidad Esperada Anualizada de un activo: Es la rentabilidad anual que se
obtendría suponiendo que los intereses obtenidos no se reinvierten y que el
comportamiento de la inversión se va a repetir a lo largo del año.
> Rentabilidad Esperada de una cartera: Media ponderada de las rentabilidades
de cada uno de los títulos, ponderada por los pesos de los títulos en la composición de
la cartera.
> Riesgo: Incertidumbre que genera la fluctuación de la rentabilidad de un activo en
torno a su rentabilidad esperada
>
Volatilidad de un título: Medida del riesgo. Desviación típica de la rentabilidad.
> Volatilidad de una cartera: Medida del riesgo de una cartera. No coincide con la
media ponderada de las volatilidades de cada título.
> Consecuencias de la hipótesis de normalidad: Si la rentabilidad sigue una Ley
Normal, la probabilidad de que la rentabilidad de un activo se encuentre entre E - σ y E
+ σ es del 68% y la probabilidad de que la rentabilidad de un activo se encuentre entre
E - 2σ y E + 2σ es del 95%.
70
fikai AULA FINANCIERA
►RESUMEN DE FÓRMULAS
CONCEPTO
DATOS
FÓRMULA
Rentabilidad
Simple
PT=Precio final
DT=Dividendos
P0=Precio final
Rentabilidad
Geométrica
RS1,RS2, ..., RSN
TGR N = N (1+ RS1 )·L·(1+ RS N ) - 1
Rentabilidad
Esperada
R1, ..., Rn
p1, ..., pn
E T = R1·p1 + R 2 ·p 2 + L + R n ·p n = ΣRj·pj
Rentabilidad
Esperada
Anualizada
N = número de
períodos en los que
dividimos el año
E1= N· EN
Rentabilidad
esperada
de una cartera
x ,..., x proporciones
1
n
RS T =
PT + D T - P0
P0
E ,..., E rentabilidades
E p = x 1·E1 + x 2 ·E 2 + L + x n ·E n = Σxj·Ej
Volatilidad
de un título
R1, ..., Rn
p1, ..., pn
σ p = (R1 - E T ) 2 ·p1 + L + (R n - E T ) 2 ·p n
Volatilidad
Anualizada
N = número de
períodos en los que
dividimos el año
σ1= N ·σN
Volatilidad
de una cartera
(2 títulos)
1
n
x , x proporciones
1
2
σ , σ volatilidades
1
σ P = x 12 ·σ 12 + x 22 ·σ 22 + 2·x 1·x 2 ·σ 12
2
x , x , x proporciones
Volatilidad
de una cartera
(3 títulos)
Consecuencias
de Normalidad
1
2
3
σ , σ , σ volatilidades
1
σ
ij
2
3
σP = x12·σ12 +x22·σ22 +x32·σ32 +2·x1·x2·σ12+2·x1·x3·σ132·x2·x3·σ23
covarianzas
E, σ
fikai AULA FINANCIERA
P(E-σ , E+σ)= 0,68
P(E-2σ , E+2σ)= 0,95
P(E-3σ , E+3σ)= 0,99
71
►CUESTIONARIO
Capítulo 6: RENTABILIDAD Y RIESGO
1. Aunque en finanzas vinculamos el concepto de riesgo a un determinado estadístico,
¿cuál de las siguientes definiciones podría también aproximar el concepto de riesgo?
A) Posibilidad de obtener una rentabilidad negativa.
B) Existencia de una elevada fluctuación de la rentabilidad del activo respecto al valor de su
rentabilidad esperada.
C) Posibilidad de obtener una rentabilidad inferior a la que ofrece el activo libre de riesgo.
D) Todas podrían aproximarse al concepto de riesgo.
2. Con criterio de buen gestor elija entre las siguientes opciones
A)
B)
C)
D)
Una cartera formada por 20 títulos con rentabilidad media del 3% y volatilidad 2%.
Un activo con rentabilidad media del 3% y volatilidad 2%.
Una cartera formada por 10 títulos con rentabilidad media del 3% y volatilidad 2%.
Dependerá de las preferencias del usuario.
3. A la hora de calcular la rentabilidad de una cartera
A) No influirá el nivel de correlación entre los activos.
B) Se calcula como media ponderada de las rentabilidades de los activos, considerando la
ponderación como el peso del activo en la cartera.
C) Nunca podrá superar la rentabilidad del activo más rentable.
D) Todas son ciertas.
4. La cartera de un inversor esta constituida únicamente por 4 títulos. Sabiendo que en la
cartera todos los títulos tienen el mismo peso y que sus rentabilidades respectivas son
iguales a 3,2%, 3,6%, 4% y 2,4% ¿cuál es la tasa de rentabilidad global de la cartera?
A)
B)
C)
D)
3,3%
3,6%
2,4%
3,10%
5. Indique cuál es la rentabilidad total anualizada de un fondo que ha obtenido un 6% en
su primer año, y un 12,5% en su segundo año.
A)
B)
C)
D)
9,25%
18,50%
9,20%
9,50%
6. Un mercado de acciones presenta una desviación típica mensual con respecto a su
rentabilidad igual al 2%. ¿Cuál de los valores siguientes aproxima mejor la estimación de
la desviación típica anual de dicho mercado?
A)
B)
C)
D)
24%
21%
7%
10%
7. Cuando en finanzas hablamos de volatilidad o riesgo de un instrumento financiero, ¿a
qué operador estadístico nos estamos refiriendo?
A) Raíz de la varianza.
B) Desviación típica.
C) A la raíz del sumatorio de las desviaciones con respecto a la media al cuadrado, dividido
entre el número de datos
D) Todas son ciertas.
72
fikai AULA FINANCIERA
8. Esta mañana ha llegado a nuestra oficina un cliente y nos ha pedido que le
construyamos una cartera con dos instrumentos financieros, tratando únicamente de
maximizar su rentabilidad. Las rentabilidades medias son del 5% y del 7%, y
volatilidades del 2,5% y del 3% respectivamente. ¿Cuál sería la ponderación asignada a
cada uno de los instrumentos?
A) El óptimo estaría en un 50% de cada uno.
B) No hay una cartera óptima en este caso.
C) Crearía una cartera únicamente con el instrumento más rentable.
D) Tendría que tener en cuenta la correlación para maximizar la rentabilidad.
9. Rentabilidad y riesgo son dos conceptos estrechamente vinculados en la gestión de
toda cartera. ¿Cuál de las siguientes opciones sería la más deseable desde el punto de
vista de la racionalidad económica?
A)
B)
C)
D)
Cartera A: Rentabilidad muy alta / Volatilidad menor que cero.
Cartera B: Rentabilidad alta / Volatilidad menor que cero.
Cartera C: Rentabilidad cero / Volatilidad cero.
Cartera D: Rentabilidad alta / Volatilidad cero.
10. El objetivo de la diversificación dentro de una cartera será obtener
A)
B)
C)
D)
Aumentos de la rentabilidad.
Una rentabilidad media unido a un determinado riesgo medio.
Incrementos del número de títulos.
Reducción del riesgo.
11. Considera una cartera P de acciones A, B y C con las siguientes características:
Acción
A
B
C
Nº de Acciones
en la Cartera P
20
10
40
Precio por acción Rentabilidad
en €
Esperada
1000
10%
2000
2%
1500
18%
Varianza
Beta
0,01
0,04
0,09
0,6
-0,2
1,4
¿Cuál es la rentabilidad esperada de la cartera P?
A)
B)
C)
D)
13.20%
8.80%
10.00%
Ninguna de las respuestas anteriores.
12. Un título con una rentabilidad esperada del 10% y una volatilidad del 6% que siga una
Ley Normal tiene una probabilidad aproximada del 68% de que su rentabilidad oscile
entre:
A)
B)
C)
D)
Un 4% y un 16%
Un -8% y un 48%
Un -2% y un 22%
Un 0% y un 34%
13. Los activos A y B tienen una desviación estándar de 10% y 20% respectivamente. La
correlación entre el activo A y B es de -1. ¿Cuál será la desviación estándar de una
cartera compuesta por la mitad del activo A y por la mitad del activo B?
A)
B)
C)
D)
10%
15%
5%
30%
fikai AULA FINANCIERA
73
14. Cuál de las siguientes afirmaciones sobre la desviación estándar es correcta.
A)
B)
C)
D)
Es la raíz cuadrada de la varianza.
Puede ser positiva o negativa.
Es la media aritmética de las observaciones.
Ninguna de las anteriores es correcta.
15. Conocido un conjunto de datos distribuidos normalmente, de media 35000 y
desviación típica de 4540. ¿Qué porcentaje de observaciones están entre 35000-39540?
A)
B)
C)
D)
68%
9,05%
47,5%
Ninguna de las anteriores.
16. Un mercado de acciones presenta una desviación típica semanal con respecto a su
rentabilidad igual al 3 % ¿Cuál de los valores siguientes aproxima mejor la estimación de
la desviación típica anual de dicho mercado?
A)
B)
C)
D)
150 %
21 %
10 %
25 %
17. Conocido un conjunto de datos distribuidos normalmente de media 35000 y
desviación típica de 4540. ¿Qué porcentaje de observaciones están entre 35000-44080?
A)
B)
C)
D)
81,90%
9,05%
47,5%
Ninguna de las anteriores.
18. ¿Qué método es el más adecuado para medir la rentabilidad obtenida por un gestor
en el pasado?
A)
B)
C)
D)
Media aritmética.
Composición o media geométrica.
TIR.
Plusvalías latentes.
19. Dos acciones A y B presentan una desviación típica anual con respecto a su
rentabilidad igual, respectivamente, al 20% y al 12%, así como un coeficiente de
correlación entre rentabilidades igual a 0. ¿Cuál sería la desviación típica de una cartera
que contuviera ambos títulos igualmente ponderados?
A)
B)
C)
D)
14,22%
0%
11,66%
16%
20. Si las rentabilidades anuales de un fondo han sido: 40%, 10%, -2%
A)
B)
C)
D)
Su desviación típica es de 17,66.
Su desviación típica es de 3,9.
Su desviación típica es de 5,2.
Ninguna de las anteriores.
21. Entre dos activos cualesquiera, se considera más arriesgado:
A)
B)
C)
D)
El que tenga mayor volatilidad.
El que tenga menor liquidez.
El que tenga menor coeficiente de correlación.
El que tenga mayor rentabilidad esperada.
74
fikai AULA FINANCIERA
22. La volatilidad de un activo se mide mediante:
A)
B)
C)
D)
La varianza.
La desviación típica.
La covarianza.
El coeficiente de correlación.
23. Cuanto más bajo sea el coeficiente de correlación entre dos activos de una cartera:
A)
B)
C)
D)
Mayor será la varianza de la cartera.
Mayor será la rentabilidad de la cartera.
Menor será la varianza de la cartera.
No depende de la correlación.
24. Supongamos que la variable aleatoria "rendimiento esperado" de un activo financiero
sea continua y presente una distribución normal de frecuencias. Si la media de los
rendimientos referidos a un período temporal dado es el 9% y la desviación estándar es
el 3%, ¿cuál es la probabilidad de que el rendimiento del activo se sitúe entre el 3% y el
15%?
A)
B)
C)
D)
Cerca del 50%
Cerca del 68%
Cerca del 99%
Cerca del 95%
25. Una inversión por un valor de 6.534 € ha reportado unos dividendos semestrales de
243€, 240€ y 105€. Al año y medio se ha liquidado la inversión por un valor de 7.012€. La
rentabilidad simple obtenida ha sido:
A)
B)
C)
D)
7,31%
9%
16,31%
10,60%
fikai AULA FINANCIERA
75
►SOLUCIÓN DE LOS CUESTIONARIOS
Módulo 1: FUNDAMENTOS DE LA INVERSIÓN
CAPÍTULOS
1, 2 y 3
1
B
2
A
3
B
4
B
5
C
6
B
7
A
8
A
9
B
10
A
11
B
12
D
13
C
14
B
15
D
16
A
17
B
18
C
19
C
20
C
21
B
22
C
23
A
CAPÍTULO 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
D
B
C
D
C
B
C
D
D
C
B
C
C
D
D
A
CAPÍTULO 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
D
D
B
C
B
D
C
C
B
D
D
C
C
C
C
C
A
B
D
B
C
B
C
D
D
B
A
CAPÍTULO 6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
D
A
D
A
C
C
D
C
D
D
A
A
C
A
D
B
C
B
C
A
A
B
C
D
C
►BIBLIOGRAFÍA
Módulo 1: Fundamentos de la Inversión
▪ ALEGRE ESCOLANO, P. y otros (1990): "Ejercicios resueltos
Matemáticas de las Operaciones Financieras". Ed. AC, Madrid.
de
▪ BETZUEN ZALBIDEGOITIA, Amancio (2001): "Curso de Matemáticas
Financieras: Análisis Financiero Fundamental, Rentas y Constitución de
Capitales". Instituto de Estudios Financiero-Actuariales. Bilbao.
▪ BETZUEN ZALBIDEGOITIA, Amancio (1992): "Curso de Matemáticas
Financieras: Operaciones de Préstamos, Operaciones de Empréstito
obligaciones". Instituto de Estudios Financiero-Actuariales. Bilbao.
▪ BETZUEN, Amancio; BILBAO, Alberto; GOMEZ, Rosalía; DE LA PEÑA,
J.Iñaki(1994): "Matemática Financiera: Ejercicios resueltos". Instituto de
Estudios Financiero-Actuariales. Bilbao.
▪ DE PABLO LOPEZ, A. (1994): "Matemática de las operaciones Financieras".
Vol. 1 y 2. Ed. UNED. Madrid.
▪ GONZALEZ CATALA, V. (1991): "Enfoque práctico de las Operaciones de la
Matemática Financiera". Ed. Ciencias Sociales. Madrid.
▪ Bárcena, M.J.; Fernández, K.; Ferreira, E. y Garín, M.A. (2003). Elementos de
Probabilidad y Estadística Descriptiva. Servicio Editorial de la Universidad del
País Vasco, UPV/EHU.
▪ J. Arteche et al. (2000). Ejercicios de estadística I. Elementos de Probabilidad
y Estadística. Servicio Editorial de la UPV/EHU.
▪ Martín Pliego, F.J.; Ruiz Maya, L. (2004). Estadística I: Probabilidad, Editorial
AC, 2ª edición. Madrid.
▪ Martín Pliego, J.M. Montero Lorenzo y F.J.; Ruiz Maya (2002). Problemas de
Probabilidad, Editorial AC, Madrid.
▪ Tusell, F. y Garín, A. (1991). Ejercicios de Probabilidad e Inferencia
Estadística. TébarFlores, Madrid.
▪ Martín Pliego, F.J. (1994). Introducción a la Estadística Económica y
Empresarial. Editorial AC., Madrid.
▪ “Estadística aplicada a los negocios y la economía”. Allen L. Webster. Tercera
Edición. Mc Graw-Hill: Irwin- Mc Graw-Hill.2000
▪ “Probabilidad y Estadística. Aplicaciones y Métodos”. George C. Canavos.
Editorial Mc Graw Hill. 1997
▪ “Probabilidad y Estadística”. Ronald E. Walpole y Raymond H. Myers. Cuarta
Edición. Editorial Mc Graw Hill.
fikai AULA FINANCIERA