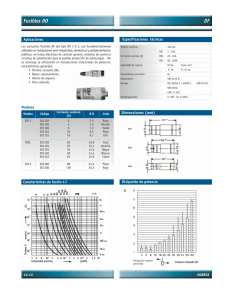
x )yx(m `Kqq dt dv + = y )yx(m `Kqq dt dv + =

Electricidad y Magnetismo
PRÁCTICA CASERA Nº 1
MODELAMIENTO DE LA TRAYECTORIA DE UNA PARTÍCULA CARGADA
EN PRESENCIA DE OTRA CARGA FIJA
Análisis Numérico
1.
OBJETIVOS
1.1. Afianzar la Ley de Coulomb.
1.1. Mostrar que la Ley de Coulomb permite determinar la trayectoria descrita por una
partícula cargada.
1.2. Verificar numéricamente que el campo electrostático es conservativo.
2. CONCEPTOS A AFIANZAR
2.1. Ley de Coulomb.
2.2.Energía Potencial Eléctrica.
2.3.Conceptos Previos:
2.3.1. Conceptos Cinemáticos: Posición, Velocidad y Aceleración.
2.3.2. Segunda ley de Newton.
2.3.3. Fuerzas Conservativas.
2.3.4. Energía Cinética.
2.3.5. Energía Mecánica.
3. TÉCNICAS EXPERIMENTALES
3.1.Simulación numérica por métodos iterativos.
4. TIEMPO NECESARIO PARA EL DESARROLLO
2 a 4 Horas.
5. MATERIAL REQUERIDO
5.1.Calculadora o Computadora.
5.2.Papel milimetrado.
6. RECOMENDACIONES
6.1.Haciendo uso de la ley de Coulomb vectorial en el plano XY y la segunda ley de
Newton, analice un sistema compuesto por dos cargas eléctricas (q y q’), una de ellas en
el origen (q’), y demuestre que para la carga q se tiene:
dv x
Kqq'

x
2
2 3/ 2
dt
mq (x  y )
dv y
dt

Kqq'
y
2
2 3/ 2
mq (x  y )
6.2.Teniendo en cuenta la definición de derivada y haciendo “caso omiso” del límite
involucrado en dicha definición podemos ver que para la coordenada X:
v x ( t  t )  v x ( t )  v x
donde
v x 
Kqq'
x t
2
2 3/ 2
mq (x  y )
X (t  t )  X (t )  X
X  v  t
donde
x
6.3.Obtenga las ecuaciones correspondientes para la coordenada Y.
6.4.Con ayuda de las ecuaciones anteriores construya una tabla como la tabla 1 (con màs de
100 filas), usando como valores iniciales las cantidades mostradas en los cuadros con
recuadro doble. Las columnas Ek, Ep y Et son las energías cinética, potencial eléctrica
y mecánica total del sistema respectivamente. Las características de las cargas
involucradas aparecen en la tabla 2 y corresponden a un átomo de hidrógeno (q’= +e ;
q = - e y m q = 9,1 x10-31 kg). Si le es posible realice la tabla en una hoja de Excel.
t(s)
X(m)
t0 = 0
-5.3000
E-11
X
Y(m)
Y
0.0000
E+00
Vx(m/s)
Vx
Vy(m/s)
0.0000
E+00
2.19
E+06
Vy
Ek
Ep
Et
2.18 -4.35 -2.17
E-18 E-18 E-18
t1 = t0+t
-5.300 0.00
E-11 E+00
6.998 7.00
E-13 E-13
2.884 2.88
E+04 E+04
2.19
E+06
0.000 2.18 -4.35 -2.17
E+00 E-18 E-18 E-18
t2 = t1+t
-5.297
E-11
2.099 7.00
E-12 E-13
8.650 2.88
E+04 E+04
2.19
E+06
-7.612 2.18 -4.35 -2.17
E+02 E-18 E-18 E-18
1.85
E-14
Tabla 1
m = 9.10E-31
q’ = 1.60E-19
q=
-1.60E-19
K = 9.00E+09
t = 3.20E-19
Tabla 2
6.5.En una hoja de papel milimetrado ubique las coordenadas X, Y de la tabla obtenida (por
facilidad no ubique la totalidad de las coordenadas, sino cada 5 o cada 10 valores de
X,Y).
6.6.Repita el proceso anterior para: q’= +79e ; q = +2e ; mq = 6,4x10-27 kg con valores
iniciales de X = 5x10 –14 m ; Y = 1x10-15 m. ; vx = -3,2x107 m/s; vy = 0,0 con t =
1x10-23 s.
7. TIPO DE INFORME REQUERIDO
Formato de artículo para revista. Máximo 5 páginas.
8. PREGUNTAS
8.1.Enumere al menos tres causas posibles de error.
8.2.¿Con qué porcentaje de error podemos asegurar que se cumple el principio de
conservación de la energía mecánica?
8.3.Estime la incertidumbre asociada al último valor de energía total obtenido en la tabla.
9. BIBLIOGRAFÍA
S. Lea and J. Burke, PHYSICS, The Nature of Things,
Brooks/Cole Publishing Company, 1997,
Secciones: 23.1.2; 25.1.1; 25.1.2; 25.1.3; 25.2.1.