Tablas (intervalos para poblaciones normales)

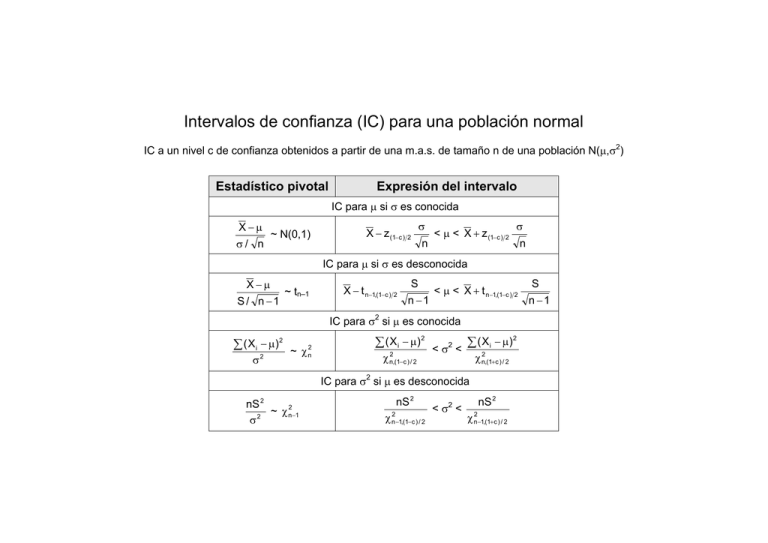
Intervalos de confianza (IC) para una población normal
IC a un nivel c de confianza obtenidos a partir de una m.a.s. de tamaño n de una población N(µ,σ2)
Estadístico pivotal
Expresión del intervalo
IC para µ si σ es conocida
X−µ
σ/ n
~ N(0,1)
X − z (1−c ) 2
σ
n
< µ < X + z (1−c ) 2
σ
n
IC para µ si σ es desconocida
X−µ
S / n −1
~ tn–1
X − t n−1,(1−c ) 2
S
n −1
< µ < X + t n−1,(1−c ) 2
IC para σ2 si µ es conocida
∑ ( X i − µ)2 ~ χ 2
n
2
σ
∑ ( X i − µ ) 2 < σ2 < ∑ ( X i − µ ) 2
2
2
χ n,(1−c ) / 2
χ n,(1+c ) / 2
IC para σ2 si µ es desconocida
nS 2
2
~ χ n−
1
2
σ
nS 2
χ n2−1,(1−c ) / 2
2
<σ <
nS 2
χ n2−1,(1+c ) / 2
S
n −1
Intervalos de confianza (IC) para comparar dos poblaciones normales
IC a un nivel c de confianza obtenidos a partir de dos mm.aa.ss. de tamaños respectivos n y m,
extraídas de sendas poblaciones N(µX,σ2X) y N(µY,σ2Y).
Estadístico pivotal
Expresión del intervalo
IC para µX–µY si σX y σY son conocidas
X − Y − (µ X − µ y )
σ
σ
+
n
m
2
X
2
Y
~ N(0,1)
X − Y − z (1−c ) 2
σ 2X σ 2Y
σ 2X σ 2Y
+
< µX–µY < X − Y + z (1−c ) 2
+
n
m
n
m
IC para µX–µY si σX y σY son desconocidas pero iguales
X − Y − (µ X − µ y )
nS + mS n + m
n + m − 2 nm
2
X
2
Y
~ tn+m-2
X − Y − t n+m−2,(1−c ) 2
nS 2X + mS 2Y n + m
nS 2X + mS 2Y n + m
< µX–µY < X − Y + t n+m−2,(1−c ) 2
n + m − 2 nm
n + m − 2 nm
IC para µX–µY si σX y σY son totalmente desconocidas
X − Y − (µ X − µ y )
S c2,X
n
+
S c2,Y
≈ tν*
Sc2, X Sc2, Y
Sc2, X Sc2, Y
< µX–µY < X − Y + t ν,(1− c ) 2
+
+
n
m
n
m
X − Y − t ν,(1− c ) 2
m
(valido aprox.)
IC para σ2X/σ2Y si µX y µY son conocidas
m∑ ( X i − µ X ) 2
σ 2X
m∑ ( X i − µ X ) 2
1
1
<
<
2
2
2
σY
n∑ ( Yi − µ Y ) Fn,m,(1+c ) / 2
n∑ ( Yi − µ Y ) Fn,m,(1−c ) / 2
∑ ( X i − µ X ) 2 mσ 2Y ~ F
n,m
∑ ( Yi − µ Y ) 2 nσ 2X
IC para σ2X/σ2Y si µX y µY son desconocidas
2
nS 2X (m − 1) σ 2Y S c,X σ 2Y
~ Fn–1,m–1
=
mS 2Y (n − 1) σ 2X S c2,Y σ 2X
*ν=entero más próximo a
(
Sc2, X
n + Sc2, Y
m
S c2,X
1
S c2,Y Fn−1,m−1,(1−c ) / 2
)
2
(
) (
)
<
S c2,X
σ 2X
1
<
2
2
S c,Y Fn−1,m−1,(1+c ) / 2
σY
 S2 n 2 S2 m 2 
 c, X

c, Y
 n − 1 + m − 1  . Si m y n son grandes, sustituir tν por una N(0,1).

