Determinar los caudales que aportan los depósitos A y B en el

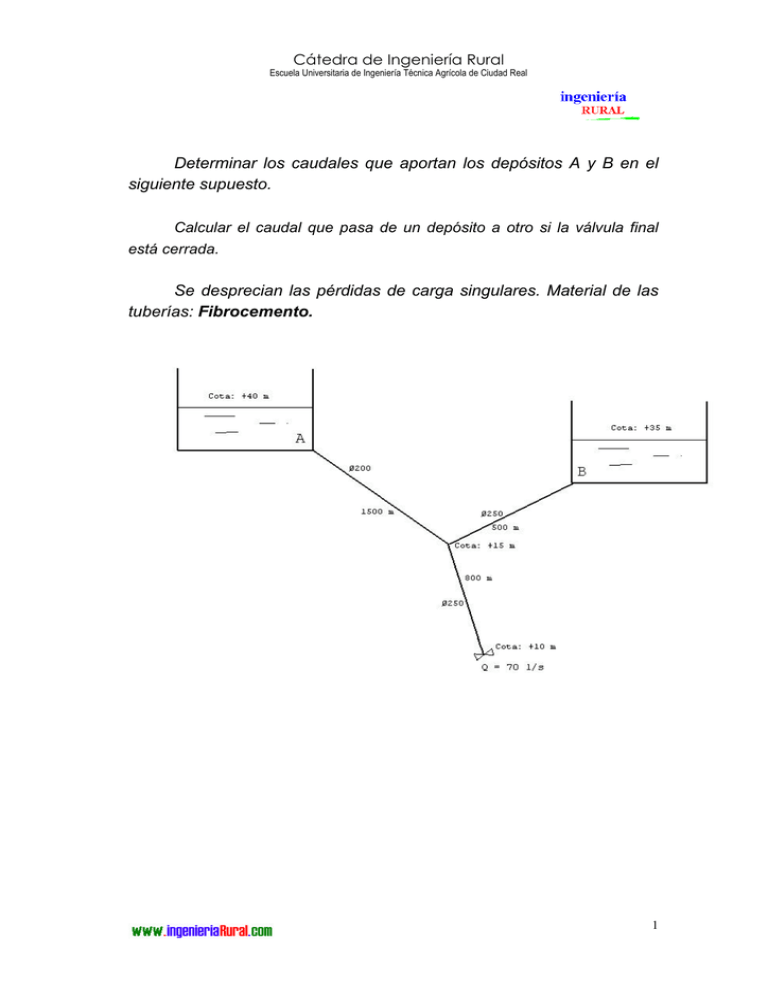
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Determinar los caudales que aportan los depósitos A y B en el
siguiente supuesto.
Calcular el caudal que pasa de un depósito a otro si la válvula final
está cerrada.
Se desprecian las pérdidas de carga singulares. Material de las
tuberías: Fibrocemento.
1
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
a) Determinar los caudales que aportan los depósitos A y B en el
siguiente supuesto.
La cota piezométrica es única (cada punto tiene UNA presión), luego
en D tienen que converger las líneas piezométricas trazadas desde los
depósitos A y B.
∇40
L.c.e.
A
∇35
L.c.e.
L.p.
hAD
hBD
B
25 m
20 m
x
D ∇15
Este ejercicio se resuelve por tanteos, ya que sólo sabemos que QA +
QB = 70 l/s y que la presión en D, PD/γ, que hemos llamado x, estará
comprendida entre 0 y 20 mca, puesto que la cota piezométrica en D estará
entre 15 mca (x=0) y 35 mca (x=20).
Para cada valor x de tanteo calcularemos QA y QB, y la solución se
obtendrá cuando QA + QB ≈ 70 l/s (0.07 m3/s).
h AD
0.56
⇒ Q A = 48.3 ⋅ D 2.68
AD ⋅ J AD
L AD
h
2.68
0.56
= BD ⇒ Q B = 48.3 ⋅ D BD
⋅ JBD
L BD
hAD = 25 – x
⇒ J AD =
hBD = 20 – x
⇒ JBD
¿ QA + QB ≈ 0.07 m3/s ?
2
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Tanteamos con x = 10 m.
hAD = 25 – 10 = 15 m ⇒ J AD =
15
= 0.01 ⇒ Q A = 0.049 m 3 /s
1500
hBD = 20 – 10 = 10 m ⇒ JBD =
10
= 0.02 ⇒ Q B = 0.131 m 3 /s
500
QA + QB = 0.18 m3/s > 0.07 m3/s
Hay que reducir el caudal, para lo cual hay que disminuir h y
aumentar PD/γ, es decir, aumentar x.
Entonces, ahora 10 < x < 20.
Después de varios tanteos, se obtiene x = 18.8 m.
hAD=25–18.8=6.2m ⇒ J AD =
6.2
= 4.13 ⋅ 10 −3 ⇒ Q A = 2.99 ⋅ 10 −2 m 3 /s
1500
hBD=20–18.8=1.2 m ⇒ JBD =
1.2
= 2.40 ⋅ 10 −3 ⇒ Q B = 4.01⋅ 10 −2 m 3 /s
500
QA + QB = 0.070 m3/s
Solución: El depósito A aporta 29.9 l/s y el depósito B 40.1 l/s.
3
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
b) Calcular el caudal que pasa de un depósito a otro si la válvula
final está cerrada.
∇40
L.c.e.
A
L.c.e.
hAD
L.p.
5m
hDB
∇35
Q
B
PD/γ
Q
D
∇15
La pérdida de carga total en el recorrido AB será de 40 – 35 = 5 mca.
hAD + hDB = 5 mca
JAD· LAD + JBD· LBD = 5
JAD· 1500 + JBD· 500 = 5 (1)
Por otra parte y lógicamente, el caudal que circule por el tramo AD
será el mismo del DB.
QAB = QAD = QDB
0.56
2.68
0.56
Q AB = 48.3 ⋅ D 2.68
AD ⋅ J AD = 48.3 ⋅ D DB ⋅ JDB
(2)
2 .68
0.56
0.200 2.68 ⋅ J0.56
⋅ JBD
AD = 0.250
 J AD 


 JBD 
0.56
 0.250 
=

 0.200 
2.68
= 1.82 ⇒
1
J AD
= (1.82)0.56 = 2.91⇒JAD= 2.91· JBD
JBD
Sustituyendo esta relación en (1):
4
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
2.91· JDB· 1500 + JDB· 500 = 5 ⇒ JDB = 1.03· 10-3
JAD = 3· 10-3
Y sustituyendo en una de las ecuaciones de (2), se obtiene que el
caudal que pasa de A a B es de 0.025 m3/s, es decir, 25 l/s.
5