Unidad II. Análisis de reactores ideales isotérmicos Elemento de

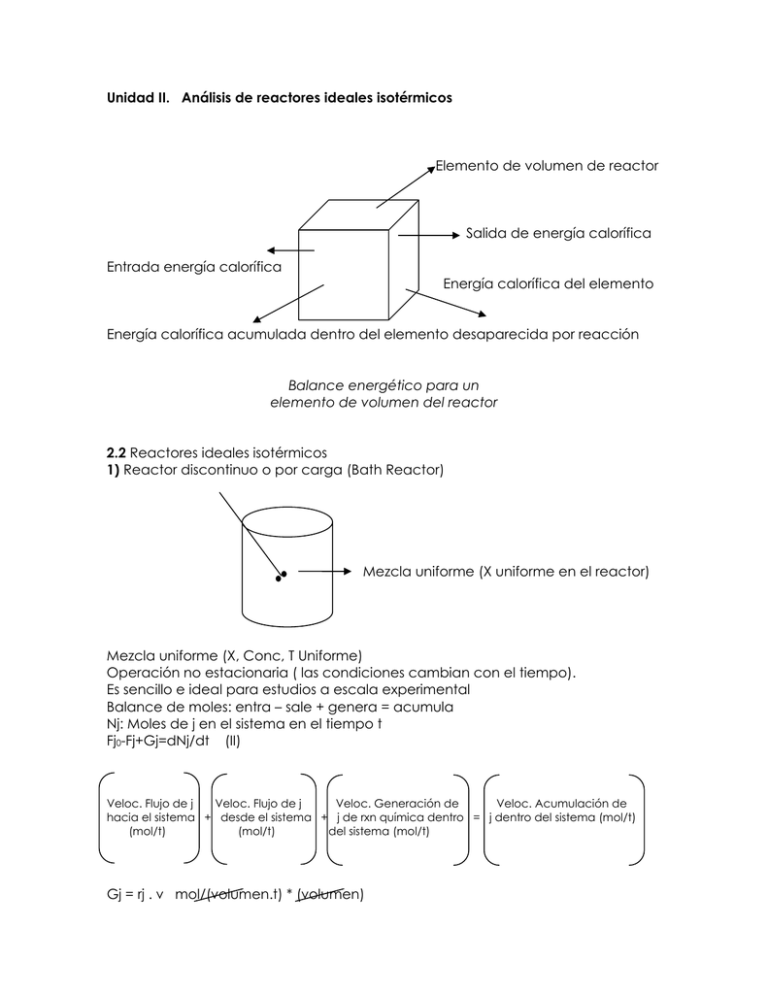
Unidad II. Análisis de reactores ideales isotérmicos
Elemento de volumen de reactor
Salida de energía calorífica
Entrada energía calorífica
Energía calorífica del elemento
Energía calorífica acumulada dentro del elemento desaparecida por reacción
Balance energético para un
elemento de volumen del reactor
2.2 Reactores ideales isotérmicos
1) Reactor discontinuo o por carga (Bath Reactor)
Mezcla uniforme (X uniforme en el reactor)
Mezcla uniforme (X, Conc, T Uniforme)
Operación no estacionaria ( las condiciones cambian con el tiempo).
Es sencillo e ideal para estudios a escala experimental
Balance de moles: entra – sale + genera = acumula
Nj: Moles de j en el sistema en el tiempo t
Fj0-Fj+Gj=dNj/dt (II)
Veloc. Flujo de j
Veloc. Flujo de j
Veloc. Generación de
Veloc. Acumulación de
hacia el sistema + desde el sistema + j de rxn química dentro = j dentro del sistema (mol/t)
(mol/t)
(mol/t)
del sistema (mol/t)
Gj = rj . v mol/(volumen.t) * (volumen)
Supongamos ahora que rj varía con la posición en el volumen V del
sistema. En el punto (1,rj1) rodeado por un volumen pequeño ∆V1, dentro del cual
la velocidad es uniforme, así:
∆Gj1 = rj1 . ∆V1 (I)
Gj =
=
(II)
Usando límites apropiados (M
∞, ∆V
0)
(III)
Gj =
Esta ecuación dice que rj es una función indirecta de la posición puesto
que las propiedades de los materiales que reaccionan (concentración,
temperatura) pueden tener diferentes valores.
Fj0 – fj +
=
(IV)
Esta es la ecuación general de balance de moles, de la cual podemos
partir para desarrollar las ecuaciones de diseño para los diversos tipos de
reactores industriales. Evaluando estas ecuaciones se pueden determinar el tipo
(por carga) o el volumen del reactor (flujo continuo) necesario para convertir una
cantidad dada de reactivos en productos.
En un reactor por carga, entra = sale = 0; la ecuación (IV) nos queda:
=
Si la mezcla es homogénea (uniforme) se saca rj de la integral,
= rj.V (V)
=
Si V = ctte:
Si P = ctte:
= rj
Nj = Cj . V
1 dNj
1 d (Cj.V ) dCj Cj dV
= rj ⇒
=
+
= rj
V dt
V dt
dt
V dt
Simplificando;
Para la especie A, la ecuación (V): −
dN A
= (− rA )V
dt
En función de la conversión X,
NAo .
Integrando:
t = NAo
Area
o
A V = ctte:
Area
o
Area
o
El tiempo es la medida natural de la velocidad del proceso, a continuación
se definirán tres términos de medidas adecuadas para el diseño de los reactores
ideales de flujo:
Tiempo espacial (τ): magnitud adecuada para el diseño de sistemas fluyente. Es el
tiempo necesario para que un volumen equivalente del reactor pase a través de
él.
;
(De la definición de concentración),
τ=
V
vo
Velocidad espacial (s): Es el número de veces que pasa el volumen equivalente
del reactor a través de él.
Tiempo medio de residencia ( t ): Es el tiempo que permanece el fluido en el
reactor.
t =
V
v
Reactores de Flujo Continuo.
2)Reactor de Flujo de mezcla completa, en estado estacionario (RTMC).
- Uso muy común en procesos industriales.
Reactor
- Se considera que las reacciones de
salidas son iguales a las condiciones
dentro del tanque.
- Mezcla uniforme; operación
Producto estacionaria.
Balance de moles:
De la ecuación general,
Acumulación = 0
Mezcla homogénea (no varía rj a lo largo del volumen del reactor),
NOTA: en los sistemas que se elijan mucho de lo ideal, la mezcla no será uniforme y se
recurrirá a otras técnicas de modelaje del diseño, como el tiempo de residencia.
Para la especie j = A:
En función de la conversión:
;
Como τ = CAo.V/FAo ;
En función de la concentración:
Si V=ctte: CA=CAo(1-XA)=CAo-CAoXA
Entonces,
Como τ = CAo.V/FAo :
3)Reactor de flujo en pistón, tubular (RFP).
Alimentación
A.∆Y= ∆V
Producto
Ventaja: Conversión X más alta por volumen V de todos los reactores.
Desventaja: Difícil controlar la temperatura T, ya que pueden presentarse
puntos calientes si la reacción es exotérmica.
-
Operación estacionaria
No hay variación radial de la concentración; varía continuamente en
dirección axial, a todo lo largo del reactor.
Balance de moles:
Acumulación = 0
Dividiremos imaginariamente el reactor en varios subvolúmenes ∆V, donde rj se
considera uniforme, situado a una distancia “Y” de la entrada del reactor,
Fj(y)
∆V
Fj(y)-Fj(y+∆y)+rj∆V=0
Fj(y+∆y)
Donde, Y: es la longitud del reactor.
rj : función indirecta de Y por la concentración.
∆V=A.∆y ; sustituyendo y rearreglando,
Para el reactante A,
−
dF A
= −r A
dV
En función de la conversión:
FA=FAo(1-XA)
dFA=-FAo.dXA
Sustituyendo,
En función de la concentración:
Si V=ctte: CA=CA0 - CA0X
dCA = -CA0.dX
dX = −
dCA
C A0
C
Af dC
V
1
A
=−
∫
FA0
C A0 C − rA
A0
C
Af dC
V
A
τ=
=− ∫
vO
r
−
A
C A0
Ejemplo.
(a)En un reactor discontinuo se planifica la conversión de A en R. La reacción se
efectúa en fase líquida; la estequiometría es A → R y la (–rA) es la indicada en la
tabla. Calcule el tiempo que tarda en reaccionar cada carga para que la
concentración descienda de CA0=1.3 mol/L a CAf=0.3mol/L
CA(mol/L)
-rA(mol/L.min)
0.1
0.1
0.2
0.3
0.3
0.5
0.4
0.6
0.5
0.5
0.6
0.25
0.7
0.10
0.8
0.06
1.0
0.05
1.3
2.0
0.045 0.042
(b) Calcule el tamaño del reactor de flujo en pistón para alcanzar la
concentración del 80% con una alimentación de 1000 mol A/h. (CA0=1.5 mol/L)
(c) Calcule el tamaño del reactor de mezcla completa necesario para alcanzar
la conversión del 75% con una alimentación de 1000 mol A/h. (CA0=1.2 mol/L)
(d) repetir (c) si se duplica el caudal de la alimentación a 2000 mol A/h (CA0=1.2
mol/L)
(e) repetir (c) si CA0=2.4 mol/L manteniendo la alimentación de 1000 mol A/h.
Solución
(a)RPC, fase líquida (V=ctte), A→R
T=?
CA0=1.3 mol/L
CAf=0.3 mol/L
; -rA=KCAn
Log (CA)
-1
-0.699
-0.5229
-0.3979
-0.3010
-0.2219
-0.1549
-0.0969
0
0.1139
0.3010
Log (-rA)
-1
-0.523
-0.3010
-0.2219
-0.3010
-0.6021
-1
-1.2219
-1.301
-1.3468
-1.3768
Sustituyendo en la ecuación anterior, por regresión lineal con el uso de su
calculadora:
Log K=-1.0210, entonces K=0.095
n= -0.068
Unidades de K:
(b) RFP, líquida (v=ctte)
V=?
X=0.8
CA0=1.5 mol/L
De la parte (a): –rA=0.095CA-0.68
Analíticamente, u=(1-X): du=-dx;
− 16.67mol / min (1.5mol / L )0.68 ⎡
(1 − 0.8)1.68 − 1⎤⎥
⎢
⎣
⎦
1.68⎛⎜ 0.095mol 1.68 / L1.68 . min ⎞⎟
⎝
⎠
V = 128.4 L
V=
(c) RFMC , V=?
-rA=0.095 CA-0.68
X=0.75
FA0=1000 mol/h*1h/60 min=16.67 mol/min
CA0=1.2mol/L
XC 0.68 (1 − X )0.68
V
X
A0
=
=
F A0 ( −r A )
0.095
V=58.03 L
(d) V=?
FA0=2000 mol/h=33.33 mol/h
(e) V=? CA0=2.4 mol/L
Reactor de lecho empacado (RLE).
Balance igual al del RFP,
-rA`:gmol/gcat.min
2.3 Análisis de sensibilidad.
1) Determinar la variable a controlar y su intervalo de operación
2) Determinar cuales son las perturbaciones al proceso o que afectan a la
variable a controlar.
3) Determinar el modelo matemático que correlaciona la interacción de la
variable la perturbación con la variable controlada.
4) Determinar los rangos de operación de cada perturbación.
5) Seleccionar la perturbación critica.
(variable a
controlar) XA
XA
95%
92%
89%
Vmín Vdes Vmáx
3%
V
Vdes: volumen deseado, el volumen de diseño
% Lim superior =
Vmáx − Vdes
* 100
Vdes
% Lim inferior =
Vmín − Vdes
* 100
Vdes