Ejercicios Tema 2 - Universidad de Oviedo

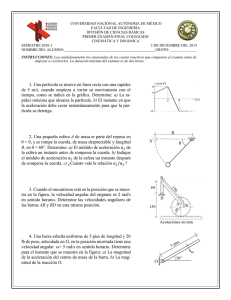
Departamento de Física
2
Mecánica y Termodinámica
Escuela Politécnica de Ingeniería de Gijón
UNIVERSIDAD DE OVIEDO
Curso 2013-4
1. Sabiendo que el vector de posición de un móvil es
 Pt2 

r t   P t i 
j
2
siendo P una constante, calcúlese:
a) La trayectoria del móvil.
b) Su velocidad y aceleración.
c) Las componentes intrínsecas de su aceleración.
d) El radio de curvatura de la trayectoria.

 


2
Solución: a) x  2 Py ; b) v  P i  Pt j , a  P j ; c) at  Pt

d)   P 1  t

2 32
1  t 2 , an  P
1 t2 ;
.
2. Una pelota se lanza verticalmente hacia arriba desde el suelo. Desde una ventana situada
a 9,8 m de altura con respecto al suelo una persona ve que la pelota pasa hacia arriba
delante de ella a una velocidad de 4,9 m/s. Tomando g = 9,8 m/s2:
a) ¿Con qué velocidad fue lanzada la pelota?
b) ¿Cuál fue su velocidad media desde que fue lanzada hasta que alcanzó la ventana?
c) ¿Qué altura alcanzará la pelota por encima del suelo?
d) ¿Cuánto tiempo tardará en alcanzar la máxima altura a partir del instante en el que pasa
por la ventana?
Solución: a) v0  14,7 m/s; b) vm  9,8 m/s; c) h = 11,025 m; d) t  0,5 s.
3. Un punto móvil describe una trayectoria parabólica de ecuación x  2 y de modo que la
proyección de la velocidad sobre el eje Ox vale 3 m/s. Determínense la velocidad y la
aceleración del punto en función del tiempo sabiendo que en el instante inicial se
encuentra en el origen de coordenadas.

 


Solución: v  3 i  9 t j , a  9 j .
2
4. Una partícula P desliza por la superficie de un cilindro vertical de radio R, girando en
torno al eje Oz a razón de    rad/s y elevándose sobre el plano Oxy una altura que
n
depende del tiempo según la ecuación z  m t , donde m y n son números reales. En el
instante inicial se encuentra en el punto de coordenadas cartesianas A (R, 0, 0). Hállese:
a) El valor de n para que la aceleración de P sólo tenga componente normal.
b) Para el valor anterior, las expresiones en coordenadas cilíndricas de la velocidad y la
aceleración de P.
c) El radio de curvatura y la ecuación horaria del movimiento.


 
m2
2
Solución: a) n = 1; b) v  R u  m uz , a   R u ; c)   R 
, s  R 2 2  m2 t .
R 2


5. Desde que un conductor percibe un obstáculo en la carretera hasta que empieza a frenar
transcurre un tiempo t R (tiempo de reacción). Suponiendo que los frenos producen una
aceleración constante a de sentido contrario a la marcha, obténgase la distancia (distancia
de frenado) que recorre un coche que viaja a velocidad v0 desde que el conductor percibe
el obstáculo hasta su completa detención.
Solución: d F  v0t R  v0 2a  .
2
23/09/2013
1
Departamento de Física
UNIVERSIDAD DE OVIEDO
2
Mecánica y Termodinámica
Escuela Politécnica de Ingeniería de Gijón
Curso 2013-4
6. Una barca de remos se orienta perpendicularmente a la orilla de un río que tiene una
anchura de 100 m. Si el remero puede impulsar la barca con una velocidad de 4 m/s con
respecto al agua y el río tiene una corriente de 3 m/s.
a) ¿A qué distancia aguas abajo de punto de partida estará la barca cuando llegue al lado
opuesto?
b) ¿En qué dirección deberá orientar la barca el remero para llegar al lado opuesto del río
en el punto situado justo enfrente del de partida?
c) Calcúlese el tiempo que se tarda en cada una de las dos travesías.
Solución: a) d = 75 m; b)   41,4º ; c) t1  25 s, t2  37,8 s
7. Un hombre de estatura h se aleja de una
farola encendida de altura H con
movimiento rectilíneo uniforme de
velocidad u. Hállense la velocidad y la
aceleración del extremo de su sombra.
H
h
Solución: v  Hu H  h ; a  0 .
x
8. La figura representa una lámpara
encendida, situada a una altura 2H sobre el
suelo. La varilla AB de longitud H gira
uniformemente con velocidad angular ω
partiendo de la vertical. Hállese la
velocidad de la sombra del extremo B de
la varilla,
a) cuando forma 45º con el suelo, y
b) cuando contacta con el suelo.



X
2H
B
H
2
Solución: a) v  8H 2  1 4  2 ;
b) v   H 2
A
9. La aceleración angular  de un péndulo satisface la ecuación   4 , siendo  el
ángulo que forma el hilo con la dirección vertical. Sabiendo que partiendo de la vertical
alcanza un ángulo máximo de /3 rad, hállense:
a) La velocidad angular del péndulo en función del ángulo girado .
b) La posición, velocidad y aceleración angulares en función del tiempo.
c) ¿Es un movimiento periódico? ¿Es un movimiento armónico simple?
2 2
π  9 2 ;
Solución: a)    
3
π
2π
4π
cos2 t  ,  t   
sen2 t  .
b)  t   sen 2 t  ,  t  
3
3
3
10. Un punto móvil describe una trayectoria circular de 20 cm de radio, con una aceleración
tangencial at  2v , donde v  vt  es la función velocidad escalar del móvil. Sabiendo
que en el instante inicial la velocidad angular es 0 = 5 rad/s, hállense la velocidad y la
aceleración angulares en función del tiempo.
Solución:  t   5 e
23/09/2013
2t
,  t   10 e
2t
.
2
11. Un volante de 4 m de radio se hace girar respecto a un eje horizontal mediante una cuerda
enrollada en su borde con un peso en su extremo. Si la distancia vertical recorrida por el
2
peso está dada por la ecuación x  40 t , donde x se mide en metros y t en segundos.
Calcúlense la velocidad angular y la aceleración angular del volante en función del
tiempo.
Solución:  t   20 t rad/s,  t   20 rad/s2.
12. Se considera un movimiento armónico simple de pulsación   1 rad/s y amplitud
A = 8 m.
a) Calcúlese en qué puntos coinciden los valores de la aceleración y de la velocidad
lineal.
b) Calcúlese en qué puntos coinciden los valores de la aceleración y de la elongación.
c) Represéntense gráficamente a  ax  y v  vx  .
Solución: a) x  4 2 m; b) x  0 m.
13. Se dispara un proyectil en una dirección que forma un ángulo  con la horizontal.
Calcúlese la velocidad que debe imprimírsele si se pretende alcanzar un objetivo situado a
una distancia d en la misma cota de nivel del lugar de disparo. ¿Cuál debe ser el ángulo
de inclinación para que, alcanzándose el objetivo, esta velocidad sea mínima?
Solución: v0 
gd
,   π 4 rad.
sen 2 
14. Un avión que viaja horizontalmente con una velocidad v0 deja caer un objeto. Calcúlese:
a) La ecuación de su trayectoria.
b) La velocidad del objeto en función del tiempo.
c) Las componentes intrínsecas de su aceleración en función del tiempo.
d) El radio de curvatura de su trayectoria en función del tiempo.
Solución: a) y  y0  5x 2 v02 ;
b) vt   v0  100t ;
2
c) at t   100t
2
v02  100t 2 , an t   10v0
d)  t   v02  100t 2 
32
v02  100t 2 ;
10v0  .
15. Se lanza un objeto A verticalmente hacia
arriba con velocidad inicial vA 0  30 m/s .
Al mismo tiempo, se lanza otro objeto B
horizontalmente desde una altura h, con
velocidad inicial vB0  12 m/s . Si la distancia horizontal que separa inicialmente
los objetos es xAB  24 m , hállese:
B
vB0
vA0
h
A
xAB
a) El tiempo que tardan en chocar los objetos.
b) El valor de la altura h.
Solución: a) t = 2 s , b) h = 60 m .
3/4
16. Las ecuaciones del movimiento de un objeto vienen dadas por las siguientes ecuaciones
(donde todas las magnitudes están expresadas en unidades del S.I.):
x  2t 2  1
y  3t
Hállese en el instante t = 1 s:
a) Las componentes intrínsecas de la aceleración.
b) El radio de curvatura de la trayectoria.
Solución: a) 𝑎 𝑇 = 3,2 m/s 2 , 𝑎𝑁 = 2,4 m/s2
b) 𝜌 = 10,42 m .
17. Las coordenadas cartesianas de la posición de una partícula están dadas, en el SI, en
función del tiempo por las siguientes ecuaciones:
x t   3t  5
y  t   4  2t 2
Hállense:
a) Las unidades de los coeficientes numéricos (2, 3, 4 y –5).
b) Las componentes tangencial y normal de la aceleración en el instante t = 1 s.
Solución: a) 3 m/s ; 5 m ; 4 m ; 2 m/s2 , b) 𝑎 𝑇 = 3,2 m/s2 ; 𝑎𝑁 = 2,4 m/s2 .
18. Un tren de 100 m de longitud acelera uniformemente desde el reposo. Si el extremo
inicial del tren pasa a 90 km/h frente a un trabajador ferroviario situado a 150 m del punto
de partida, ¿a qué velocidad pasará el extremo final del tren frente al trabajador?
Solución: 𝑣 = 116,2 km/h .
19. Una partícula móvil se desplaza por una guía circular. La función horaria del movimiento
viene dada por la expresión s = (⅓) t3 + t2 donde s se mide en metros y t en segundos.
Sabiendo que en el instante t = 3 s el módulo de la aceleración total vale 10 m/s2,
determínese el radio de la guía.
Solución: R = 37,5 m .
20. La aceleración de una partícula con movimiento rectilíneo está relacionada con la
velocidad mediante la siguiente ecuación, en el SI:
a  4v
Sabiendo que x = 0 m y v = 4 m/s en el instante inicial (t = 0), hállense:
a) La expresión de la velocidad de la partícula en función del tiempo.
b) La expresión de la posición de la partícula en función del tiempo.
Solución: a) 𝑣 = 4𝑒 −4𝑡 , b) 𝑥 = 1 − 𝑒 −4𝑡 .
21. La posición de una partícula que se mueve en el plano está dada por su vector de
posición:



r  sen 2t i  2 sen 2t  π 4 j
Hállense:
a)
El primer instante en que su velocidad tiene la dirección del eje Oy, y la posición que
ocupa entonces.
b) La velocidad con que se está acercando al origen de coordenadas en ese momento.
Solución: a) 𝑡 = 𝜋⁄4 s , 𝑟⃗ = 𝐢 + √2𝐣 m b) 𝑣𝑟 = −4/√3 m/s .
4/4