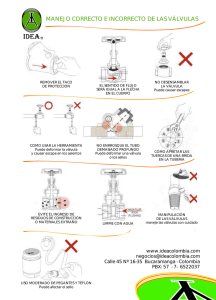
manual de practicas de laboratorio para perdidas en tuberias, de
Anuncio

MANUAL DE PRACTICAS DE LABORATORIO PARA PERDIDAS EN TUBERIAS, DE BANCO BASICO DE HIDRAULICA HM 150. TRABAJO PRACTICO EDUCATIVO QUE PARA ACREDITAR LA EXPERIENCIA EDUCATIVA EXPERIENCIA RECEPCIONAL PRESENTA: EZEQUIEL RIOS GÁRCIA ANTONIO PAREDES ORTEGA DIRECTOR DE TRABAJO RECEPCIONAL: ING. CESAR IGNACIO VALENCIA GUTIERREZ POZA RICA DE HGO, VERACRUZ SEPTIEMBRE 2010 AGRADECIMIENTOS A Dios Por prestarme la vida hasta este momento y poder ver culminada mi carrera, darme la fuerza que me hacía falta y la esperanza para no rendirme jamás. A mis padres y hermanos Quiero a gradecer a mis padres que creyeron en mí, brindándome su apoyo incondicional y animándome a seguir a delante, aun cuando en determinados momentos la situación no era muy favorable y a mis hermanos que me a nunca me dejaron solo y me dieron la confianza y el apoyo gracias a ustedes querida familia a los cuales quiero mucho. A mi esposa e hijos Gracias a Dios que me ha dado esta linda esposa, con la que he compartido bellos momentos y momentos difíciles. Gracias a ti mi amor por tu grande apoyo y palabras de aliento que han servido para seguir adelante, gracias a mi hijo David y a mi bebe que viene en camino porque han sido de gran bendición a mi vida y por ellos seguiré luchando hasta el final INDICE CAPITULO I…………………………………………………………………………..........… 1 INTRODUCCIÓN………………………………………………………….………………….. 2 JUSTIFICACIÓN………………………………………………….…………………….......... 3 TIPO Y NATURALEZA DEL TRABAJO……………………………………………………. 4 CARACTERISTICAS Y FUNCIONES ESENCIALES...………………….………………. 5 CAPITULO II……………………………………..………………………….………………... 6 1.0 DESCRIPCIÓN DEL EQUIPO……………………………………….…………………. 7 1.1 BANCO BASICO DE HIDRAULICA MODELO HM 150………….………………….. 7 1.2 SET DE PRUEBAS PARA PERDIDAS EN TUBERIAS Y ACCESORIOS DEL MODELO HM 150.11…………………………………………... 9 1.3 ACCESORIOS DISPONIBLES PARA EXPANSIÓN DEL BANCO BASICO DE HIDRAULICA PARA EXPERIMENTOS EN TUBERIAS................... 12 2.0 OPÉRACIÓN EN CONJUNTO DEL BANCO DE PRUEBAS……………............. 30 2.1 ACTIVIDADES PREVIAS A LA OPERACIÓN…………………………………..…… 30 2.2 OPERACIÓN NORMAL………………………………………………………………… 32 2.3 PARÁMETROS DE MEDICIÓN Y OBTENCIÓN DE DATOS……………………… 35 2.4 DETERMINACIÓN DEL CONSUMO DE ENERGÍA………………………………… 42 3.0 TEORÍA BÁSICA DE PÉRDIDAS EN SISTEMAS DE TRANSPORTE POR TUBERIAS……………………………………………………………………...... 45 3.1 MATERIALES PARA TUBERÍAS………………………………………........……...... 45 3.2 PÉRDIDAS DE CARGA POR ROZAMIENTO EN TUBERÍAS………..…………... 49 3.4 FÓRMULAS EMPÍRICAS PARA EL CÁLCULO DE PÉRDIDAS DE CARGA CONTINUAS EN TUBERÍAS………………………………………………………............. 69 3.5 PERDIDAS DE CARGA LOCALIZADAS ACCIDENTALES……………………… 78 4.0 PRÁCTICAS DE LABORATORIO PARA PÉRDIDAS EN TUBERÍAS Y ACCESORIOS HM-150.11………………….……………………………………………… 88 4.1 OPERACIÓN DEL BANCO BÁSICO DE HIDRÁULICA PARA PÉRDIDAS EN TUBERÍAS HM-150.11……………………………………………………………………… 89 4.2 DETERMINACIÓN DE PÉRDIDAS DE ENERGIA DE ENERGÍA A TRAVES DE UNA VALVULA DE COMPUERTA……………………………...…………………........... 94 4.3 DETERMINACION DE PÉRDIDAS DE ENERGÍA A TRAVES DE UNA VALVULA DE AGUJA……………………………………………………………………….. 98 4.4 MEDICIÓN DE CORRIENTE VOLUMÉTRICA CON TUBO VENTURI…………... 102 COSTOS……………………………………………………………….…………………….. 107 CAPITULO III..……………………………………………………………………………….. 108 APORTACIONES O CONTRIBUCIONES AL DESARROLLO…………………………. 109 BIBLIOGRAFIA………………………………………………………………………………. 110 CAPITULO I INTRODUCCION Actualmente existe una gran diversidad de procesos industriales que emplean grandes sistemas de tuberías, de las cuales podemos destacar el transporte de agua. En razón de ello, se han construido complejos sistemas de redes de tuberías, a gran escala, los que han crecido y se han automatizado cada vez más en los últimos años. La operación segura de estos sistemas es primordial debido a que se trata de un elemento vital y valioso. Sin embargo, y a pesar de todas las medidas de precaución que se tomen, siempre existe la posibilidad de pérdidas por diversos factores, tales como rajaduras en la pared de la tubería, defecto en las uniones, corrosión, desgaste, entre otras. Con la elaboración de este trabajo práctico educativo se pretende dar una visión amplia de todos aquellos factores que intervienen en el funcionamiento de las perdidas en tuberías, así como también crear un criterio para el entendimiento de los problemas generados en un sistema de fluidos. JUSTIFICACION Es de nuestro conocimiento que mediante las perdidas en tuberías se ha estado logrando a través del tiempo el mejoramiento y la optimización en la explotación y transformación de los recursos que en sus diversas modalidades nos ofrece la naturaleza. Este tema fue elegido por la importancia que representa la elaboración de prácticas realizadas en el laboratorio en base a los conocimientos que tenemos de determinados fluidos, encontrando como el más común el agua. De esta manera se logrará que los conocimientos obtenidos dentro de las aulas sean enriquecidos mediante la realización de prácticas de laboratorio. Este trabajo práctico educativo surge también de la necesidad de que la Facultad de Ingeniería Mecánica Eléctrica, tenga un equipo experimental para la materia de sistema de transporte de fluidos TIPO Y NATURALEZA DEL TRABAJO En la actualidad la tecnología ha avanzado eficientemente y por lo cual los niveles de competitividad a nivel empresarial exigen cada vez más y mayores conocimientos enfocados a optimizar los procesos. Por lo anterior, la realización de este trabajo práctico educativo tiene como objetivo conocer los diversos factores que influyen en el funcionamiento de las pérdidas de tuberías, así como también los conocimientos necesarios para su funcionamiento. CARACTERICAS Y FUNCIONES ESENCIALES Con este trabajo práctico educativo se podrá mostrar un entendimiento sencillo de las perdidas en tuberías. Que el estudiante pueda entender mejor los fenómenos que se presentan en el sistema de transporte de fluidos, mediante las prácticas de laboratorio con el modelo HM 150. El siguiente trabajo tiene como característica ser un trabajo práctico educativo para estudiantes de ingeniería en temas relacionados al sistema de transporte de fluidos. La función esencial de este trabajo práctico educativo es el de cumplir con los siguientes objetivos: Describir los diferentes tipos de pérdidas tanto primarias y secundarias que se presentan en los diversos sistemas de tuberías. Entender de manera fácil porque se presentan las pérdidas en tuberías a si como en sus accesorios. Dar a conocer el comportamiento variable de los fluidos a través de las tuberías. Que el estudiante comprenda los fenómenos que se presentan en los sistemas de transporte de fluidos, mediante las prácticas de laboratorio. . CAPITULO II 1.0 DESCRIPCIÓN DEL EQUIPO. 1.1 BANCO BASICO DE HIDRAULICA MODELO HM 150. Figura 1 Accesorios del Banco Básico de Hidráulica Modelo HM 150 1.-Depósito de medición volumétrico con recorrido de medición como canal abierto 2.-Depósito 3.-Válvula de purga 4.-Bomba centrífuga 5.-Válvula para ajustar el caudal 6.-Tubo de cristal con escala para leer el nivel del agua 7.-Caja de distribución 8.-Tubo de rebose 9.-Válvula de salida El suministro de agua tiene lugar mediante el módulo básico HM 150 de técnica de corrientes o a través de la red del laboratorio. Con el modelo HM 150 puede establecerse un circuito cerrado de agua. El Banco Básico de Hidráulica HM 150 junto con los amplios accesorios cubre un amplio espectro de ensayos de la hidromecánica y es un equipo ideal para laboratorios de hidromecánica. El módulo básico contiene una bomba con mecanismo estrangulador, un depósito y un dispositivo medidor del caudal volumétrico y abastece a todos los accesorios de la serie HM 150. La pieza superior del módulo básico es de GFK (Compuesto de fibra de vidrio). Todos los accesorios se colocan sobre esta pieza. Un recorrido de medición integrado sirve para experimentar con vertederos de aforo (medición del caudal de paso) en canales abiertos. La medición del caudal de paso tiene lugar en un depósito de medición dividido en dos con volúmenes definidos. Des este modo son posibles mediciones exactas tanto de caudales mayores como menores. Una escala colocada por fuera permite una lectura exacta de la cantidad de agua. El depósito de medición está empalmado a través de una válvula de compuerta al depósito de reserva. Una abertura en la pieza superior con tubo de rebose impide que el agua se sobre. Un motor eléctrico impulsa la bomba centrífuga, que transporta el agua hacia arriba, en donde pueden realizarse los diferentes experimentos a través de un acoplamiento de conexión. Todos los materiales elegidos garantizan la mayor protección posible contra la corrosión. 1.2 SET DE PRUEBAS PARA PERDIDAS EN TUBERIAS Y ACCESORIOS DEL MODELO HM 150.11. Figura 2 Set de Pruebas Para Pérdidas en Tuberías Modelo HM 150.11 El banco básico de hidráulica HM 150.11 permite realizar experimentos para la medición de caudal y de presión y cálculos de pérdidas de corriente y transcursos de presión en tubos y elementos de tubería especiales. En concreto pueden examinarse los siguientes temas: Análisis acerca de las pérdidas de presión en tuberías y accesorios. Influencia de la velocidad de corriente sobre la pérdida de presión. Pérdidas de presión y curvas características de apertura de los órganos de bloqueo. Determinación de los coeficientes de resistencia. Funcionamiento y principio de diferentes procedimientos de medición de caudales. Comparación entre el cálculo y el experimento. El equipo está compuesto de un bastidor de tubo de acero cuadrado con una pared posterior recubierta de polvo. Sobre esta pared se ha montado el trayecto de tubo con trozos parciales bloqueables individualmente. Además, en la pared posterior se han fijado dos manómetros de nivel con tuercas moleteadas en cruz. Los manómetros pueden montarse en dos posiciones en la pared posterior. El trayecto de medición desplazable sirve como alojamiento para los diferentes objetos de medición. Figura 3 Accesorios del Set de Pruebas Para Pérdidas en tuberías 1.-Bastidor de tubo de acero con patas con baldosa 2.-Pared posterior 3.-Grifos esféricos para bloquear los tramos parciales 4.-Camaras anulares con boquillas de toma de presión 5.-Manometro de tubo de nivel 6.-Trayecto de medición desplazable 7.-Medicion de caudal de los objetos de medición 8.-Organos de bloqueo de los objetos de medición 9.- Entrada (oculta) 10.-Evacuaciones Trayectos de medición 1 a 6 1.3 ACCESORIOS DISPONIBLES PARA EXPANSIÓN DEL BANCO BASICO DE HIDRAULICA PARA EXPERIMENTOS EN TUBERIAS. El banco de pruebas HM 150 es la base para varios experimentos, en el caso de este trabajo funciona en conjunto con el banco de pruebas HM 150.11para determinar perdidas en tuberías en serie y paralelo, en este punto se menciona algunos otros bancos de prueba que funcionan en conjunto con el HM 150 para diversas practicas. HM 150.110 BANCO EXPERIMENTAL HIDRODINAMICA APLICADA Figura 4 Banco Experimental Hidrodinámica Aplicada Modelo HM 150.110 Figura 5 Accesorios del Banco Experimental Hidrodinámica Aplicada HM 150.110 1.- Caja de distribución 2.- Deposito de agua 3.-Bomba sumergida 4.-Objetos de medición recambiables 5.- Diversos tramos de medición 6.-Camaras anulares para la medición de presión 7.- Manómetro de tubo de nivel 8.- Grifos de evacuación 9.-Flujometro flotador 10.-Manómetrosextuplo 11.-Registro de presión diferencial 12.-Termómetro 13.-Válvula reguladora de asiento oblicuo DESCRIPCIÓN El puesto de ensayo HM 110 permite ensayos básicos sobre la teoría del flujo. Composición esquematizada del ensayo sobre un carro móvil de laboratorio. Gracias al circuito cerrado del agua, el puesto de ensayos es particularmente idóneo para la aplicación en locales de formación y cursillos. El sistema contiene un flujómetro flotador, un registrador electrónico de la presión diferencial y otros dispositivos para medir la presión. Como objetos de medición sirven diferentes tramos de tubo y elementos integrables de los cuales 5 representan diferentes suplementos de tubo como, ejemplo: válvula de membrana o filtro depurador. A fin de poder hacer visible la función, 3 de los objetos de medición son de plexiglás, representan tubo Venturi, tubo Pitot, diafragma, respect., boquilla de medición. L a conexión de los puntos de medición y registradores de presión se realiza mediante mangueras con acoplamientos rápidos. Contenido didáctico / Ensayo Mediciones de la presión y velocidad con el tubo Pitot Mediciones con el flujo con boquilla y diafragma Investigaciones en el valvulaje: medición comparativa de la caída de presión, altura de pérdida y caudal en función del grado de apertura Investigaciones en las líneas de tubo: caudal de tubo con y sin fricción, estrechamiento de tubo, ampliación de tubo, codo y arco. Dimensiones y pesos del Banco Experimental Hidrodinámica Aplicada Modelo HM 150.110 LxAnxAl=2000x780x1900mm Peso aproximado 150 kg CONEXIONES 220V, a 60 Hz HM 111 MODULO DE ENSAYOS RED EN TUBERIAS Figura 6 Modulo de Ensayos Red en Tuberias HM 111 Figura 7 Accesorios del Modulo de Ensayos Red en Tuberias HM 111 1.-Panel de conservación para los elementos de empalme 2.-Depósito 3 Bomba sumergida 4.-Escala graduada para la medición del caudal 5.-Depósito de medición 6.-Manómetro de tubitos, mercurio 7.-Manómetro de tubitos, agua 8.-Red de tuberías 9.-Armario de distribución 10.-Válvulas de admisión DESCRIPCIÓN Un problema muy extendido en la construcción de tuberías es la determinación de la presión y caudal en sistemas complejos de líneas. El módulo de ensayos HM 111 Redes permite la estructuración y la investigación de diferentes sistemas de líneas de tuberías así como, por ejemplo, la distribución en serie y paralela de tubos, sus ramificaciones y confluencias. En analogía a la ley de Kichhoff en la teoría de la electricidad, la presión en el interior de la línea de tuberías corresponde a la presión; las pérdidas de presión, a la resistencia. Pueden realizarse análisis de los nudos. Los sistemas de tuberías se confeccionan en la parte superior del módulo de ensayos con los tubos y elementos de empalme suministrados. El módulo de ensayo tiene un circuito de agua cerrado con depósito de alimentación y bomba así como un depósito para la medición volumétrica del caudal. Para las mediciones de presión se incluyen 2 manómetros de tubito con diferentes rangos de medición. Contenido didáctico / ensayos Registro de una curva de calibración para los diferentes tramos de tubería: pérdida de presión a través del caudal de aire Distribución paralela de tubos (abierto/cerrado) Distribución en serie de tubos Distribución combinada en serie y paralelo Investigación anular (alimentador) Medición de la presión diferencial Perdida de presión de los diferentes elementos Dimensión y pesos del Modulo de Ensayos Red en Tuberias HM 111 LxAnxAl: 1800 x 800 x 1.600 mm Peso: aproximado 160 kg CONEXIONES 220V, a 60Hz HM 112 BANCO EXPERIMENTAL HIDRODINAMICA/PC Figura 8 Banco Experimental Hidrodinámica/pc HM 112 Figura 9 Accesorios del Banco Experimental Hidrodinámica/pc HM 112 1.- Caja de distribución 2.- Depósito 3.- Bomba 4.- Manómetro de tubo de nivel 5.- Armario de distribución con indicadores digitales 6.- Registrador electrónico de la presión 7.- Objeto de medición 8.- Tramo de medición 9.- Manómetro séxtuplo 10.- Termómetro 12.- Válvula mariposa 13.- Flujómetro DESCRIPCÓN El banco de ensayos HM 112 permite realizar ensayos básicos sobre la teoría del flujo. La composición del ensayo está esquematizada sobre un carro de laboratorio. Mediante el equipamiento con un circuito cerrado del agua, el banco de ensayos es particularmente idóneo para la aplicación en locales de formación, cursillos y aulas. El sistema contiene sensores de flujo y de la presión que permiten procesar posteriormente sobre PC los valores medidos. Como objetos de medición sirven diferentes tramos de tubo y elementos integrables de los cuales 5 representan diferentes suplementos de tubo como, p. ej., válvula de membrana o recogelodos. 3 objetos de medición son de plexiglás y representan tubo venturí, tubo Pitot, diafragma, respect., boquilla de medición. La tarjeta de registro de los datos de medición y software que incluye el suministro permite la indicación y evaluación en PC de los datos medidos. Contenido didáctico / Ensayos Mediciones de presión y velocidad con tubo Venturi/Pitot Mediciones de flujo con boquilla y diafragma Investigaciones en el valvulaje: medición comparativa de la caída de presión, altura de pérdida y caudal en función al grado de apertura Investigación en las líneas de tubo: Caudal de tubo con fricción, estrechamiento de tubo, ampliación de tubo, codo y arco, coeficientes de resistencia Dimensiones y pesos del Banco Experimental Hidrodinámica/pc HM 112 LxAnxAl: 2000 x 780 x 1900 mm Peso aproximado 155 kg Conexiones 230V, a 60Hz HM 120 EQUIPO DE DEMOSTRACION PÉRDIDAS EN TUBERIAS Figura 10 Equipo de Demostración Pérdidas en Tuberías HM 120 Figura 11 Accesorios del Equipo de Demostración Pérdidas en Tuberías HM 120 1.-Panel de demostración 2.-Toma de agua 3.-Tramo de tubo para ensayo (10 unidades) 4.-Cámara anular para medición de la presión 5.-Desagüe 6.-Manguera de conexión 7.-Flujómetro flotador 8.-Codo 9.-Registrador de la presión diferencial 10.-Manómetro doble 11.-Tabla de manómetro 12.-Tubo acodado 13.-Codo DESCRIPCIÓN La distribución del ensayo está esquemáticamente dispuesta sobre un panel de demostración. El panel se encuentra sobre un bastidor móvil de laboratorio y es por ello de flexible aplicación. Para el servicio se requiere simplemente una toma de agua fría y un desagüe. Para los estudios en la tubería se tienen a disposición 10 tramos de tubo diferentes en que se encuentran tomas de medición con cámaras anulares. Las tomas de medición se conectan mediante mangueras con los correspondientes equipos de registro. Para los ensayos pueden seleccionarse tuberías únicas con mangueras de conexión. Para mediciones de la presión se dispone de manómetro doble, tabla de manómetro y un registrador electrónico de la presión diferencial. El caudal de paso se indica en un flujómetro flotador. Se incluye unas instrucciones de ensayo con amplia representación de la base teórica Contenido didáctico / Ensayos Aprender las mediciones de presión, mediciones de la presión diferencial Efecto del diámetro del tubo Efecto de diferentes materiales y rugosidades de la superficie Efecto de la velocidad del caudal Pérdida de presión en arcos, esquinas y codos Pérdida de presión en modificaciones de la sección transversal Determinación de coeficientes de resistencia Líneas características de apertura de diferentes válvulas Comparación entre experimento y cálculo Dimensiones y pesos del Equipo de Demostración Pérdidas en Tuberías HM 120 LxAnxAl: 2250 x 700 x 1800 mm Peso: aproximado 100 kg Conexiones Toma de agua fría 1.5bar HM 122 BANCO DE PRACTICAS PERDIDAS POR CIRCULACION Figura 12 Banco de Prácticas Perdidas por Circulación HM 122 Figura 13 Accesorios del Banco de Prácticas Perdidas por Circulación HM 122 1.-Bastidor de laboratorio móvil 2.-Contador de agua 3.-Tramo de medición con diferentes objetos de medición transparentes 4.-Depósito con bomba sumergid 5.-Tramo de medición con diferente valvulaje de cierre 6.-Manómetro de tubo de nivel 7.-Armario de distribución 8.-Registrador de presión diferencial 9.-Manómetro 10.-Tramo de medición con diferentes codos y ángulos 11.-Diferentes tramos de medición 12.- Cámara anular, 13 Flujómetro Contenido didáctico / Ensayos Caudal de tubo laminar y turbulento con fricción Definición del índice de fricción del tubo Coeficientes de resistencia de codos, arcos y ángulos Definición de la pérdida de presión en valvulaje de tubería Medición del caudal con boquilla/diafragma Mediciones de la corriente volumétrica con el tubo Pitot Mediciones de la corriente volumétrica con el tubo venturí Comparación mutua entre diferentes métodos de medición Dimensiones y pesos del Banco de Prácticas Perdidas por Circulación HM 122 L x An x Al: 2740 x 620 x 1800 mm Peso aproximado 275 kg Conexiones 220V, a 60Hz HM 125 BANCO DE PRÁCTICAS PÉRDIDAS EN TUBERIAS Figura 14 Banco de Prácticas en Tuberías HM 125 Figura 15 Accesorios del Banco de Prácticas en Tuberías HM 125 1.- Bastidor de laboratorio móvil 2.-Cámara anular para la medición de la presión 3.-Tramos de tubo de ensayo 4.-Medidor de presión diferencial 5.-Manómetro doble 6.-Flujómetro flotador 7.-Grifos de bola 8.-Caja de distribución 9.-Depósito de reserva DESCRIPCIÓN El puesto de ensayos para la inspección de pérdidas de tuberías es un montaje experimental cerrado en sí mismo. Mediante el montaje en un bastidor de laboratorio móvil y el circuito de agua cerrado con depósito de reserva y bomba, el puesto de ensayos es de aplicación flexible. Para las inspecciones en tuberías hay a disposición 8 tramos de tubo diferentes, que están equipados con cámaras anulares con conexiones de medición para las mediciones de la presión. Para los ensayos pueden seleccionarse individualmente las tuberías con grifos de bola. Para medición de la presión hay a disposición manómetros multitubos dobles y un medidor de presión diferencial electrónico accionado por pila. El caudal se indica en un flujómetro flotador. Se entregan unas instrucciones de ensayo con representación detallada del trasfondo teórico. Contenido didáctico / Ensayos Aprender mediciones de la presión, mediciones de la presión diferencial Efecto del diámetro de tubo Efecto de diferentes materiales y asperezas superficiales Efecto de la velocidad de corriente Pérdidas de presión en codos y arcos Pérdidas de presión en modificaciones de la sección transversal Determinación de coeficientes de resistencia Comparación entre experimento y cálculo Dimensiones y pesos del Banco de Prácticas en Tuberías HM 125 LxAnxAl: 1520 x 750 x 1950 mm Peso: aproximado 95 kg Conexiones 220V, a 60Hz 2.0 OPERACIÓN EN CONJUNTO DEL BANCO DE PRUEBAS. 2.1 ACTIVIDADES PREVIAS A LA OPERACIÓN. 2.1.1 Medidas de seguridad. Antes de realizar cualquier actividad con el banco de pruebas HM 150 o alguno de sus accesorios de expansión es necesario tomar las medidas de seguridad recomendadas a continuación: El banco de pruebas como cualquier otro equipo con el tiempo y uso se va deteriorando dependiendo del manejo y mantenimiento que se le dé a este, en caso de deterioros visibles (por ejemplo cables eléctricos deteriorados), no poner el aparato en servicio en ningún caso. En caso de estar ya en servicio, desconectar inmediatamente. Cuidar siempre de que las partes conductoras de tensión del equipo no entren en contacto con agua. Poner el equipo en servicio sólo en recintos secos. Los recintos deben están libres de humos, vapor, niebla etc. Si se guarda el equipo con agua, tiene que tomarse en cuenta que no se puede quedar en esas condiciones por varios días ya que el agua tiende a enrarecerse y por tanto puede dañar al equipo. Por eso lo recomendable es cambiar el agua periódicamente y limpiar el equipo adecuadamente. No poner en funcionamiento la bomba centrífuga sin agua. Antes de la puesta en funcionamiento del equipo todas las personas que lo manejan deben instruirse en el funcionamiento y el manejo de éste. 2.1.2 Puesta en funcionamiento. Leer previamente la practica a elaborar. Llenar el depósito de reserva con agua limpia hasta que se vea el agua en la mirilla. Establecer el abastecimiento de tensión 120 V,60 Hz Asegurarse de que el botón de paro de emergencia esté sacado. Empalmar la manguera en la salida del depósito de medición y unir con el tubo de cristal. Conectar el interruptor primario Abrir completamente la válvula para el ajuste del caudal Conectar la bomba y abrir lentamente el grifo principal del modelo HM 150 Establecer la unión de mangueras entre el HM 150 y el equipo. Abrir el desagüe HM 150 Asegurarse de que no tenga fugas de agua el equipo en cada unión de las tuberías. 2.2 OPERACIÓN NORMAL. Es necesario realizar una serie de operaciones antes de la puesta en marcha del banco básico HM 150. Para que ello se pueda concretar rápida y exitosamente, es muy importante reunir todos los recursos necesarios y seguir un estricto orden en las actividades que se proponen a continuación: Inspección preliminar del sistema. Operaciones iníciales. Llenado del depósito de reserva. Inicio del abastecimiento al sistema de distribución. La puesta en marcha ha concluido. A continuación, una breve explicación de cómo orientar cada uno de estos pasos dentro del instructivo de operación. 2.2.1 Inspección preliminar. Tiene como objetivo evaluar el estado de las operaciones realizadas en banco de pruebas de hidráulica del modelo HM 150. Debe ponerse especial atención en los siguientes aspectos: Presencia visual de daños. Funcionamiento de válvulas, compuertas y equipos. Existencia de reactivos, materiales y personal requerido para iniciar la operación del sistema. 2.2.2 Operaciones iníciales. Antes del llenado del modelo HM 150, deben efectuarse las siguientes labores: Limpieza general del modelo, que debe quedar libre de polvo o de residuos de cualquier otra impureza que signifique peligro de contaminación para la práctica a realizar. Calibración y revisión detallada de todos los accesorios que componen al banco de pruebas. Preparación de la solución de la prueba y cualquier otra sustancia química requerida en cada caso específico. Medición de los parámetros básicos para control de procesos. Una vez concluidas las operaciones de puesta en marcha, el banco básico de hidráulica HM 150 entra en la etapa denominada operación normal. La operación normal se define como todas las actividades destinadas a que el banco básico de hidráulica HM150 produzca el caudal para el cual fue diseñado con la calidad estipulada por las normas correspondientes. Estas actividades involucran la medición de caudal, medición de parámetros básicos como turbiedad. Este control de los procesos debe efectuarse por lo menos cada cuatro horas. Operación especial. Cuando por alguna causa, el banco básico HM 150 debe suspender la práctica, parcial o totalmente, se dice que la operación es especial. Esto significa que durante determinado lapso (corto o largo) la producción de agua se verá disminuida. Es importante efectuar una adecuada programación de las labores de operación especial. Las principales actividades que se clasifican dentro del concepto de operación especial son las siguientes: 1.-Limpieza de estructuras mayores. 2.-Operaciones de mantenimiento correctivo en el equipo. 3.-sustitución de válvulas. 4.-reparación de fugas. 5.-reparación o sustitución de equipos dosificadores y otros equipos. 2.2.3 Llenado del depósito de reserva. Para las prácticas en el equipo HM 150 a si como en sus accesorios de expansión, en este caso el modelo HM150.11 el agua a usarse debe de ser purificada para no causar incrustaciones en las tuberías y accesorios. La capacidad nominal del depósito de reserva es de 170 litros, no hay necesidad de llenar el depósito al máximo, por recomendaciones del equipo este puede trabajar con un mínimo de 120 litros, por lo cual lo más recomendable es trabajar dentro de este rango. 2.2.4 Inicio del abastecimiento al sistema de distribución. Después de haber llenado el depósito de reserva de agua con el volumen recomendado, se deben tomar las medidas de seguridad necesarias para la puesta en funcionamiento de la bomba, ya que esta, es la que abastecerá la línea de distribución del sistema para realizar las prácticas. 2.3 PARAMETROS DE MEDICION Y OBTENCION DE DATOS. Los parametros de medición que se obtienen del equipo de forma directa es la presión (presión en un punto y diferencias de presión) y el flujo volumetrico. A continuacion se describira el proceso de obtencion de estos datos. 2.3.1 Medicion de Presión. Con el manómetro doble pueden medirse en milímetros (mm) de columna de agua tanto las presiones diferenciales como también las sobrepresiones, que pueden convertirse en función de la presión de aire atmosférica en las presiones absolutas. Figura 16 Manómetro de Columna doble El rango de medición asciende de 0 a 1000 mm de columna de agua. El manómetro está compuesto de dos tubos de nivel de vidrio con una escala en mm de metal. Ambos tubos de nivel están unidos entre sí en su extremo superior y tienen una válvula de purga común. Con la válvula de purga cerrada se mide la presión diferencial, con la válvula de purga abierta se mide la sobrepresión. Los puntos de medición se conectan a los acoplamientos rápidos de manguera autoblocantes en los extremos inferiores de los tubos de nivel. Cada tubo de nivel dispone de una válvula de desagüe en el extremo inferior. Medición de la presión diferencial. En este proceso, la válvula de purga está cerrada. Encima de ambas columnas de agua se forma un colchón neumático con la presión como se muestra en la figura 17. Figura 17 Formación del colchón neumático De esta manera se obtienen los siguientes valores para las presiones a medir y : La presión diferencial asciende entonces a: La presión se elimina, lo que da lugar a: con Mediante la presión puede ajustarse el punto cero para la medición de la presión diferencial. Para un margen de medición máximo resulta conveniente situar el punto cero, o bien, el valor medio en el centro de la escala de medición De esta manera resulta el siguiente valor para la presión del colchón neumático: La presión se ajusta mediante la válvula de purga. Medición de la presión absoluta. Para medir la presión absoluta debe abrirse la válvula de purga y determinar la sobrepresión frente a la atmósfera. La presión corresponde a la presión de aire atmosférica . En este proceso debe tenerse también en cuenta la altura entre el punto de medición y el punto cero del manómetro, por lo tanto: = + Figura 18 Medición de la presión absoluta Conexión del manómetro y manejo. Conectar el manómetro a los puntos de medición deseados mediante las mangueras con los acoplamientos rápidos autoblocantes. Abrir el grifo esférico del desagüe. Conectar la bomba en el HM 150 para el abastecimiento de agua a través de la tubería del HM 150.11 Purga del manómetro. Cerrar la válvula de purga superior. Abrir ambas válvulas de desagüe inferiores. Abrir lentamente el grifo esférico en la afluencia del trayecto de tubo a medir. Figura 19 Purga del manómetro El trayecto de tubo y las mangueras de unión se purgan mediante una corriente de agua potente. Cuando no queden burbujas de aire en las mangueras de unión: Cerrar el trayecto de tubo del desagüe. Cerrar lentamente ambas válvulas de desagüe inferiores al mismo tiempo. Prestar atención a que ambas columnas de agua asciendan deforma proporcionada y que no se produzca ningún derrame entre los tubos de nivel Figura 20 Cierre del tubo del desagüe y cierre de válvulas inferiores. Ajuste del punto cero. Para garantizar el máximo margen de medición, el punto cero del manómetro debe encontrarse en el centro de la escala. Cerrar el trayecto de tubo del desagüe, el caudal es igual a cero. El nivel es el mismo en ambos tubos de medición. Ajustar con cuidado el nivel con la válvula de purga al centro de la escala. Figura 21 Ajuste del punto cero Con la válvula de purga sólo puede regularse hacia arriba el nivel. Cuando el nivel es excesivo, debe vaciarse la red de tubería. Entonces se requiere una nueva purga, antes de poder ajustar un punto cero más bajo. Realización de la medición. Regular el caudal deseado mediante el grifo de entrada. Leer la presión diferencial como diferencia de altura entre ambas columnas de agua. En caso de un indicador inestable debe estimarse el valor medio. En caso de las mediciones de la presión diferencial no importa tanto la exactitud absoluta, sino que las lecturas resultan ser reproducibles. La presión diferencial puede aumentar con un caudal grande hasta tal punto, que el agua rebasa por la línea de conexión superior al tubo de medición con menor presión. En caso necesario debe volver a ajustarse el punto cero. La medición de la presión diferencial tiene lugar siempre con la válvula de purga cerrada. Figura 22 Medición de la presión diferencial Terminación de la medición. Tras la finalización de la medición debe cerrarse el trayecto de tubo del desagüe. Desconectar la bomba en HM 150. Abrir completamente el trayecto de tubo de trayecto de tubo de afluencia. Abrir la válvula de purga y ambas válvulas de desagüe. El manómetro se va vaciando y el trayecto de tubo está sin presión. Figura 23 Apertura de la válvula de purga y de desagüe para calcular medición 2.3.2 Obtención del flujo volumétrico. Para obtener el flujo volumétrico enviado por la bomba hacia el sistema de distribución se requiere de un cronometro para determinar el tiempo t de subida de la altura de la columna del agua de 20 a 30 litros, esta columna se encuentra en la parte posterior del modulo HM 150, antes de accionar la bomba se debe cerrar la válvula de corredera en la salida del depósito de medición a si el agua fluirá hacia el depósito de medición, pudiendo leer el volumen y el tiempo de subida de este y aplicando la formula: Donde: Q es el gasto en ó V es el volumen medido de la columna en litros ó . t es el tiempo de llenado de la columna de agua en segundos 2.4 DETERMINACION DEL CONSUMO DE ENERGIA. Como todo equipo mecánico para llevar a cabo su operación, en este caso, el banco de pruebas HM 150 necesita de energía para alimentar al sistema. El motor eléctrico de la bomba que será la encargada de suministrar el agua al modulo de pruebas HM 150.11 es el responsable del consumo de esta energía eléctrica. El banco de pruebas HM 150 contiene una placa de datos donde se muestran los requerimientos de energía eléctrica necesarios para que la bomba funcione a su capacidad nominal, estos datos se dan a continuación: Frecuencia de operación Voltaje Potencia consumida 60 Hertz. 120 Volts. 0.55 Watts. Para determinar la energía consumida por el motor de la bomba en condiciones normales de operación para las prácticas en el laboratorio de mecánica se deben de utilizar los siguientes aparatos de medición: Voltímetro y Amperímetro. Después de hacer las mediciones se obtuvieron los siguientes resultados: Voltaje Intensidad de corriente 124.5 Volts 5 Amperes La frecuencia de la corriente alterna a través de las redes de transmisión y distribución en el país es de 60 Hertz, cumpliendo con la especificación de frecuencia que requiere la bomba. Ahora de la formula de potencia monofásica se tiene: Considerando un factor de potencia igual a 0.9 la potencia consumida del motor eléctrico tiene: Es muy importante conocer el consumo de energía nominal del banco de pruebas HM 150 ya que esta energía es la que proporcionara el buen funcionamiento del equipo, si fuera más bajo o más alto el rendimiento del equipo podría bajar considerablemente, a si como dañar a este. Transformación de la energía eléctrica a hidráulica a través de la bomba centrífuga. La potencia eléctrica es transmitida hacia el motor de corriente alterna, este al accionarse induce el movimiento en su rotor (flecha) el cual esta acoplado al impulsor de la bomba haciendo girar a este. El flujo de agua entra a la bomba a través del centro u ojo del impulsor y el fluido gana energía a medida que las paletas del rodete lo transportan hacia fuera en dirección radial. Esta aceleración produce un apreciable aumento de energía de presión a si como cinética. Debido a la forma de caracol de la voluta para generar un incremento gradual en el área de flujo la energía cinética a la salida del rodete se convierte en carga de presión de salida. A continuación se ilustra en un diagrama a bloques la transformación de la energía a través de una bomba para suministrársela a algún fluido: SE TRANSMITE POTENCIA AL MOTOR. P = Vicos θ MOTOR DEBIDO ALAS DIVERSAS PÉRDIDAS DEL MOTOR, ESTE ENTREGA SOLO PARTE DE LA ENERGIA ELECTRICA SUMINISTRADA, DEPENDIENDO DE LA DIFERENCIA QUE ESTE POSEA. EJE LA POTENCIA ELECTRICA ENTREGADA AL MOTOR SE TRANSFORMA EN POTENCIA MECANICA O POTENCIA DE EJE QUE MUEVE AL ROTOR DE LA BOMBA. BOMBA LA BOMBA RECIBE LA POTENCIA MECANICA DEL MOTOR Y LA TRANSMITE MEDIANTE AL IMPULSOR DEL FLUIDO. HIDRAULICA EL FLUIDO RECIBE LA POTENCIA MECANICA DE LA BOMBA EN FORMA DE POTENCIA HIDRAULICA, YA SEA MEDIANTE ELEVACION DE PRESION, POSICION O VELOCIDAD. 3.0 TEORIA BASICA DE PÉRDIDAS TRANSPORTE POR TUBERIAS EN SISTEMAS DE 3.1 MATERIALES DE TUBERÍAS Definición y conceptos previos. Se tiene que las conducciones forzadas o tuberías a presión son aquéllas que funcionan a plena sección y en las que el movimiento del líquido se debe a la presión reinante en el interior, pudiendo presentar, por tanto, pendientes y contra pendientes. Una tubería es un conjunto de tubos y accesorios unidos mediante juntas para formar una conducción cerrada. Un tubo es un elemento de sección circular. Los accesorios pueden ser: Piezas especiales: Unidades que posibilitan los empalmes, cambios de dirección (codos), derivaciones, variaciones de sección, etc. Dispositivos auxiliares: Aparatos que protegen y facilitan el buen funcionamiento de la red. Los más importantes son las válvulas y las ventosas. Las juntas son unidades que se emplean para unir tubos entre sí y con los accesorios. Una red de distribución es un conjunto de tuberías principales, secundarias, terciarias, etc. TIPOS DE VÁLVULAS. Las válvulas pueden clasificarse en función de diferentes criterios, siendo los más comunes los siguientes: Desde el punto de vista de su accionamiento: Manuales Válvulas de esfera: El dispositivo que permite la apertura y el cierre es una esfera, pudiendo adoptar posiciones intermedias para una apertura parcial. Se emplean en tuberías de pequeño diámetro. Válvulas de asiento: El elemento de cierre es un disco que se asienta sobre el cuerpo de la válvula. Válvulas de mariposa: El elemento de cierre es un disco giratorio que puede ser accionado mediante una palanca o un tornillo sinfín. Válvulas de compuerta: La válvula se cierra mediante una compuerta accionada mediante un volante. Automáticas Válvulas hidráulicas: Se accionan hidráulicamente, pudiendo ser de dos tipos: normalmente abiertas y normalmente cerradas. Electroválvulas: Se accionan de forma eléctrica, y son típicas de instalaciones automatizadas en las que el riego se programa por tiempos. Desde el punto de vista de la función que realizan: Válvulas de regulación o llave de paso. Son unidades que permiten estrangular o interrumpir el paso de una corriente líquida. Un hidrante es, en definitiva, una válvula de regulación que permite derivar agua de una tubería. Válvulas de retención: Dispositivos que consisten en una compuerta giratoria, cuya apertura se produce al paso de líquido y su cierre es por gravedad, impidiendo el retroceso. Es obligado instalar válvulas de retención en puntos estratégicos de la instalación para proteger a la red de las sobrepresiones producidas por el golpe de ariete. También a la salida del grupo motobomba, y cuando se utiliza en el riego aguas procedentes de conducciones urbanas, antes del punto de inyección de los fertilizantes, de manera que se impida el retroceso del flujo y la contaminación del agua. La válvula de pie es un caso particular de válvula de retención que se instala en la base de la tubería de aspiración para evitar su vaciado (descebado), ya que debe estar llena de agua para su funcionamiento. Válvulas de seguridad: Dispositivos que permiten la fuga automática de un caudal líquido para evitar un incremento de presión en la tubería sobre la presión prefijada. Básicamente constan de un elemento móvil sobre el que actúa, por un lado, la presión del agua, y sobre el otro, un resorte calibrado, de manera que la válvula se abre si es mayor la presión del agua, permitiendo la salida de una parte del caudal, lo que provoca una disminución de la presión. Válvula reductora de presión: Es un dispositivo que produce una pérdida de carga localizada cuando la presión sobrepasa un valor dado. Este tipo de válvulas protegen a la red de sobrepresiones y permiten una presión adecuada en las derivaciones. Válvula reguladora de caudal: Impide el paso de un caudal superior al preestablecido, manteniéndolo constante en un valor prefijado. Válvulas de drenaje: Permiten desaguar las tuberías tras el riego, con lo que se evita la formación de depósitos de precipitados y microorganismos. Básicamente constan de un resorte que se mantiene cerrado mientras existe presión en la red. Válvulas antidesagüe: Impiden el vaciado de la tubería a través de emisores situados en puntos bajos. Válvula de flotador: Corta el paso de agua cuando su nivel ha alcanzado una determinada altura. Ventosas. Son unas válvulas que permiten la salida del aire que se acumula en las conducciones de agua. La problemática de las bolsas de aire en las conducciones, la forma de evitarlas, los tipos de ventosas y su correcta colocación es motivo de otro estudio posterior. Presiones. Presión de prueba en fábrica o presión de fábrica (PF). Es aquella presión sobre la que se timbran y clasifican los tubos comerciales, que habrán de superar en fábrica sin romperse ni acusar falta de estanqueidad. Presión nominal (PN). Aquélla por la que se conoce comercialmente y que sirve para tipificar, clasificar y timbrar los tubos. Es un número convencional que coincide con la presión de trabajo a 20º C en tuberías de plástico (PVC y PE). Presión de rotura (PR). Aquélla a la cual se rompe la tubería. Presión de trabajo (PT). Máxima presión a la que se recomienda que trabaje el tubo, ya que es la máxima presión interna a la que puede estar sometido un tubo en servicio a la temperatura de utilización. Constituida por la presión de servicio más las sobrepresiones accidentales que pudieran producirse, como por ejemplo las debidas al golpe de ariete. Presión de servicio (PS): Presión a la que efectivamente se hace trabajar la tubería. Siempre debe ser menor o igual que la presión de trabajo. Se denomina coeficiente de seguridad al cociente: Consideramos una sección de tubería, que estará sometida a la presión hidráulica reinante en su interior, como representa la figura 24 Deberá existir equilibrio entre las fuerzas de tracción y el empuje estático total que actúa sobre la mitad del tubo en dirección normal al plano diametral. e: Espesor del tubo D: Diámetro del tubo T: Fuerzas resistentes de tracción que tienen a romper la tubería y que se deben a la presión hidráulica del interior. σR: Carga nominal de rotura por tracción PR : Presión de rotura Figura 24 Sección de tubería sometida a presión hidráulica Igualando ambos esfuerzos: Según la presión que pueden soportar (PR), los tubos se clasifican en: De baja presión < 3 atm De media presión 3 – 10 atm De alta presión > 10 atm 3.2 PÉRDIDAS DE CARGA POR ROZAMIENTO EN TUBERÍAS Ecuación general de Darcy-Weisbach. Suponemos una tubería por la que circula un líquido incompresible de peso específico γ, y en ella el volumen comprendido entre las secciones 1 y 2, separadas una distancia L. El elemento de tubería considerado forma un ángulo ϴ respecto a la horizontal como se muestra en la figura 25. Figura 25 Tubería de un fluido incompresible Las fuerzas que actúan sobre este volumen son: Peso de la masa del líquido (P), aplicado en el centro de gravedad (G): Fuerzas de presión (P1×S y P2×S), que sería la fuerza que ejerce el resto del líquido sobre las secciones 1 y 2, respectivamente. Fuerza de rozamiento (F), en sentido contrario al movimiento y debida al rozamiento (t) del líquido con las paredes de la tubería. La superficie lateral del cilindro considerado es un rectángulo de base L y altura c, siendo c el perímetro de la sección circular como se muestra en la figura 26. Figura 26 Superficie lateral del cilindro considerado como rectángulo Proyectando sobre el eje hidráulico las fuerzas que actúan sobre el cilindro considerado: Dividiendo por: L*Sen θ L*Sen θ = Z1 – Z2 Z1 Z2 Figra 27 Cambio de elevación y presión de un flujo a traves de de una tuberia El primer miembro de la igualdad, es la diferencia de las alturas piezométricas entre los puntos 1 y 2, es decir, la pérdida de carga que se produce en ese trayecto. Entonces, Se comprueba experimentalmente que: siendo λ un factor de proporcionalidad adimensional conocido como coeficiente de Fanning. Además, el radio hidráulico es: y como Introduciendo estos valores en [1]: En tubería cilíndrica, Por lo que Llamando modo tenemos que: , este es el coeficiente de fricción de Darcy – Weisbach. De este que es la ecuación general de Darcy - Weisbach. La pérdida de carga por unidad de longitud será: La pérdida de carga continua es directamente proporcional a la velocidad del líquido y a la longitud del tramo de tubería que estamos considerando, e inversamente proporcional a su diámetro. El factor de fricción (f) es adimensional y es función del número de Reynolds y de la rugosidad relativa de la tubería, parámetro que da idea de la magnitud de las asperezas de su superficie interior: Es un hecho demostrado que la rugosidad relativa no influye sobre f en régimen laminar (Re < 2000), ya que el rozamiento se debe fundamentalmente a la fricción de unas capas de fluido sobre otras y no de éstas sobre las paredes de la tubería. Sin embargo, para Re > 2000 las cosas cambian y la rugosidad relativa adquiere notable importancia, como veremos posteriormente. La ecuación de Darcy – Weisbach puede ponerse en función del caudal circulante, ya que el caudal que fluye por una conducción circular a plena sección está ligado al diámetro y a la velocidad media por la relación: Por lo tanto: Sustituyendo en la ecuación de Darcy – Weisbach: Operando el término constante la ecuación quedaría: Que es la ecuación de Darcy-Weisbach en función del caudal La pérdida de carga por unidad de longitud será: Se deduce que un aumento en el caudal o un aumento en la velocidad del líquido implican un aumento en la pérdida de carga, mientras que diámetro y pérdida de carga están inversamente relacionados. Rugosidad absoluta y rugosidad relativa. En el interior de los tubos comerciales existen protuberancias o irregularidades de diferentes formas y tamaños cuyo valor medio se conoce como rugosidad absoluta (K), y que puede definirse como la variación media del radio interno de la tubería. Los experimentos de Nikuradse permitieron determinar el valor de esta rugosidad absoluta. Consistieron en producir una rugosidad artificial pegando en el interior de un tubo de vidrio (liso) áridos de diferentes granulometrías tamizados, es decir, de rugosidad conocida, hasta conseguir una pérdida de carga igual que la producida en un tubo comercial de un material determinado con igual longitud y diámetro que el de vidrio. Estos tubos artificialmente preparados se conocen como tubos arenisca. Cuando una casa comercial da el valor de rugosidad K es en realidad la rugosidad media equivalente, lo que significa que se comporta del mismo modo que una tubería artificialmente preparada con la rugosidad absoluta K. Un mismo valor de rugosidad absoluta puede ser muy importante en tubos de pequeño diámetro y ser insignificante en un tubo de gran diámetro, es decir, la influencia de la rugosidad absoluta depende del tamaño del tubo. Por ello, para caracterizar un tubo por su rugosidad resulta más adecuado utilizar la rugosidad relativa (e), que se define como el cociente entre la rugosidad absoluta y el diámetro de la tubería. Diferentes expresiones de las pérdidas de carga continuas. Las pérdidas de carga por rozamiento en tuberías a presión pueden calcularse mediante dos grupos de fórmulas: 1. Fórmulas logarítmicas 2. Fórmulas empíricas Aunque en general las fórmulas logarítmicas tienen mayor precisión que las empíricas, algunas de éstas proporcionan una suficiente aproximación. En cualquier caso, es necesario conocer el tipo de flujo existente en la tubería, ya que, excepto la expresión logarítmica de White-Colebrook, cada fórmula es válida para un determinado régimen hidráulico. Por ello se debe comprobar que el número de Reynolds correspondiente a las condiciones del problema se encuentra dentro del intervalo de validez de la fórmula. Mediante las fórmulas logarítmicas, de aplicación en régimen turbulento, se calcula el coeficiente de fricción (f) para su introducción en la ecuación general de Darcy – Weisbach. Las fórmulas empíricas han sido deducidas experimentalmente para los distintos materiales y responden a la forma Es decir, Siendo 1.75<β<2. La ecuación de Hagen–Poiseuille para régimen laminar, Fue deducida experimentalmente por el ingeniero alemán Hagen y, de forma independiente, por Poiseuille, que publicaron los resultados de sus trabajos en 1939 y 1940, respectivamente. Posteriormente, en 1956, Wiedemann la dedujo de forma analítica. Velocidad de fricción y número de Reynolds de la rugosidad. Se define como velocidad de fricción a la raíz cuadrada del cociente entre el esfuerzo tangencial en las paredes de la tubería ( ) y la densidad del líquido ( ). A su vez, = = = Se denomina Nº de Reynolds de la rugosidad a la expresión adimensional: Siendo La viscosidad cinemática del líquido a la temperatura considerada y K la rugosidad absoluta de la tubería. Como Luego Y finalmente El Nº de Reynolds de la rugosidad es el producto de los tres parámetros fundamentales del flujo en tuberías a presión. Interviene en algunos ábacos para la determinación gráfica del coeficiente de fricción ( ). 3.3. EXPRESIONES DEL FACTOR DE FRICCIÓN. Recordemos que el factor de fricción o coeficiente de resistencia de Darcy-Weisbach (f) es un parámetro adimensional que depende del número de Reynolds y de la rugosidad relativa. Decíamos que la influencia de ambos parámetros sobre f es cuantitativamente distinta según las características de la corriente. En toda tubería recta que transporta un líquido a una temperatura determinada, existe una velocidad crítica (vc) por debajo de la cual el régimen es laminar. Este valor crítico que marca la transición entre los dos regímenes, el laminar y el turbulento, se corresponde con un Re = 2300, aunque en la práctica, entre 2000 y 4000 la situación es bastante imprecisa. Por lo tanto: Re < 2000: Régimen laminar. 2000 < Re < 4000: Zona crítica o de transición. Re > 4000: Régimen turbulento. Factor de fricción en régimen laminar El cálculo de f en este caso es sencillo, y se obtiene igualando la fórmula que proporciona el valor de la pérdida de carga continua para régimen laminar de Hagen-Poiseuille con la ecuación de Darcy-Weisbach: Como Entonces De modo que Y así También sabemos que Al ser Obteniendo Luego se demuestra que, en régimen laminar, el coeficiente de fricción de DarcyWeisbach es independiente de la rugosidad relativa. Sustituyendo la expresión [1] en la ecuación general de Darcy-Weisbach en función del caudal, quedaría: [2] Como Se tiene que Sustituyendo el valor de la velocidad en [2], simplificando y operando los términos constantes, se obtiene: Ecuación que indica una dependencia lineal entre el caudal y la pérdida de carga. Subcapa laminar. Para el régimen turbulento, el estudio del coeficiente de fricción es más complicado. Fue iniciado por el investigador alemán Ludwig Prandtl (1875-1953), quien expuso en 1904 su teoría de la capa límite, teoría que revolucionó la aeronáutica. Si un cuerpo se moviera en el vacío o en el seno de un fluido no viscoso (m = 0), la resistencia sería nula, por lo que el desplazamiento del cuerpo no consumiría energía. Al ser el agua y el aire fluidos poco viscosos, puede parecer que ofrecerán poca resistencia al cuerpo (por ejemplo, un avión o un submarino), pero no es así: la resistencia es grande. Prandtl descubrió que existe una capa próxima al contorno, a veces muy delgada, donde tiene lugar todo el gradiente de velocidades, ya que la velocidad debe reducirse desde su valor inicial hasta anularse en la pared. Fuera de esta capa, el líquido se comporta como no viscoso. En definitiva, la teoría de Prandtl postula que el estudio del movimiento de un líquido de pequeña viscosidad como el agua, podría asimilarse al de un líquido perfecto salvo en las proximidades de las paredes del conducto, en la cual se concentran los fenómenos de rozamiento y turbulencias y que denominó capa límite. Por lo tanto, puesto que Aun que la viscosidad ( ) sea pequeña, el término Que representa el gradiente de velocidades, es muy grande, por lo que también lo será el esfuerzo cortante (tau) en la pared. Se comprueba experimentalmente que, en contacto con las paredes de la tubería, siempre persiste una delgada capa en que la capa límite es laminar, denominada subcapa laminar o capa viscosa, ya que al ser nula la velocidad del fluido en contacto con las paredes, el Re también debe disminuir hasta el valor cero. Por tanto, al ir separándonos de la pared el régimen es laminar hasta que Re aumenta lo suficiente como para que el régimen sea turbulento. El conocimiento de la subcapa laminar es esencial para establecer el valor del coeficiente de fricción f en régimen turbulento. En definitiva, el flujo turbulento junto a un contorno sólido se puede dividir en tres zonas. Lejos del contorno, el flujo es ideal, prácticamente sin rozamientos. En las proximidades de la pared se desarrolla una zona (capa límite) sometida a esfuerzos cortantes, donde los fenómenos viscosos son importantes, ya que la velocidad sobre la pared ha de ser forzosamente nula. A pequeñísimas distancias de la pared persiste la subcapa laminar, que es una característica constante del movimiento desarrollado. Eje hidráulico Zona estelar Nucleó Central Zona de amortiguación Zona turbulencia Capa limite Subcapa laminar X(Pared) Figura 28 Perfil de velocidad para un fluido sobre una pared y sus características El espesor de la capa límite es función del Re, y puede medir desde algunas micras a varios centímetros, e incluso metros, según el caso. Comportamiento hidrodinámico de las tuberías. A) Régimen laminar. Hemos visto que Independiente de la rugosidad relativa, ya que no se forman turbulencias. Figura 29 Representación de una superficie rugosa, la cual no interviene en el factor de fricción en el flujo laminar B) Régimen turbulento. Flujo hidráulicamente liso (tubería hidráulicamente lisa). La rugosidad (K) queda cubierta por la subcapa laminar (δ). La rugosidad, por tanto, no influye en el valor de f puesto que ningún punto de la pared queda afectado por las turbulencias que producirían las rugosidades internas, comportándose la tubería como un material liso véase la figura 30. Figura 30 Representación del factor de fricción donde no influye en ningún punto de la pared Flujo hidráulicamente semi - rugoso o zona de transición. El espesor de la subcapa laminar (δ) se aproxima al valor medio de rugosidad absoluta (K), de manera que la rugosidad emerge de la subcapa laminar en unos puntos y en otros no, quedando sólo las rugosidades que emergen afectadas por la turbulencia. Es el caso más frecuente, y aquí el coeficiente de fricción depende tanto del número de Reynolds como de la rugosidad relativa como se muestra en la figura 31. Figura 31 Representación donde el coeficiente de fricción depende tanto del número de Reynolds como de la rugosidad relativa Flujo hidráulicamente rugoso (tubería hidráulicamente rugosa). Si el espesor de la capa límite (δ) es menor que la rugosidad absoluta (K), las irregularidades internas de la conducción rebasan la subcapa laminar, produciendo turbulencia completa se muestra en la figura 32. Cuanto mayor sea el número de Reynolds, más delgada será la subcapa laminar y más puntos de la pared sobresaldrán de ella. En este caso, las fuerzas de inercia son muy importantes y apenas influyen las fuerzas viscosas, por lo que el factor de fricción sólo depende de la rugosidad relativa y el número de Reynolds no tiene importancia en su determinación. Figura 32 Representación del flujo turbulento total que depende del número de Reynolds Cuantitativamente: Flujo hidráulicamente liso. Flujo hidráulicamente semi-rugoso, (zona de transición). Flujo hidráulicamente rugoso. En la práctica, se utilizan unas condiciones basadas en la proporcionalidad del número de Reynolds de la rugosidad y la relación, Ya que son más fáciles de establecer que las anteriores y se refieren a rugosidades absolutas irregulares, que es el caso real de las tuberías comerciales. Si Flujo hidráulicamente liso. Si Flujo hidráulicamente rugoso. Si K está comprendido entre los dos valores anteriores, el flujo sería hidráulicamente semi-rugoso. Experiencias de Nikuradse. Valor del coeficiente de fricción según el régimen de funcionamiento. Como es sabido, al hablar de las rugosidades absoluta y relativa, Nikuradse, discípulo de Prandtl, experimentó con tubos de rugosidad artificial conocida, creada por él mismo pegando en el interior de un tubo liso (de vidrio) arenas tamizadas, es decir, de diámetro conocido, con lo que la rugosidad artificial de estos “tubos arenisca” era conocida. Variando los caudales que circulaban por estos tubos obtuvo un diagrama en el que se relacionan los valores de K/D y Re con los hallados para f. También experimentó con tubos lisos. Los resultados de estas experiencias aparecen representados en el diagrama logarítmico típico, conocido como ábaco o diagrama de Moody. El diagrama de Moody (1944) figura 33, permite determinar el valor del factor de fricción f a partir de Re y K/D de forma directa. Es una representación log – log del factor de fricción f frente al Re, tomando como parámetro K/D. Se distinguen cuatro zonas, correspondientes a los distintos regímenes hidráulicos, correspondiendo al coeficiente de fricción f valores diferentes en en cada caso. Figura 33 diagrama de Moody 3.3.3. A. VALORES DE f SEGÚN EL RÉGIMEN DE FUNCIONAMIENTO. Re 2000, régimen laminar, por lo que Tomando logaritmos: que es la ecuación de una recta (AB) conocida como recta de Poiseuille. 2000<Re<4000, zona crítica o inestable de transición al régimen turbulento, definida por la curva BC. Re > 4000, zona de régimen turbulento liso que corresponde a la recta CD, llamada recta de Von Karman (1930), y cuya ecuación es: Aunque no aparece en forma explícita, es función del . Zona de transición del régimen turbulento, en la que Para las tuberías comerciales en esta zona se utiliza la fórmula de White-Colebrook (1938): Zona de flujo turbulento rugoso, en la que se verifica la expresión: Nikuradse, (1933) En la que f es independiente de Re, f = f(K/D). Gráficamente se observa esta independencia del número de Reynolds, ya que en esta zona las rectas son paralelas al eje Re (eje de abcisas). La región de turbulencia completa (rugosa) limita con la de transición mediante la recta FG, denominada curva de Moody, de expresión: Dividiendo por se obtiene: De manera que tenemos que: En la práctica, para (Re)r >30 se puede considerar el flujo como turbulento rugoso. Variaciones con el uso de la rugosidad absoluta. Envejecimiento de tuberías. Todos los materiales, con el paso del tiempo, disminuyen su capacidad de conducción del caudal debido a corrosiones, incrustaciones, sedimentaciones, formación de depósitos, etc. Experimentando con tuberías de fundición, Colebrook y White dedujeron que la rugosidad absoluta aumenta linealmente con el tiempo según la ecuación empírica: Siendo: K0: Rugosidad absoluta de la tubería nueva Kt: Rugosidad absoluta al cabo de t años de servicio α: Índice de aumento anual de la rugosidad Se ha demostrado que esta ecuación es también aplicable a otras clases de tuberías. Según Colebrook, en conducciones metálicas no revestidas, al cabo de 30 años el caudal se reduciría en un 30% para aguas de pH = 8, en un 45% para pH = 7 y en un 85% para pH =6. En conducciones revestidas el envejecimiento es menor, y las tuberías de hormigón liso, fibrocemento y plástico carecen de envejecimiento aparente. 3.4 FÓRMULAS EMPÍRICAS PARA EL CÁLCULO DE PÉRDIDAS DE CARGA CONTINUAS EN TUBERÍAS. Las fórmulas empíricas han sido deducidas experimentalmente para los distintos materiales y responden a la forma general Siendo c un coeficiente de proporcionalidad y 1.75<β<2. El coeficiente c no es adimensional, y por tanto, hay que utilizar las unidades adecuadas. Siempre que no se indique lo contrario, las unidades empleadas en las fórmulas corresponden al sistema internacional, es decir: En cierto modo, β es un indicador del régimen hidráulico, ya que aumenta conforme se incrementa el número de Reynolds, es decir, según el régimen es más turbulento. En riegos localizados de alta frecuencia se aconseja el empleo de fórmulas con β = 1.75, no siendo adecuadas aquéllas en que β >1.80. Es por ello que, al adoptar el coeficiente reductor de las pérdidas de carga en función del número de derivaciones de la tubería o coeficiente de Christiansen (F), se toma β =1.75 para riego por goteo mientras que b=1.80 en riegos por aspersión, como veremos en el siguiente bloque temático. En el régimen crítico, 2000<Re<4000 y Hagen-Poiseuille para régimen laminar , pero ya no es válida la relación de Ya que el flujo es inestable y se comporta unas veces como laminar y otras como turbulento. En el caso de tuberías de plástico (PVC ó PE) puede utilizarse la fórmula de Blasius para el régimen turbulento liso con bastante aproximación, ya que el error cometido no supera el 2%. Formulas para el régimen turbulento liso. En el régimen turbulento liso, y A) Blasius. Para una temperatura del agua de 20ºC, Con Q (l/h) y D (mm), la ecuación quedaría: Válida para tubos lisos y Muy indicada para tuberías de plástico en riego localizado. B) Cruciani-Margaritora . Se emplea en tuberías de polietileno (PE) y para Formulas para el régimen turbulento en la zona de transición. En este caso, A) Ecuación de Scimeni. Se emplea en tuberías de fibrocemento. La ecuación de Scimeni para la velocidad es Y como el radio hidráulico para tuberías circulares es R = D/4, quedaría: Despejando B) Ecuación de Hazen – Williams. Introduciendo este valor en la ecuación general de Darcy-Weisbach, poniendo la velocidad en función del caudal y operando, se obtiene: Ecuación válida para diámetros no inferiores a 50 mm. Los valores del coeficiente c de Hazen-Williams para los distintos materiales, clase y estado de los tubos, son los siguientes: Material, clase y estado del tubo c Tuberías de plástico nuevas 150 Tuberías muy pulidas (fibrocemento) 140 Tuberías de hierro nuevas y pulidas 130 Tuberías de hormigón armado 128 Tuberías de acero nuevas 120 Tuberías de palastro roblonado nuevas 114 Tuberías de acero usadas 110 Tuberías de fundición nuevas 100 Tuberías de palastro roblonado usadas 97 Tuberías de fundición usadas 90-80 Tabla 1 Valores del coeficiente c de Hazen- Williams C) Fórmula de Scobey. Se emplea fundamentalmente en tuberías de aluminio. En el cálculo de tuberías en riegos por aspersión hay que tener en cuenta que la fórmula incluye también las pérdidas accidentales o singulares que se producen por acoples y derivaciones propias de los ramales, es decir, proporciona las pérdidas de carga totales. Viene a mayorar las pérdidas de carga continuas en un 20%. Expresando la velocidad en función del caudal mediante la relación la ecuación quedaría: El valor del coeficiente K, que se recoge en la tabla siguiente, depende del material de la tubería. Material K Tubos de acero galvanizado con acoples 0.42 Tubos de aluminio 0.40 Tuberías de acero nuevas 0.36 Tuberías de fibrocemento y plásticos 0.32 Tabla 2 Valores del coeficiente K D) Formula de Veronesse – Datei. Se emplea en tuberías de PVC y para Formulas para el régimen turbulento rugoso. En el régimen turbulento rugoso, f = f (K/D), (Re)r > 70 y β = 2. A) Manning. Siendo n el coeficiente de rugosidad de la tubería, cuyo valor depende del tipo de material. Material n Plástico (PE) 0.006 – 0.007 Plástico (PVC) 0.007 – 0.009 Fibrocemento 0.011 – 0.012 Fundición 0.012 – 0.013 Hormigón 0.013 – 0.014 Acero comercial 0.015 Tabla 3 Coeficiente de rugosidad de la tubería n En función del material de la tubería, las fórmulas más adecuadas son: Material Fórmula PVC Veronesse – Datei PE Blasius Fibrocemento Scimeni Aluminio Scobey Fundición, Acero Hazen – Williams Tabla 4 Materiales de tubería con las formulas adecuadas Velocidades mínimas y máximas. Es necesario establecer un criterio que fije un valor máximo y otro mínimo para la velocidad del agua en las tuberías, ya que puede ser perjudicial tanto una velocidad demasiado alta como demasiado baja. Un exceso de velocidad puede: Originar golpes de ariete, cuyo valor de sobrepresión puede provocar roturas. Producir excesivas pérdidas de carga. Favorecer las corrosiones por erosión. Producir ruidos, que pueden ser muy molestos. Una velocidad demasiado baja: Propicia la formación de depósitos de las sustancias en suspensión que pudiera llevar el agua, provocando obstrucciones. Implica un diámetro de tubería excesivo, sobredimensionado, con lo que la instalación se encarece de forma innecesaria. Para presiones normales, de 2 a 5 atm, puede utilizarse la fórmula de Mougnie para establecer las velocidades límites admisibles: A partir de la fórmula de Mougnie y de la ecuación Se obtiene: Ecuación que permite calcular el diámetro mínimo de una tubería conocido el caudal aproximado que va a circular por ella. En principio, valores adecuados de la velocidad son los comprendidos entre 0.5 y 2.5 m/s. Diseño económico de tuberías. Concepto de diámetro optimo Cuando se tiene que impulsar un caudal de agua a un desnivel dado, la altura que debe generar la bomba es igual a la altura geométrica a vencer más las pérdidas de carga existentes. El primer sumando (Hg) depende exclusivamente de las cotas del terreno (desnivel entre la bomba y el depósito) y de la presión residual o mínima necesaria al final del trayecto, por lo que se trata de una energía que es independiente del diámetro. Sin embargo, para un caudal dado, el segundo sumando (h) depende exclusivamente del diámetro adoptado, de manera que como las pérdidas de carga disminuyen considerablemente al aumentar el diámetro, se precisaría menos energía para transportar el agua. Por el contrario, un aumento del diámetro da lugar a un mayor coste de la instalación. En toda instalación existe una solución que hace mínima la suma del coste de la energía necesaria para vencer las pérdidas (calculadas para un año medio) más la anualidad de amortización de la tubería. Línea de cotas piezométricas (Lp) Línea de carga estática (Lce) Figura 34 Ejemplo de un sistema de bombeo en una tubería Formulas para el dimensionado económico de tuberías. A) Formulas de Bresse Es la primera fórmula que aparece en la bibliografía hidráulica sobre el dimensionado económico de tuberías. Se trata de un criterio muy elemental y conservador, ya que corresponde a una velocidad constante de 0.57 m/s, velocidad ampliamente superada hoy en día. B) Formulas de Mendiluce. Siendo: c = coste de la tubería instalada por metro de f y por metro de longitud (pts/m.l.´ m) a = factor de amortización η = rendimiento global del grupo motor – bomba k = coeficiente de pérdida de carga en la tubería p = precio del kw×h n = número de horas de funcionamiento anual Hay más fórmulas propuestas por distintos autores, como Melzer, Vibert, etc., que tratan de determinar el diámetro óptimo para una conducción. C) Calculo basado en el evaluación real de los costos El diámetro más económico es aquél cuya suma de los gastos anuales debidos a la energía consumida más el valor de la anualidad por la inversión efectuada, es mínima. Por tanto, la ecuación a cumplir es: Gamortización + Genergía = Mínimo Esta ecuación se representa en el siguiente diagrama gasto-diámetro de la figura 34 donde el diámetro optimo para el mayor gasto posible y menor costo posible es en el punto de intersección de las curvas Gamortización y Genergía Gasto Gtotal Gamortización Genergía Dóptimo Diámetro Figura 34 Representación del diagrama de gastosdiámetro Estos cálculos requieren de programas informáticos por el volumen de datos a tener en cuenta y lo tedioso y reiterativo de su ejecución. 3.5 PÉRDIDAS DE CARGA LOCALIZADAS O ACCIDENTALES Además de las pérdidas de carga continuas o por rozamiento, vimos que en las conducciones se produce otro tipo de pérdidas debido a fenómenos de turbulencia que se originan al paso de líquidos por puntos singulares de las tuberías, como cambios de dirección, codos, juntas, derivaciones, etc, y que se conocen como pérdidas de carga accidentales, localizadas o singulares (hL, hs), que sumadas a las pérdidas de carga continuas (hC) dan las pérdidas de carga totales (hT). A) Cálculo de las pérdidas de carga localizadas. Normalmente, las pérdidas de carga continuas son más importantes que las singulares, pudiendo éstas despreciarse cuando supongan menos del 5% de las totales, y en la práctica, cuando la longitud entre singularidades sea mayor de mil veces el diámetro interior de la tubería. Salvo casos excepcionales, las pérdidas de carga localizadas sólo se pueden determinar de forma experimental, y puesto que son debidas a una disipación de energía motivada por las turbulencias, pueden expresarse en función de la altura cinética corregida mediante un coeficiente empírico K. El coeficiente K es adimensional y depende del tipo de singularidad y de la velocidad media en el interior de la tubería. En la práctica y para cálculos rápidos que no precisen de gran exactitud, se suelen adoptar los siguientes valores aproximados de K. Accesorios K L/D Válvula esférica (totalmente abierta) 10 350 Válvula en ángulo recto (totalmente abierta) 5 175 Válvula de seguridad (totalmente abierta) 2.5 - Válvula de retención (totalmente abierta) 2 135 Válvula de compuerta (totalmente abierta) 0.2 13 Válvula de compuerta (abierta ¾) 1.15 35 Válvula de compuerta (abierta ½) 5.6 160 Válvula de compuerta (abierta ¼) 24.0 900 Válvula de mariposa (totalmente abierta) - 40 “T” por la salida lateral 1.80 67 Codo a 90º de radio corto (con bridas) 0.90 32 Codo a 90º de radio normal (con bridas) 0.75 27 Codo a 90º de radio grande (con bridas) 0.60 20 Codo a 45º de radio corto (con bridas) 0.45 - Codo a 45º de radio normal (con bridas) 0.40 - Codo a 45º de radio grande (con bridas) 0.35 - Tabla 5 Accesorios para cálculos en la práctica que no precisen gran exactitud En conducciones circulares, la fórmula [1] puede expresarse en función del gasto mediante la ecuación: Siendo El valor de m para distintos diámetros comerciales es el siguiente: D (metros) m’ D (metros) m’ 0.05 13222 0.25 21155 0.06 6376.4 0.30 10202 0.07 3441.8 0.35 5506.7 0.08 2017.5 0.40 3228.1 0.09 1259.5 0.45 2015.3 0.10 826.38 0.50 1322.2 0.15 163.24 0.60 637.64 0.20 51.649 0.70 344.18 Tabla 6 Valor de m, para distintos diámetros comerciales B) Longitud equivalente de la conducción. Un método no completamente exacto pero válido a efectos de estimar las pérdidas de carga localizadas consiste en expresarlas en forma de longitud equivalente (Le), es decir, valorar cuántos metros de tubería recta del mismo diámetro producen una pérdida de carga continua que equivale a la pérdida que se produce en el punto singular. Por tanto, la longitud equivalente de una singularidad puede determinarse igualando las fórmulas para el cálculo de hs y hc: Y si entonces: La pérdida de carga total en una tubería de longitud L con i singularidades de longitud equivalente Lei cada una de ellas, será la que produce una tubería del mismo diámetro pero con una longitud total Por ejemplo, si la suma de los coeficientes de resistencia (K) en las singularidades de una tubería de 200 mm de diámetro y f=0.020 es K=15, significa que para calcular las pérdidas de carga totales, la longitud real de la conducción deberá aumentarse en una longitud equivalente de Le=150 m, es decir, 750 diámetros. Esta longitud equivalente origina la misma pérdida de carga que los puntos singulares a los que sustituye. Si la pérdida de carga por rozamiento se expresa mediante la ecuación de Darcy simplificada: Es decir, se considera Entonces, la longitud equivalente de la conducción puede calcularse igualando las fórmulas [2] y [3]: Luego A efectos prácticos, en muchos casos se simplifica el cálculo suponiendo que las hs suponen un porcentaje del orden del 5 – 20 % de las pérdidas de carga continuas, según el número y tipo de singularidades. Si x es el porcentaje que supone Luego respecto de : En estos casos, por tanto, la pérdida de carga total será la producida en una tubería por rozamiento incrementando su longitud entre un 5–20%. Pérdidas de carga localizadas de mayor importancia cuantitativa. A) Pérdidas localizadas en un ensanchamiento brusco de sección Aunque la tubería se ensanche bruscamente, el flujo lo hace de forma gradual, de manera que se forman torbellinos entre la vena líquida y la pared de la tubería, que son la causa de las pérdidas de carga localizadas. Región turbulenta D1 D2 Figura 35 Pérdidas de carga localizadas de mayor importancia cuantitativa. Aunque en la mayoría de los casos las pérdidas de cargas localizadas se calculan a partir de la ecuación [1], obteniéndose K empíricamente, en este caso pueden deducirse de forma analítica. Para ello suponemos que y Aplicando Bernoulli entre 1 y 2, se obtiene: Ya que Y Entonces Como Entonces Caso particular: Tubería que abastece un depósito Figura 36 Tubería que abastece un depósito En este caso, la superficie S2 es mucho mayor que la S1, por lo que la relación entre ambas tenderá a cero. Por lo tanto, en este caso K=1, y la pérdida de carga en la desembocadura será: Es decir, se pierde toda la energía cinética en la entrada al depósito. B) Pérdidas localizadas en un ensanchamiento gradual de sección Son los difusores, en los que se producen, además de las pérdidas de carga por rozamiento como en cualquier tramo de tubería, otras singulares debido a los torbellinos que se forman por las diferencias de presión (al aumentar la sección disminuye la velocidad, y por lo tanto el término cinético, por lo que la presión debe aumentar). Zona de separación para un ángulo grande de cono Ángulo de cono Figura 37 Pérdidas localizadas en un ensanchamiento gradual de sección A menor ángulo de conicidad (q), menor pérdida de carga localizada, pero a cambio se precisa una mayor longitud de difusor, por lo que aumentan las pérdidas de carga continuas. Se trata de hallar el valor de q para el que la pérdida de carga total producida sea mínima. Gibson (Torres Sotelo, 1996) demuestra experimentalmente que el ángulo óptimo de conicidad es de unos 6º, y proporciona la siguiente fórmula empírica para calcular las pérdidas de carga totales: Los valores de lamda, también según Gibson, son los siguientes: q 6º 10º 15º 20º 30º 40º 50º 60º lamda 0.14 0.20 0.30 0.40 0.70 0.90 1.00 1.10 Tabla 7 Valores de Lamda según Gibson C) Pérdidas localizadas en un estrechamiento brusco de sección. Vena contracta Flujo Zonas de turbulencia 1 2 Figura 38 Pérdidas localizadas en un estrechamiento brusco de sección En este caso, el flujo continúa convergiendo después de la embocadura durante una cierta distancia, a partir de la cual se produce su ensanchamiento. Por tanto, se formarán turbulencias entre el flujo y las paredes de la tubería, y también entre éstas y la vena líquida contraída, como se indica en la figura. Los valores de K se obtienen de forma suficientemente aproximada en función de la relación entre los dos diámetros: D1/D2 1.2 1.4 1.6 1.8 2.0 2.5 3.0 4.0 5.0 K 0.08 0.17 0.26 0.34 0.37 0.41 0.43 0.45 0.46 Tabla 8 Obtención de los valores de K en función de los diámetros Caso particular: Tubería a la salida de un depósito (embocadura) En este caso, la pérdida de carga depende del tipo de conexión entre la tubería y el depósito observe la figura 39. Figura 39 (a) Figura 39 (b) Figura 39(c) (1) Embocadura de arista viva: K»0.5 (2) Embocadura tipo entrante: K»1.0 (3) Embocadura abocinada: K»0.01-0.08, según el grado de abocina miento. Se puede considerar un valor medio de K»0.5. D) Pérdidas localizadas en un estrechamiento gradual de sección (Tobera) Puesto que el líquido aumenta su velocidad al pasar por la tobera, también disminuye su presión. Por tanto, las condiciones no favorecen la formación de torbellinos, siendo casi la totalidad de las pérdidas de carga que se producen debidas al rozamiento. Los valores de K suelen oscilar entre 0.02 y 0.04, por lo que, en la práctica, estas pérdidas de carga se desprecian. E) Otras pérdidas localizadas de interés Son importantes por lo extendido del uso de estas piezas especiales las pérdidas de carga producidas en válvulas, codos de distintos ángulos y ramificaciones en “T” (pérdidas por bifurcación o empalme del flujo, ver figura 40). Bifurcación Figura 40 (a) Empalme Figura 40 (b) Consideraciones prácticas para evaluar las pérdidas de carga accidentales. A) Para válvulas, puede tomarse como equivalente la pérdida de carga por rozamiento en una tubería recta de 10 m de longitud y de igual diámetro que el accesorio. B) En ocasiones, puede tomarse una longitud total de tubería incrementada en un 5 – 20 %, dependiendo de la longitud y el mayor o menor número de puntos singulares. C) Las pérdidas localizadas en general pueden despreciarse cuando, por término medio, haya una distancia de 1000 metros entre dos puntos singulares. PRÁCTICAS DE LABORATORIO PARA PÉRDIDAS EN TUBERÍAS Y ACCESORIOS HM-150.11 4.1 OPERACIÓN DEL BANCO BÁSICO DE HIDRÁULICA PARA PÉRDIDAS EN TUBERÍAS HM -150.11. 4.2 DETERMINACIÓN DE PÉRDIDAS DE ENERGIA A TRAVES DE UNA VALVULA DE COMPUERTA 4.3 DETERMINACION DE PÉRDIDAS A TRAVES DE UNA VALVULA DE AGUJA 4.4 MEDICIÓN DE CORRIENTE VOLUMÉTRICA CON TUBO VENTURI PRACTICA DE LABORATORIO No 1 4.1OPERACIÓN DEL BANCO BÁSICO DE HIDRÁULICA PARA PÉRDIDAS TUBERÍAS HM 150.11 OBJETIVOS El trayecto de medición desplazable sirve como alojamiento para los diferentes objetos de medición. El suministro de Estudiar las partes que conforman al modelo de hidráulica HM básico HM 150 de técnica de corrientes o a través de la red del laboratorio. Con el 150.11. Conocer los accesorios disponibles del modelo HM150.11 para agua tiene lugar mediante el módulo poderlos HM 150 puede establecerse un circuito cerrado de agua. operar correctamente. EQUIPO Poner en funcionamiento el banco básico de hidráulica para los diferentes tipos de prácticas. Gunt, Hamburgo. D22881. Equipo para la enseñanza técnica "dinámica de fluidos aplicada” Banco básico de hidráulica HM EXPOSICION El equipo HM 150.11 permite realizar 150.11 para perdidas en tuberías. experimentos para la medición de caudal Banco básico de hidráulica modelo HM y de presión y cálculos de pérdidas de 150 corriente y transcursos de presión en tubos y elementos de tubería especiales. Set de pruebas para perdidas en tuberías y accesorios del modelo HM 150.11 El equipo está compuesto de un bastidor de tubo de acero cuadrado con una PROCEDIMIENTOS pared posterior recubierta de polvo, en la pared posterior manómetros de se han nivel fijado con dos tuercas moleteadas en cruz, los manómetros pueden montarse en dos posiciones en la pared posterior. Advertencias: En esta práctica de laboratorio se maneja equipo de mucho cuidado No poner en funcionamiento la bomba centrífuga sin agua, asegurarse de que no tenga fugas de agua el equipo en 9.- Ajustando al mismo tiempo la válvula cada unión de las tuberías. de purga y la válvula de desagüe en el 1.- Pasos para la práctica de laboratorio. manómetro, debe regularse el nivel del agua de tal modo que ambas columnas 2.- Colocar la construcción de ensayo en de agua se encuentren dentro del rango el módulo básico HM 150 de técnica de de medición. corrientes con la evacuación encima del depósito volumétrico. 3.- Soltar las tuercas moleteadas en cruz de la parte traseras de las fijaciones de CONEXIÓN DE MANÓMETRO Y MANEJO manómetros y colocar el manómetro en Conectar el manómetro a los agujero más abajo, volver a apretar las puntos de medición deseados tuercas moleteadas en cruz. mediante las mangueras con 4.- Establecer la unión de mangueras los entre HM 150 y el equipo. autoblocantes. 5.- Abrir el desagüe hm 150. 6.- Conectar la bomba y abrir lentamente el grifo principal de HM 150.11. 7.-Conectar el manómetro a los puntos de medición deseados. Abrir trayecto de medición deseados y purgar el manómetro, manómetro doble. el grifo rápidos esférico del desagüe. Conectar la bomba en HM 150. Cerrar la válvula de purga superior. Abrir 8.- Abrir lentamente el grifo esférico del acoplamientos ambas válvulas de desagüe inferiores. Abrir lentamente el grifo esférico en la afluencia del trayecto de tubo a medir. PRUEBA DE CONOCIMIENTOS 5________________________________ ________________________________ 10.- De acuerdo con las imágenes 1 y 2, 6________________________________ mencione ________________________________ cada una de sus partes y accesorios del modelo de Hidráulica HM 150.11 7________________________________ ________________________________ Modelo HM 150 8________________________________ ________________________________ 9________________________________ ________________________________ Modelo HM 150.11 Figura 1. 1________________________________ ________________________________ 2________________________________ ________________________________ 3________________________________ ________________________________ 4________________________________ ________________________________ Figura 2 1 a 6 1________________________________ 5________________________________ ________________________________ ________________________________ 2________________________________ 6________________________________ ________________________________ ________________________________ 3________________________________ 7________________________________ ________________________________ ________________________________ 4________________________________ 8________________________________ _________________________________ _________________________________ 9___________________________________ ___________________________________ 10__________________________________ __________________________________ De acuerdo con la teoría que escala tiene el manómetro doble y qué tipo de presiones se pueden medir con el mismo ____________________________________ ____________________________________ ____________________________________ De acuerdo con la práctica de laboratorio explique cómo se ponen al mismo nivel las válvulas de purga y de desagüe ____________________________________ ____________________________________ Qué tipo de presiones se miden con la válvula de purga abierta y con la válvula de purga cerrada ____________________________________ ____________________________________ _________________________________ PRACTICA DE LABORATORIO No 2 4.2 DETERMINACION DE PÉRDIDAS DE ENERGIA A TRAVES DE UNA VALVULA DE COMPUERTA OBJETIVOS Examinar el PROCEDIMIENTOS comportamiento del Advertencias: En esta práctica de fluido a través de la estrangulación de laboratorio se maneja equipo de mucho la válvula de compuerta. cuidado Medir el flujo volumétrico en la válvula No poner en funcionamiento la bomba de centrífuga sin agua, asegurarse de que compuerta de acuerdo a la posición de apertura de esta no tenga fugas de agua el equipo en Medir las pérdidas de energía en la cada unión de las tuberías válvula de compuerta de acuerdo a la posición de apertura de esta 1. a) Cierre todas las válvulas EXPOSICION en todos los trayectos del es modulo HM 150.11 y solo el deje abierto el trayecto de levantamiento de una compuerta o medición 6 para realizar las cuchilla (la cuál puede ser redonda o pruebas con la válvula de rectangular) y así permitir el paso del compuerta. La válvula una válvula que de compuerta abre mediante fluido. Lo que distingue a una válvula de compuerta es el sello, el cual se hace mediante el asiento del disco en dos b) Coloque la válvula de compuerta en el trayecto de medición 6 áreas distribuidas en los contornos de ambas caras del disco. Las caras del disco pueden ser paralelas o en forma de cuña. Las válvulas de c) Verifique que la válvula de compuerta este cerrada por completo compuerta no son empleadas para regulación. d) Encienda la bomba del modelo HM 150 alimentar el trayecto 6. para 2 a) Observe y diga si existe flujo a la salida del trayecto y mídalo ______________________________ ______________________________ b) Abra la válvula de aguja a 1 3 a) Conecte los manómetros a la entrada y salida de las válvulas de aguja. b) Abra la válvula de aguja a 1 revoluciones y encienda la bomba y tome las lecturas de los manómetros a la entrada y salida de la válvula revoluciones; Observe y diga si hay _________________ flujo de agua y mida. Exprese el resultado en ______________________________ ______________________________ c) Mediante la ecuación de la energía calcule las pérdidas que se presentan en la entrada y salida de la válvula c) siguiendo el mismo procedimiento de los datos anteriores llene la siguiente tabla _________________________________ REVOLUCIONE S d) Siguiendo el procedimiento del punto anterior, calcule las pérdidas para las diferentes posiciones de abertura de la válvula de aguja CORRIENTE VOLUMETRIC AQ _________________________________ REVOLUCIONES 0 1 2 3 4 5 10 15 0 1 2 3 4 5 10 15 d) Apague la bomba y cierre la válvula de aguja PERDIDAS PRUEBA DE CONOCIMIENTO 1.- Mencione algunas características de la válvula de compuerta. ______________________________ ______________________________ ______________________________ 2.-Mencione algunas características que tiene la válvula de compuerta. 5.- Con los valores de medición anotados en el inciso 2(c) dibuje una grafica 40 30 20 10 0 1 2 4 5 10 15 Válvula 3.- En la practica en donde se aplica la válvula de compuerta y porque. ______________________________ ______________________________ _____________________________ 3 Revoluciones 6.- Con los valores de medición anotados en el inciso 3 d) dibuje una grafica. 40 4.- Mencione algunas desventajas de las válvulas de compuerta ______________________________ ______________________________ _____________________________ 30 20 10 0 1 2 3 4 5 Válvula Revoluciones 10 15 PRACTICA DE LABORATORIO No 3 4.3 DETERMINACION DE PERDIDAS DE ENERGIA A TRAVES DE UNA VALVULA DE AGUJA OBJETIVOS Examinar el comportamiento del fluido a través de la estrangulación de la válvula de aguja. Medir el flujo volumétrico en la válvula de flujo de acuerdo a la posición de apertura de esta. Medir las pérdidas de energía en la válvula de aguja de acuerdo a la posición de apertura de esta. Es posible encontrar diseños con la disposición de los puertos de entrada y salida de la válvula de forma angular, recta (90º) o lineal (0º). En centrales hidráulicas se utilizan las válvulas de aguja como bypass a la válvula de mariposa o esférica de entrada a las turbinas. Primero se opera con la válvula de aguja, que puede trabajar mejor que la principal a grandes diferencias de presión sin cavitación, y una vez que la válvula principal está a presiones equilibradas se realiza su obertura evitando un golpe de ariete de la instalación. PROCEDIMIENTOS EXPOSICION Advertencias: La válvula de aguja es llamada así por el vástago cónico que hace de obturador sobre un orificio de pequeño diámetro en relación el diámetro nominal de la válvula. En esta práctica de laboratorio se maneja equipo de mucho cuidado No poner en funcionamiento la bomba centrífuga sin agua, asegurarse de que El desplazamiento del vástago, si es de rosca fina, es lento y el hecho de que hasta que no se gira un buen número de vueltas la sección de paso del fluido es mínima, convierte esta válvula en una buena reguladora de caudal, por su estabilidad, precisión y el diseño del obturador que facilita un buen sellado metálico, con poco desgate que evita la cavitación a grandes presiones diferenciales. no tenga fugas de agua el equipo en cada unión de las tuberías 1. a) Cierre todas las válvulas en todos los trayectos del modulo HM 150.11 y solo deje abierto el trayecto de medición 6 para realizar las pruebas con la válvula de compuerta. b) Coloque la válvula de compuerta en el trayecto de medición 6 c) Verifique que la válvula de compuerta este cerrada por completo REVOLUCIONE S CORRIENTE VOLUMETRIC AQ 0 1 d) Encienda la bomba del modulo HM 150 para alimentar el trayecto 6. 2 3 2 a) Observe y diga si existe flujo a la salida del trayecto y mídalo _________________________________ _________________________________ _________________________________ _________________________________ ________________________________ b) Abra la válvula de aguja a 1 revoluciones; Observe y diga si hay flujo de agua y mida. Exprese el resultado 4 5 10 15 d) Apague la válvula y cierre la válvula de aguja en ______________________________ ______________________________ ______________________________ _____________________________ 3 a) Conecte los manómetros a la entrada y salida de las válvulas de aguja. c) siguiendo el mismo procedimiento de los datos anteriores llene la siguiente tabla b) Abra la válvula de aguja a 1 revoluciones y encienda la bomba y tome las lecturas de los manómetros a la entrada y salida de la válvula _________________ c) Mediante la ecuación de la energía calcule las pérdidas que se presentan en la entrada y salida de la válvula _________________________________ _________________________________ _________________________________ _________________________________ __________________ REVOLUCIONES d) Siguiendo el procedimiento del punto anterior, calcule las pérdidas para las diferentes posiciones de abertura de la válvula de aguja 3 0 1 2 4 5 10 15 PERDIDAS PRUEBA DE CONOCIMIENTO 1.- Mencione algunas características que tiene la válvula de aguja. ______________________________ ______________________________ 4.- Con los valores de medición anotados en el inciso 2(c) dibuje una grafica 40 30 20 10 0 2.- En la práctica ¿En donde se utiliza la válvula de aguja y porque? ______________________________ ______________________________ _____________________________ 3.- Qué diferencia hay entre la válvula de compuerta y la válvula de aguja. ______________________________ ______________________________ ______________________________ 1 2 3 4 5 10 15 Revoluciones Válvula 5.- Con los valores de medición anotados en el inciso 3 (d) dibuje una grafica. 40 30 20 10 0 1 2 3 4 5 Válvula Revoluciones 10 15 PRACTICA DE LABORATORIO No 4 4.4 MEDICIÓN DE CORRIENTE VOLUMÉTRICA CON TUBO VENTURI. h OBJETIVOS cónicas unidas por un tubo estrecho Aprender a instalar el tubo Venturi en el en el que el fluido se desplaza consecuentemente banco básico de hidráulica HM 150.11 a mayor velocidad. La presión en el tubo Como se puede efectuar una medición de corriente volumétrica con el tubo Venturi. Venturi puede medirse por un tubo vertical en forma de U conectando la región ancha y la canalización estrecha. La diferencia de alturas del líquido en el tubo en U permite medir EXPOSICION la presión en ambos puntos y consecuentemente la velocidad. Un tubo Venturi es un dispositivo inicialmente diseñado para medir la velocidad de un fluido aprovechando el efecto Venturi; Este dispositivo es aplicado a la industria en la cual se transportan fluidos y es necesario conocer el caudal y/o la velocidad de este a través de la tubería.Sin embargo, algunos se utilizan para acelerar la velocidad de un fluido obligándole a atravesar un tubo estrecho en forma de cono. Estos modelos se utilizan en numerosos dispositivos en los que la velocidad de un fluido es importante. La aplicación clásica de medida de velocidad de un fluido consiste en un tubo formado por dos secciones IMAGEN DE TUBO VENTURI CON PÉRDIDAS PRÁCTICA SIMULADAS EN LA PROCEDIMIENTOS b) Ajuste la corriente volumétrica mediante el grifo esférico del trayecto de medición. 1. a) Montar el tubo Venturi en el trayecto de medición 6 el cual se encuentra en el modulo HM 150.11. 3. a) Conecte los manómetros a las tomas de presión del tubo Venturi y anote estas medidas. b) Tener en cuenta el sentido del flujo del agua en el tubo Venturi; la entrada de este es la sección cónica convergente Entrada__________ que termina con el diámetro igual a la de Garganta_________ la garganta. b) De las especificaciones del equipo el c) Asegurarse que todas las válvulas en diámetro de la entrada del tubo Venturi todos los trayectos excepto en donde se es D= 28.4 mm y el de la garganta es d= encuentra el tubo Venturi estén cerradas. 14.0 mm. Determine el área de la garganta. _________________________________ d) Durante el montaje del objeto de medición debe prestarse atención a que _________________________________ ________________________ los anillos de obturación se encuentran debidamente en la ranura. c) Determine la temperatura del agua que se encuentra dentro del depósito e) Apretar las tuercas de unión sólo con mediante un termómetro fuerza manual. _________________________________ __________________ 2. a) Encienda la bomba del modulo HM 150 para hacer fluir el agua a través del d) De la temperatura obtenida busque en trayecto de medición 6. la siguiente tabla el valor de la densidad del agua. 121 tubo Venturi utilizado tiene un índice de . caudal Entonces la corriente volumétrica con los datos obtenidos Temperatura Densidad (°C) ( 5 1000 10 1000 15 1000 puede calcularse mediante la fórmula: ) De la formula anterior calcule el flujo volumétrico 20 998 25 997 obtenidos a partir de los datos anteriormente _________________________________ _________________________________ 30 996 35 994 40 992 45 990 50 988 _________________________________ _______________________________ e) Anote el valor encontrado de la densidad ________________________________ f) Como el fluido es agua y es un fluido incompresible el índice de expansión es y de acuerdo a la DIN 1952 el 122 PRUEBA DE CONOCIMIENTO _________________________________ _________________________________ 1.- ¿Que es un tubo Venturi y para qué sirve? _________________________________ _________________________________ _________________________________ _________________________________ 6.- Como podemos calcular la corriente volumétrica y con que formula. 2.- Mencione algunas características del tubo Venturi. _________________________________ _________________________________ _________________________________ ________________________________ _________________________________ _________________________________ ________________________________ 3.- Como puede medirse la presión en el tubo Venturi. 7.- De acuerdo con la práctica ¿qué se requiere para calcular el índice de caudal? _________________________________ _________________________________ _________________________________ _________________________________ _________________________________ _________________________________ _________________________________ 4.- Que tipo de medidas se pueden obtener el tubo Venturi. _________________________________ _________________________________ _________________________________ ________________________________ 5.- Donde podemos encontrar la cavitación en el tubo Venturi. 123 COSTOS El banco básico de hidráulica modelo HM 150, así como el set de pruebas para pérdidas en tuberías y accesorios, modelo HM 150.11 fueron adquiridos mediante el proyecto PIFI en el año 2006 y 2008 respectivamente Los costos de ambos equipos fueron adquiridos al proveedor de DEDUTEL de S.A de C.V. -Banco Básico de Hidráulica modelo HM 150; $232 558.38 pesos - Set de Pruebas para Pérdidas en Tuberías y Accesorios, modelo HM 150.11: $370 445.13 pesos CAPITULO III 125 APORTACIONES O CONTRIBUCIONES AL DESARROLLO Con la aplicación de los conocimientos adquiridos en la parte teórica mas los conocimientos obtenidos en la práctica, el estudiante será capaz de comprender, analizar y diseñar un sistema de tuberías en serie y/o paralelo con sus distintos accesorios como por ejemplo; diferentes tipos de válvulas, codos, uniones de tuberías etcétera, dependiendo de la aplicación. Dichos conocimientos están orientados a lograr que los procesos de funcionamiento en la industria sean cada vez mas óptimos en cuanto a ahorro de energía, costos y de producción. Con estos conocimientos se contribuye al desarrollo de la pequeña, mediana y grande industria donde exista el uso de fluidos a través de tuberías para los diferentes procesos, pero sobre todo contribuye a la formación académica de los estudiantes al llevar a cabo la realización de las prácticas de laboratorio reforzando los conocimientos teóricos adquiridos en clase haciendo que la formación del estudiante de ingeniería mecánica eléctrica sea más completa 126 BIBLIOGRAFIA LIBROS Introducción a la mecánica de fluidos Carlos Arturo Duarte Agudelo José Roberto Niño Vicentes Universidad Nacional de Colombia Mecánica de Fluidos Potteer, M.C ; D.C Wiggertm, D.C... Ed: Paraninfo Mecánica de Fluidos 9a Ed Viguer . J.M. McGraw-Hill/interamericana de de España, S.A.U Neumática, Hidráulica y Electricidad Aplicada José Roldán Viloria Thomson Referencias electrónicas http://www.univideo.es/Areas/Mecanica.Fluidos/docencia/_asignaturas/mec anica_de_fluidos/07_08/MF07_perididasdecarga.pdf http://www.scribd.com/doc/8331609/Mecanica-de-Fluidos-Execelente-Libro http://www.librosgratis.org/stag/mecanica-de-fluidos.com http://www.lawebdefisica.com/dicc/bernulli http://www.gunt.de/static/s4569_3.php 127 APENDICE SIMBOLO DIMENSIONES DESCRIPCIÓN A L² Área °C θ Temperatura, Celsius Cp .... Coeficiente de presión CQ …. Coeficiente de descarga CV …. Coeficiente de velocidad D L Diámetro E ML²/T² Energía °F θ Temperatura, Fahrenheit g L/T² Aceleración debida a la gravedad hƒ L Pérdida de carga por fricción de tubería hp L Carga suministrada por bomba J ML²/T² Joule, unidad de trabajo K …. Coeficiente del flujo k θ Temperatura, kelvin KS L Tamaño equivalente de rugosidad de área 128 N ML/T² Newton, unidad de fuerza NS L¾/T3/2 Velocidad especifica n T-1 Frecuencia hertz P ML²/T³ Potencia p M/LT² Presión Pt M/LT² Presión total Q M/LT² Descarga, flujo volumétrico Rh L Radio hidráulico Re …. Numero de Reynolds S …. Gravedad específica s T Segundos, segundos Tt θ Temperatura total t T Tiempo V L/T Velocidad V L³ Volumen W ML²/T² Trabajo W ML²/T³ Watt, unidad de potencia к …. Constante de turbulencia 129 μ M/LT Viscosidad, dinámica ρ M/L³ Densidad ρt M/L³ Densidad 130