Práctica 2. Estadística Descriptiva

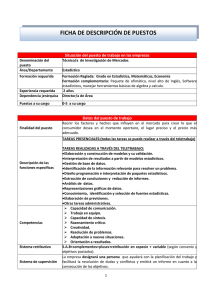
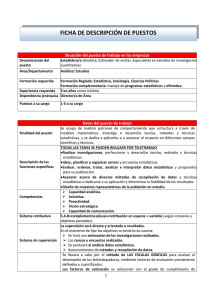
Práctica 2. Estadística Descriptiva
Ejercicio 1
Mucha gente manifiesta reacciones de alergia sistémica a las picaduras de
insectos. Estas reacciones varían de paciente a paciente, no sólo en cuanto a
gravedad, sino también en el tiempo transcurrido hasta que se inicia la
reacción. Los datos siguientes representan este “tiempo hasta el inicio de la
reacción” en 40 pacientes que experimentaron una reacción sistémica a la
picadura de abeja:
10.5
11.6
12.5
7.4
11.2
6.2
11.2
8.6
9.9
7.9
9.1
13.6
15.0
8.3
10.4
14.7
11.4
10.9
9.1
11.5
12.7
8.1
13.4
11.5
16.5
3.8
12.3
10.9
10.1
10.5
5.9
9.8
12.7
11.7
11.4
12.9
11.4
8.4
8.8
9.9
a) Introducir los datos.
b) Determinar:
i.
Número de datos
ii.
Valores máximo y mínimo
iii.
Tabla de frecuencias
iv.
Representaciones gráficas
v.
Interpretación
El cálculo de la tabla de frecuencias se hace a partir del menú Analizar… Estadísticos
Descriptivos
La generación de la tabla de frecuencias se obtiene marcando la casilla de verificación
Mostrar tablas de frecuencias. Esta opción permite también la determinación de
algunos estadísticos, para ello basta con pulsar en el botón Estadísticos, así como una
serie de gráficos, pulsando en el botón Gráficos
Como podemos observar con esta opción, SPSS nos proporciona todos los estadísticos
descriptivos elementales.
Los gráficos que permite son:
Seleccionados los estadísticos pedidos en la práctica, así como el cálculo de la tabla de
frecuencias y el gráfico de barras, los resultados obtenidos son los siguientes:
Frecuencias
Estadísticos
TIEMPO
N
Válidos
Perdidos
40
0
Mínimo
3.8
Máximo
16.5
Se han analizado 40 datos en los que no hay información faltante
TIEMPO
Válidos
3.8
5.9
6.2
7.4
7.9
8.1
8.3
8.4
8.6
8.8
9.1
9.8
9.9
10.1
10.4
10.5
10.9
11.2
11.4
11.5
11.6
11.7
12.3
12.5
12.7
12.9
13.4
13.6
14.7
15.0
16.5
Total
Frecuencia
1
1
1
1
1
1
1
1
1
1
2
1
2
1
1
2
2
2
3
2
1
1
1
1
2
1
1
1
1
1
1
40
Porcentaje
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
5.0
2.5
5.0
2.5
2.5
5.0
5.0
5.0
7.5
5.0
2.5
2.5
2.5
2.5
5.0
2.5
2.5
2.5
2.5
2.5
2.5
100.0
Porcentaje
válido
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
2.5
5.0
2.5
5.0
2.5
2.5
5.0
5.0
5.0
7.5
5.0
2.5
2.5
2.5
2.5
5.0
2.5
2.5
2.5
2.5
2.5
2.5
100.0
Porcentaje
acumulado
2.5
5.0
7.5
10.0
12.5
15.0
17.5
20.0
22.5
25.0
30.0
32.5
37.5
40.0
42.5
47.5
52.5
57.5
65.0
70.0
72.5
75.0
77.5
80.0
85.0
87.5
90.0
92.5
95.0
97.5
100.0
En la tabla de frecuencias nos aparece la frecuencia de repetición de cada dato así como
los porcentajes acumulados (equivalentes a las frecuencias relativas).
Histograma:
TIEMPO
10
8
6
Frecuencia
4
2
Desv. típ. = 2.53
Media = 10.6
N = 40.00
0
4.0
6.0
5.0
8.0
7.0
10.0
9.0
12.0
11.0
14.0
13.0
16.0
15.0
17.0
TIEMPO
También es posible obtener este gráfico a partir del menú principal Gráficos…
Histograma; los resultados son los mismos. Sin embargo, tanto en uno como en otro
caso, con esta opción SPSS construye el histograma directamente, sin que podamos
modificar ni la amplitud ni el número de intervalos. Este inconveniente se puede
solventar con la utilización de lo que SPSS denomina Gráficos Interactivos.
Ejercicio 2:
Una variable de interés en el estudio del cangrejo Xanthidae (pequeño
cangrejo que habita en las proximidades de Gloucester Point, Virginia) es el
“número de huevos puestos por individuo”. La siguiente tabla muestra las
observaciones obtenidas para 37 cangrejos:
1959
2462
4801
10241
4000
4534
3378
737
962
7020
7343
5321
3894
6725
4189
849
1801
6964
8973
5749
5099
7428
4327
6837
8372
9359
2412
8639
8255
a) Introducir los datos.
b) Determinar:
i. Número de datos
ii. Valores máximo y mínimo
iii. Tabla de frecuencias
iv. Representaciones gráficas
v. Interpretación
N
Estadísticos
NHUEVOS
Válidos
Perdidos
37
0
Mínimo
737
Máximo
12130
9166
7624
7417
6142
2802
1548
6082
12130
NHUEVOS
Válidos
737
Frecuencia
1
Porcentaje
2.7
Porcentaje
válido
2.7
Porcentaje
acumulado
2.7
849
1
2.7
2.7
5.4
962
1
2.7
2.7
8.1
1548
1
2.7
2.7
10.8
1801
1
2.7
2.7
13.5
1959
1
2.7
2.7
16.2
2412
1
2.7
2.7
18.9
2462
1
2.7
2.7
21.6
2802
1
2.7
2.7
24.3
3378
1
2.7
2.7
27.0
3894
1
2.7
2.7
29.7
4000
1
2.7
2.7
32.4
4189
1
2.7
2.7
35.1
4327
1
2.7
2.7
37.8
4534
1
2.7
2.7
40.5
4801
1
2.7
2.7
43.2
5099
1
2.7
2.7
45.9
5321
1
2.7
2.7
48.6
5749
1
2.7
2.7
51.4
6082
1
2.7
2.7
54.1
6142
1
2.7
2.7
56.8
6725
1
2.7
2.7
59.5
6837
1
2.7
2.7
62.2
6964
1
2.7
2.7
64.9
7020
1
2.7
2.7
67.6
7343
1
2.7
2.7
70.3
7417
1
2.7
2.7
73.0
7428
1
2.7
2.7
75.7
7624
1
2.7
2.7
78.4
8255
1
2.7
2.7
81.1
8372
1
2.7
2.7
83.8
8639
1
2.7
2.7
86.5
8973
1
2.7
2.7
89.2
9166
1
2.7
2.7
91.9
9359
1
2.7
2.7
94.6
10241
1
2.7
2.7
97.3
100.0
12130
1
2.7
2.7
Total
37
100.0
100.0
ê
ê
ê
8
ê
ê
ê
ê
ê
Recuento
6
ê
ê
ê
ê
ê
4
ê
ê
ê
ê
ê
2
ê
ê
ê
ê
ê
ê
ê
ê
ê
2500
ê
ê
ê
ê
ê
ê
5000
ê
ê
ê
ê
7500
nhue vos
ê
ê
ê
ê
ê
ê
10000
ê
ê
ê
Ejercicio 3:
Actualmente se realizan esfuerzos para elaborar fibras textiles de fibra de
turba. Esto creará una fuente de materiales económicos para las industrias
textil y papelera. Una variable estudiada es X, el porcentaje del contenido
en ceniza de una determinada turbera. Supongamos que una muestra
aleatoria de 50 turberas produce esas observaciones:
.5
2.2
3.4
2.5
2.4
1.5
1.8
2.0
1.4
1.7
2.7
.7
4.0
3.8
1.9
5.0
4.5
3.7
1.0
3.0
2.3
1.3
2.1
1.8
2.0
2.3
1.2
3.0
2.4
1.7
a) Calcular:
i.
Media aritmética
ii.
Mediana
iii.
Moda
iv.
Percentiles
v.
Varianza
vi.
Desviación típica
vii.
Valores máximo y mínimo
b) Interpretar los valores anteriores
1.1
1.8
1.9
2.7
2.8
1.6
3.6
2.3
1.2
2.7
2.3
2.4
2.6
1.5
4.5
3.5
.8
3.1
3.2
2.1
Los resultados obtenidos son los siguientes:
Estadísticos
CENIZA
Válidos
50
Perdidos 0
N
Media
2.350
Mediana
2.300
Moda
2.3
Desv. típ.
1.0187
Varianza
1.0377
Mínimo
.5
Máximo
Percentiles
5.0
10
1.110
25
1.675
75
3.000
90
3.790
Se observa que los valores oscilan desde el 0.5 hasta el máximo, 5, con una dispersión
de 1.0187. Los valores de la media, la mediana y la moda difieren en 5 centésimas,
2.350 y 2.3.
Histograma:
CENIZA
14
12
10
8
6
Frecuencia
4
Desv. típ. = 1.02
2
Media = 2.35
N = 50.00
0
.50
1.00 1.50 2.00 2.50 3.00 3.50 4.00 4.50 5.00
CENIZA
Ejercicio 4:
Se midieron los niveles de ozono alrededor de Los Ángeles y ascendieron a
220 partes por billón (ppb). Las concentraciones de esta magnitud pueden
ocasionar quemaduras en los ojos y son peligrosas tanto para las plantas
como para la vida animal. También se obtuvieron datos del nivel de ozono en
una zona boscosa cerca de Seatle, Washington, que fueron los siguientes:
160 164 176 160 180 178 161 167 161 169
167 173 165 163 162 172 162 163 162 163
168 185 179 170 196
c) Calcular:
i.
Media aritmética
ii.
Mediana
iii.
Moda
iv.
Percentiles
v.
Varianza
vi.
Desviación típica
vii.
Valores máximo y mínimo
d) Interpretar los valores anteriores
Estadísticos
N
OZONO
Válidos
25
Perdidos
0
Media
169.04
Mediana
167.00
Moda
162(a)
Desv. típ.
9.030
Varianza
81.540
Mínimo
160
Máximo
Percentiles
196
10
160.60
25
162.00
75
174.50
90
182.00
a Existen varias modas. Se mostrará el menor de los valores.
Ejercicio 5:
Se realiza un estudio para investigar la relación entre el nivel de humedad
del suelo y la tasa de mortalidad en lombrices de tierra. La tasa de
mortalidad, y, es la proporción de lombrices de tierra que mueren tras un
periodo de dos semanas. El nivel de humedad, x, viene medido en milímetros
de agua por centímetro cuadrado de suelo. Se obtuvieron los siguientes
datos:
x
y
0.000
0.000
0.000
0.316
0.316
0.316
0.632
0.632
0.632
0.947
0.947
0.947
1.260
1.260
1.260
0.5
0.4
0.5
0.2
0.3
0.3
0.0
0.1
0.0
0.1
0.2
0.1
0.6
0.5
0.4
Se pide:
a) Nube de puntos
b) Rectas de regresión
c) Coeficiente de correlación
d) Grado de ajuste
e) Interpretación
Este tipo de gráficos presenta las siguientes alternativas:
Para seleccionar una u otra opción habrá que pulsar en el icono correspondiente y a
continuación pulsar Definir. En nuestro caso trabajaremos con el diagrama de
dispersión simple.
El gráfico que obtenemos es el siguiente:
Diagrama de dispersión
Nivel de humedad - Tasa de mortalidad
.7
.6
.5
.4
.3
.2
.1
Y
0.0
-.1
-.2
0.0
.2
.4
.6
.8
1.0
1.2
1.4
X
A partir del cual se observa claramente que no existe relación lineal entre las variables,
sino que ésta es más bien de tipo parabólica.
Una vez introducidas las variables, la ventana de regresión lineal nos permite abrir otras
cajas de diálogo y así poder calcular una serie de gráficos y estadísticos. Si pulsamos en
el botón Estadísticos,
aparece una ventana a partir de la cual podemos seleccionar varios resultados:
Correlaciones
Correlación
de Pearson
Sig.
(unilateral)
N
X
Y
1.000
-.051
Y
X
-.051
1.000
.
.428
Y
X
Y
.428
15
15
.
15
15
X
Resumen del modelo
R
R
cuadrado
R cuadrado
corregida
Error típ. de la
estimación
.051(a)
.003
-.074
.2043
En nuestro caso, obtenemos un coeficiente de correlación de Pearson de -0.051 o lo que
es equivalente un coeficiente de determinación de 0.003, lo cual reafirma la observación
anterior de que no existe relación lineal entre ambas variables.
Estadísticos de cambio
Cambio en
Cambio en F
gl1
gl2
R cuadrado
.003
.034
1
13
a Variables predictoras: (Constante), X
Sig. del
cambio en F
.856
ANOVA(b)
Modelo
1
Suma de
cuadrados
gl
Regresión
.001
1
Residual
.543
13
Total
.544
14
a Variables predictoras: (Constante), X
b Variable dependiente: Y
Media
cuadrática
.001
.042
F
.034
Sig.
.856(a)
En cualquier caso, el modelo se ha estimado y la recta de regresión de y respecto x sería:
y = - 0.22 + 0.294 x
Coeficientes(a)
Coeficientes no
estandarizados
Modelo
B
1
(Constante)
X
a Variable dependiente: Y
Error típ.
.294
.091
-.022
.118
Coeficientes
estandarizado
s
t
Sig.
Beta
-.051
3.214
.007
-.185
.856
Ejercicio 6:
Se realiza un estudio de fotoperiodismo en aves acuáticas. Se pretende
establecer una ecuación mediante la cual pueda predecirse la duración de la
estación de cría, Y, a partir del conocimiento del fotoperíodo (nº de horas
de luz por día) bajo el que se inició la reproducción, X. Se obtuvieron los
siguientes datos observando el comportamiento de once Aythya (patos
buceadores):
x
y
12.8
13.9
14.1
14.7
15.0
15.1
16.0
16.5
16.6
17.2
17.9
110
54
98
50
67
58
52
50
43
15
28
Se pide:
a) Nube de puntos
b) Rectas de regresión
c) Coeficiente de correlación
d) Grado de ajuste
e) Interpretación
Gráfico de dispersión
Duración estación cría - Fotoperíodo
120
100
80
60
40
Y
20
0
12
13
14
15
16
17
18
X
Estadísticos descriptivos
Y
56.82
Desviación
típ.
27.429
X
15.436
1.5468
Media
N
11
11
Correlaciones
Correlación de
Pearson
Y
Y
1.000
X
-.852
X
-.852
1.000
Sig. (unilateral)
Y
.
.000
X
.000
.
Y
11
11
X
11
11
N
Resumen del modelo
Modelo
1
R
.852(a)
R cuadrado
R cuadrado
corregida
.726
Error típ. de la
estimación
.696
15.132
Estadísticos de cambio
Cambio en R
cuadrado
Cambio en F
gl1
.726
23.858
1
a Variables predictoras: (Constante), X
gl2
9
Sig. del
cambio en F
.001
ANOVA(b)
Modelo
1
Regresión
Suma de
cuadrados
5462.883
1
Media
cuadrática
5462.883
228.973
gl
Residual
2060.753
9
Total
7523.636
10
a Variables predictoras: (Constante), X
b Variable dependiente: Y
F
23.858
Sig.
.001(a)