soluciones

Procesadores de lenguajes
Ejercicios del Tema 4
EJERCICIO 5.7
La siguiente gramática representa la sintaxis de la instrucción de asignación de un lenguaje
basado en conjuntos:
Asig J id igual Expr pyc
Expr J Base
Expr J Expr union Base
Expr J Expr interseccion Base
Base J llave_ab Elem llave_ce
Base J par_ab Expr par_ce
Elem J num
Elem J Elem coma num
A continuación se muestra un ejemplo de una cadena de entrada para esta gramática:
A = { 1 , 2 } ∪ ( { 3 , 4, 5 } ∩ { 3 , 5 } ) ;
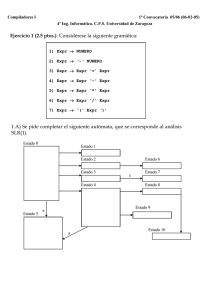
(a) Describa los estados y transiciones del autómata reconocedor de prefijos viables.
(b) Construya la tabla de análisis SLR de la gramática planteada.
SOLUCION:
(a) Describa los estados y transiciones del autómata reconocedor de prefijos viables
Estado
Elementos
0
X J * Asig
Asig J * id igual Expr pyc
1
X J Asig *
2
Asig J id * igual Expr pyc
1
Transiciones
Asig J 1
id J 2
igual J
3
Estado
3
4
Elementos
Transiciones
Asig J id igual * Expr pyc
Expr J * Base
Expr J * Expr union Base
Expr J * Expr interseccion Base
Base J * llave_ab Elem llave_ce
Base J * par_ab Expr par_ce
Expr J 4
Base J 5
Asig J id igual Expr * pyc
Expr J Expr * union Base
Expr J Expr * interseccion Base
pyc J 8
union J 9
interseccion
llave_ab J 6
par_ab J 7
5
Expr J Base *
6
Base J llave_ab * Elem llave_ce
Elem J * num
Elem J * Elem coma num
Elem J 11
num J 12
7
Base J par_ab * Expr par_ce
Expr J * Base
Expr J * Expr union Base
Expr J * Expr interseccion Base
Base J * llave_ab Elem llave_ce
Base J * par_ab Expr par_ce
Expr J 13
Base J 5
J 10
llave_ab J 6
par_ab J 7
8
Asig J id igual Expr pyc *
9
Expr J Expr union * Base
Base J * llave_ab Elem llave_ce
Base J * par_ab Expr par_ce
Base J 14
llave_ab J 6
par_ab J 7
10
Expr J Expr interseccion * Base
Base J * llave_ab Elem llave_ce
Base J * par_ab Expr par_ce
Base J 15
llave_ab J 6
par_ab J 7
11
Base J llave_ab Elem * llave_ce
Elem J Elem * coma num
llave_ce J 16
coma J 17
12
Elem J num *
13
Base J par_ab Expr * par_ce
Expr J Expr * union Base
Expr J Expr * interseccion Base
14
Expr J Expr union Base *
15
Expr J Expr interseccion Base *
16
Base J llave_ab Elem llave_ce *
17
Elem J Elem coma * num
18
Base J par_ab Expr par_ce *
19
Elem J Elem coma num *
par_ce J 18
union J 9
interseccion J
num
J 19
10
(b)
Siguientes(Asig) = { $ }
Siguientes(Expr) = { pyc, union, interseccion, par_ce }
Siguientes(Base) = { pyc, union, interseccion, par_ce }
Siguientes(Elem) = { llava_ce, coma }
Est.
id
0
d2
=
;
num
∪
∩
{
}
(
)
,
A
Ex
B
4
5
OK
d3
3
d6
4
d8
d9
d10
5
R2
R2
R2
6
d7
R2
d12
11
7
d6
d7
13
8
5
R1
9
d6
d7
14
10
d6
d7
15
11
d16
d17
12
R7
R7
13
d9
d10
d18
14
R3
R3
R3
R3
15
R4
R4
R4
R4
16
R5
R5
R5
R5
R6
R6
R6
17
18
19
El
1
1
2
$
d19
R6
R8
R8
EJERCICIO 5.17
La siguiente gramática permite describir expresiones vectoriales formadas por dos operaciones: la suma de vectores y el producto de un escalar por un vector.
Expr J Factor
Expr J Expr plus Factor
Expr J Expr minus
Factor
Factor J vector
Factor J num prod
Factor
Factor J lpar Expr rpar
(a) Construya el autómata reconocedor de prefijos viables de la gramática anterior
(b) Construya la tabla de análisis SLR de la gramática planteada. Utilice para ello la tabla
incluida en la última página.
(c) Realice la traza para el siguiente ejemplo
3 * v1 + 2 * ( v2 - 5 * v3 )
SOLUCIÓN:
(a)
Estado
0
1
Elementos
Transiciones
X J * Expr
Expr J * Factor
Expr J * Expr plus Factor
Expr J * Expr minus Factor
Factor J * vector
Factor J * num prod Factor
Factor J * lpar Expr rpar
Expr J 1
Factor J 2
X J Expr *
Expr J Expr * plus Factor
Expr J Expr * minus Factor
vector J 3
num J 4
lpar J 5
plus J 6
minus J 7
2
Expr J Factor *
3
Factor J vector *
4
Factor J num * prod
5
Factor J lpar * Expr rpar
Expr J * Factor
Expr J * Expr plus Factor
Expr J * Expr minus Factor
Factor J * vector
Factor J * num prod Factor
Factor J * lpar Expr rpar
Expr J 9
Factor J 2
6
Expr J Expr plus * Factor
Factor J * vector
Factor J * num prod Factor
Factor J * lpar Expr rpar
Factor J 10
vector J 3
num J 4
lpar J 5
7
Expr J Expr minus * Factor
Factor J * vector
Factor J * num prod Factor
Factor J * lpar Expr rpar
Factor J 11
vector J 3
num J 4
lpar J 5
8
Factor J num prod * Factor
Factor J * vector
Factor J * num prod Factor
Factor J * lpar Expr rpar
Factor J 12
vector J 3
num J 4
lpar J 5
9
Factor J lpar Expr * rpar
Expr J Expr * plus Factor
Expr J Expr * minus Factor
rpar J 13
plus J 6
minus J 7
10
Expr J Expr plus Factor *
11
Expr J Expr minus Factor *
Factor
prod J
8
vector J 3
num J 4
lpar J 5
Estado
Elementos
Transiciones
12
Factor J num prod Factor *
13
Factor J lpar Expr rpar *
(b)
Siguientes(Expr) = { $, plus, minus, rpar }
Siguientes(Factor) = { $, plus, minus, rpar }
Estado
plus
minus
0
num
prod
d4
lpar
rpar
d5
vector
$
d3
1
d6
d7
2
r1
r1
r1
r1
3
r4
r4
r4
r4
Expr
Factor
1
2
9
2
OK
4
d8
5
d4
d5
d3
6
d4
d5
d3
10
7
d4
d5
d3
11
8
d4
d5
d3
12
9
d6
d7
d13
10
r2
r2
r2
r2
11
r3
r3
r3
r3
12
r5
r5
r5
r5
13
r6
r6
r6
r6