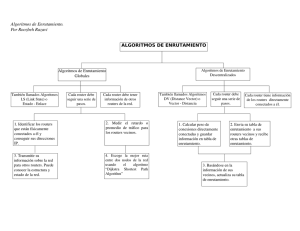
Roles del DR y BDR en el protocolo de enrutamiento OSPF

Roles del DR y BDR en el protocolo de enrutamiento OSPF
Cuando varios routers estan conectados a un segmento de red del tipo broadcast (como las redes Ethernet), uno
de estos routers del segmento tomará el control y mantendrá las adyacencias entre todos los routers de ese segmento.
Ese router toma el nombre de DR (Designated Router) y será elegido a través de la información que contienen los
mensajes hello que se intercambian los routers. Para una ecaz redundancia también se elige un router designado de
reserva ó BDR. Los DR son creados en enlaces multiacceso debido a que el número de adyacencias incrementaría
de manera signicativa el tráco de la red, de esta forma el DR y el BDR terminan reduciendo la cantidad de las
mismas y optimizando el ancho de banda y los recursos de hardware de los routers.
En el caso de no tener DR y BDR la cantidad de adyacencias que se establecerian en una topología como la
de la gura se reeja en la fórmula:
n
X
(i − 1) =
i=1
n(n − 1)
2
Entonces, si tenemos por ejemplo 4 routers la cantidad de adyacencias sin DR y
(1 − 1) + (2 − 1) + (3 − 1) + (4 − 1) =
BDR
serian:
4(4 − 1)
=6
2
Esta forma de añadir adyacencias consumiría gran cantidad de ancho de banda, recursos de memoria y CPU
de los routers. El propósito de este método es reducir al máximo este consumo de recursos haciendo que todos
los demás routers establezcan adyacencias con el. Entonces, utilizando el sistema anteriormente mencionado la
cantidad de adyacencias en redes multiacceso se limita a:
n−1=3
El DR recibe actualizaciones y las distribuye a todos los demás routers del segmento asegurándose con acuses
de recibo (ack´s) de que éstos han recibido correctamente dichas actualizaciones y poseen una copia sincronizada
de la LSDB. Los routers notican los cambios a través de la direccion multicast 224.0.0.6 a su vez el DR envía
las LSA a los routers por la direccion 224.0.0.5. El BDR escucha pasivamente y mantiene una tabla de relación
con todos los demás routers, en el caso de que el DR deje de enviar hello el BDR tomará el papel del DR.
Hacemos a continuación una obvia demostración de que el número de adyancias disminuye con el DR y BDR
usando el método de inducción:
P (n) :
n
X
n(n − 1)
≥ n − 1 ∀n ∈ N
(i − 1) =
2
i=1
P (1) :
1(1 − 1)
=0=1−1=0
2
1
P (n) ⇒ P (n + 1) : P (n) es verdadero
n + 1(n + 1 − 1)
≥n+1−1⇒
2
n(n − 1)
(n + 1)n
(n + 1)n
≥
≥n−1⇒
+ 1 ≥ n ∀n ∈ N
2
2
2
2