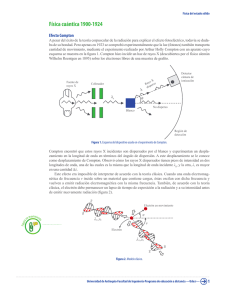
Efecto Compton

Compton nació en Wooster (Ohio) y estudió en el Wooster College y en la Universidad de
Princeton. En 1923 fue profesor de física en la Universidad de
Chicago. Durante su estancia en esta universidad, Compton dirigió
el laboratorio en el que se produjo la primera reacción nuclear en
cadena, lo que provocó que tuviera un papel relevante en el
Proyecto Manhattan, la investigación que desarrolló la primera
bomba atómica.
Desde 1945 hasta 1953 Compton fue rector de la Universidad de
Washington y después de 1954 fue catedrático de Filosofía
Natural.
Investigaciones científicas
Sus estudios de los rayos X le llevaron a descubrir en 1922
el denominado efecto Compton. El efecto Compton es el cambio de
longitud de onda de la radiación electromagnética de alta energía al ser difundida por los electrones.
El descubrimiento de este efecto confirmó que la radiación electromagnética tiene propiedades tanto
de onda como de partículas, un principio central de la teoría cuántica.
Por su descubrimiento del efecto Compton y por su investigación de los rayos cósmicos y de la
reflexión, la polarización y los espectros de los rayos X compartió el Premio Nobel de Física de
1927 con el físico británico Charles Wilson.
Reconocimientos
En su honor, así como en el de su hermano Karl Taylor Compton, se bautizó al cráter
Compton de la Luna así como el asteroide (52337) Compton, descubierto el 2 de septiembre de
1992 por Freimut Börngen y Lutz D. Schmadel.
Obras



Los rayos X y los electrones (X-Rays and Electrons, 1926)
The Freedom of Man (La libertad del hombre), 1935
Los rayos X en la teoría y en la práctica experimental (X-Rays in Theory and Experiment, 1935),
escrito en colaboración con S. K. Allison
 Human Meaning of Science (El significado humano de la ciencia), 1940
Efecto Compton
El efecto Compton consiste en el aumento de la longitud de onda de un fotón de rayos X cuando
choca con un electrón libre y pierde parte de su energía. La frecuencia o la longitud de onda de la
radiación dispersada depende únicamente de la dirección de dispersión.
o
Descubrimiento y relevancia histórica
El Efecto Compton fue estudiado por el físico Arthur Compton en 1923, quién pudo explicarlo
utilizando la noción cuántica de la radiación electromagnética como cuantos de energía. El efecto
Compton constituyó la demostración final de la naturaleza cuántica de la luz tras los estudios de
Planck sobre el cuerpo negro y la explicación de Albert Einstein del efecto fotoeléctrico. Como
consecuencia de estos estudios Compton ganó el Premio Nobel de Física en 1927.
Este efecto es de especial relevancia científica, ya que no puede ser explicado a través de la
naturaleza ondulatoria de la luz. La luz debe comportarse como partículas para poder explicar estas
observaciones, por lo que adquiere una dualidad onda corpúsculo característica de la mecánica
cuántica.
Formulación matemática
La variación de longitud de onda de los fotones dispersados, Δλ, puede calcularse a través de la
relación de Compton:
donde h es la constante de Planck, me es la masa del electrón, c es la velocidad de la luz y θ es el
ángulo entre los fotones incidentes y dispersados.
Esta expresión proviene del análisis de la interacción como si fuera una colisión elástica y su
deducción requiere únicamente la utilización de los principios de conservación de energía y
momento. La cantidad h / mec = 0.0243 Å, se denomina longitud de onda de Compton. Para los
fotones dispersados a 90º, la longitud de onda de los rayos X dispersados es justamente 0.0243 Å
mayor que la línea de emisión primaria.
Efecto Compton inverso
También puede ocurrir un Efecto Compton inverso; es decir, que los fotones disminuyan su
longitud de onda al chocar con electrones. Pero para que esto suceda es necesario que los electrones
viajen a velocidades cercanas a la velocidad de la luz y que los fotones tengan altas energías.
La principal diferencia entre los dos fenómenos es que durante el Efecto Compton "convencional",
los fotones entregan energía a los electrones, y durante el inverso sucede lo contrario.
Este efecto puede ser una de las explicaciones de la emisión de rayos X en supernovas, quasars y
otros objetos astrofísicos de alta energía.
Simulacion experimental de efecto Compton.
"http://es.wikipedia.org/wiki/Efecto_Compton"
Categorías: Fenómenos electromagnéticos | Mecánica cuántica | Electrodinámica cuántica
Cuando se analiza la radiación electromagnética que ha pasado por una región en la que hay
electrones libres, se observa que además de la radiación incidente, hay otra de frecuencia menor. La
frecuencia o la longitud de onda de la radiación dispersada depende de la dirección de la dispersión.
Sea  la longitud de onda de la radiación incidente, y ’ la longitud de onda de la radiación
dispersada. Compton encontró que la diferencia entre ambas longitudes de onda estaba determinada
únicamente por el ángulo  de dispersión, del siguiente modo
donde c es una constante que vale 2.4262 10-12 m
Se explica el efecto Compton en términos de la interacción de la radiación electromagnética con
electrones libres, que suponemos inicialmente en reposo en el sistema de referencia del observador.
Fundamentos físicos
En el efecto fotoeléctrico solamente hemos considerado que el fotón tiene una energía
E=hf . Ahora bien, un fotón también tiene un momento lineal p=E/c.
Esta relación no es nueva, sino que surge al plantear las ecuaciones que describen las
ondas electromagnéticas. La radiación electromagnética tiene momento y energía. Cuando
analicemos cualquier proceso en el que la radiación electromagnética interactúa con las partículas
cargadas debemos de aplicar las leyes de conservación de la energía y del momento lineal.
En el caso del efecto fotoeléctrico, no se aplicó la ley de conservación del momento
lineal por que el electrón estaba ligado a un átomo, a una molécula o a un sólido, la energía y el
momento absorbidos están compartidos por el electrón y el átomo, la molécula o el sólido con los
que está ligado.
Vamos a obtener la fórmula del efecto Compton a partir del estudio de un choque
elástico entre un fotón y un electrón inicialmente en reposo.
1. Principio de conservación del momento lineal

Sea p el momento lineal del fotón incidente,


Sea p' el momento lineal del fotón difundido,
Sea pe es el momento lineal del electrón después del choque, se verificará que
p=p'+pe (1)
2. Principio de conservación de la energía



La energía del fotón incidente es E=hf .
La energía del fotón dispersado es E’=hf ’ .
La energía cinética del electrón después del choque no la podemos escribir como mev2/2 ya
que el electrón de retroceso alcanza velocidades cercanas a la de la luz, tenemos que
reemplazarla por la fórmula relativista equivalente
donde me es la masa en reposo del electrón 9.1·10-31 kg
El principio de conservación de la energía se escribe
(2)
Resolviendo el sistema de ecuaciones (1) y (2) llegamos a la siguiente expresión
Teniendo en cuanta la relación entre frecuencia y longitud de onda se convierte en la expresión
equivalente
Hemos obtenido el valor de la constante de proporcionalidad c a partir de las constantes
fundamentales h, me y c.
Llegamos entonces a la conclusión de que podemos explicar la dispersión de la radiación
electromagnética por los electrones libres como una colisión elástica entre un fotón y un electrón en
reposo en el sistema de referencia del observador. A partir de las ecuaciones de conservación del
momento lineal y de la energía, llegamos a la ecuación que nos relaciona la longitud de onda de la
radiación incidente  con la longitud de onda de la radiación dispersada ’ y con el ángulo de
dispersión  .
Actividades
En la experiencia real, el detector es un cristal de INa,
la fuente de rayos gamma está producida por el isótopo
Cs-137, que tiene un pico muy agudo centrado en
661.6 keV, o en la longitud de onda 1.878 10-12 m,
(0.01878 A). Los electrones libres los proporciona un
trozo de metal que puede ser una varilla de hierro.
Midiendo la diferencia de longitudes de onda entre la radiación dispersada y la radiación incidente
se pide calcular la constante C. A partir del valor de esta constante, y conocida los valores de las
constantes fundamentales, velocidad de la luz c=3·108 m/s y la masa del electrón me=9.1·10-31 kg,
se pide calcular el valor de la constante h de Planck, comprobando que está cerca del valor
6.63·10-34 Js.
Se pulsa el botón titulado Nuevo

Se cambia el ángulo  del detector actuando con el ratón,
Se mide la longitud de onda de la radiación dispersada.
Ejemplo:
La longitud de onda de la radiación dispersada para el ángulo 60º es '=0.03091 A.
Calcular la constante C y a continuación, la constante h de Planck.
0.03091-0.01878=C(1-cos60)
C=0.02426 A=2.426·10-12 m
En la parte inferior izquierda del applet, se representa la intensidad de la radiación gamma
que registra el detector en función de la longitud de onda. En el programa interactivo, la fuente de
rayos gamma emite ondas electromagnéticas cuyas longitudes de onda están centradas en 0.01878
A. La forma del pico se ha representado mediante la gaussiana
centrada en dicha longitud de onda a, y cuyo valor sigma  se ha ajustado para dar la apariencia de
un pico agudo (en color azul). La radiación registrada por el detector se ha representado por medio
de otra gaussiana (en color rojo) centrada en la longitud de onda dispersada cuyo valor de sigma 
va creciendo con el ángulo de dispersión.
En la parte superior derecha del applet, se muestran los valores numéricos de las
longitudes de onda en angstrong (10-10 m) de la radiación incidente y dispersada.
En la parte derecha del applet, podemos ver de forma animada el choque elástico entre un
fotón y un electrón en reposo. Podemos apreciar gráficamente cómo cambia la longitud de onda de
la radiación dispersada a medida que aumenta el ángulo de dispersión.
Podemos ver también que el electrón retrocede adquiriendo un momento lineal pe y
formando un ángulo que se puede calcular a partir de las ecuaciones de conservación del momento
lineal (1) y de la energía (2). Para calcular la velocidad v del electrón, necesitamos la expresión
relativista del momento lineal
Actuar con el puntero del ratón sobre el detector para cambiar el ángulo de observación
Referencias
La descripción de la experiencia real se encuentra en University Laboratory Experiments. Physics.
Volume 3. PHYWE. Pág. 5.2.12.
Problemas de aplicación.
Efecto Fotoeléctrico y Efecto Compton
1. El fotón
(a) ¿Cuánto vale la energía de un fotón de luz roja? (_λ = 650 nm)?.
(b) ¿Cuánto vale su momento?
(c) ¿Cuánto vale la longitud de onda de un fotón de 2.4 eV?
(d) La intensidad mínima de luz que puede percibir el ojo humano es
Cuántos fotones por segundo entran en el ojo a esa intensidad?
W/m2.
2. Efecto Fotoeléctrico
2.1.- Un haz de un láser, con una intensidad de 120 W/m2 incide sobre una superficie de Sodio. Suponiendo
que un electrón en esa superficie está confinado en un ´área de radio igual al radio del átomo de Sodio,
¿Cuánto tardará en emitirse el primer fotoelectrón?
Datos: Función de trabajo de Na W = 2.3 eV, λNa = 1 °A. 1 eV = 1.6 × 10−19 J.
2.2.- La función de trabajo del Tungsteno es _ = 4.52 eV.
i. ¿Cuál es la longitud de onda de corte? ¿En qué rango del espectro electromagnético está?
ii. Cuál es la máxima energía cinética de los fotoelectrones si λ = 198 nm?
iii. ¿Cuál es el potencial de frenado en ese caso?
2.3.- El potencial de frenado para fotoelectrones emitidos desde una superficie iluminada con luz de longitud
de onda λ = 4910 °A es 0.71V. Cuando se cambia la longitud de onda incidente, se encuentra que el
potencial de frenado es 1.43V . Calcular la nueva longitud de onda y la función de
trabajo del metal.
Respuesta: λ = 3.82 × 10−7 m; W = 1.82 eV.
2.4.- ¿Qué tan efectivo es un cuerpo negro a una temperatura de 500 °K, para producir fotoelectrones en un
metal cuya función de trabajo W = 0.214 eV ?
Efecto Compton
1.- Un fotón de 60 keV incide sobre un electrón libre. Encontrar la máxima energía que puede tener el fotón
dispersado, y su longitud de onda.
2.- Radiación de 1 °A hace dispersión Compton con una placa de Carbón. La radiación dispersada se
observa en una dirección perpendicular a la incidente.
2.1.- ¿Cuánto vale la longitud de onda dispersada?
2.2.- ¿Cuánto vale la energía cinética del electrón
2.3.- ¿A qué ángulo se dispersa el electrón?
3.- Rayos X de 0.24 nm son dispersados (Compton) y se observa el rayo dispersado a 60° relativos al rayo
incidente. Encontrar:
3.1.- la longitud de onda de los rayos X dispersados
3.2.- la energía de los fotones dispersados
3.3.- la energía cinética de los electrones dispersados
4.- el ángulo de dispersión de los electrones.
Los rayos X con longitud de onda λ y energía E son dispersados elásticamente
por electrones libres (de masa me) que están inicialmente en reposo. Se
observan fotones dispersados con una longitud de onda λ´ (y energía E0).
La energía cinética máxima que pueden tener los electrones Kmax es:
a)
b)
c)
d)
d) Ninguna de las anteriores.
5.-Calcular el ángulo con que se dispersa un fotón de 20 MeV por un electrón libre, si pierde un 10% de su
energía inicial
(Respuesta: 44.29°)