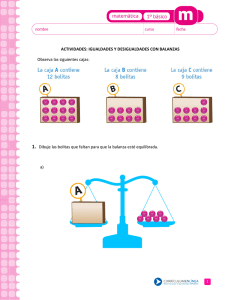
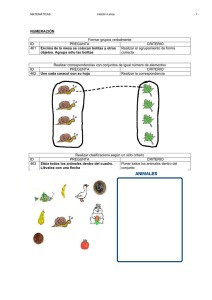
¿De cuántas maneras pueden colocarse 33 bolitas

¿De cuántas maneras pueden colocarse 33 bolitas indistingibles en 7 cajas
distintas si en la primera caja debe haber a lo sumo 3 bolitas y en la segunda
caja debe haber más bolitas que en la primera?
Para resolver este ejercicio nos va a convenir separar en 4 casos y luego
sumarlos al final.
Caso
Caso
Caso
Caso
1:
2:
3:
4:
Nunguna bolita el la caja 1
1 bolita en la caja 1
2 bolitas en la caja 1
3 bolitas en la caja 1
Caso 1: Nunguna bolita el la caja 1
Si la caja 1 contiene 0 bolitas, entonces la caja 2 debe tener al menos 1.
Separamos la caja 1 dejandola vacia e introducimos una bolita en la caja 2.
De esta manera nos queda el siguiente ecenario...
32 bolitas para repartir entre 6 cajas
La forma de contar la cantidad de formas que tenemos de ubicar éstas 32
bolitas en las 6 cajas, se resume a tomar los separadores de las cajas y las 32
bolitas como elementos a permutar de todas las formas posibles...
◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦ | | | | |
De esta manera nos quedarán 37 objetos de los cuales hay que contar de
cuantas formas se pueden tomar 5 de ellos...
37
5
!
Caso 2: 1 bolita el la caja 1
Si la caja 1 contiene 1 bolita, entonces la caja 2 debe tener al menos 2.
Separamos la caja 1 dejandola agregandole ahora 1 bolita e introducimos 2
bolitas en la caja 2.
1
De esta manera nos queda el siguiente ecenario...
30 bolitas para repartir entre 6 cajas
La forma de contar la cantidad de formas que tenemos de ubicar éstas 30
bolitas en las 6 cajas, se resume a tomar los separadores de las cajas y las 30
bolitas como elementos a permutar de todas las formas posibles...
◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦ | | | | |
De esta manera nos quedarán 35 objetos de los cuales hay que contar de
cuantas formas se pueden tomar 5 de ellos...
35
5
!
Caso 3: 2 bolitas el la caja 1
Si la caja 1 contiene 2 bolita, entonces la caja 2 debe tener al menos 3.
Separamos la caja 1 dejandola agregandole ahora 2 bolitas e introducimos 3
bolitas en la caja 2.
De esta manera nos queda el siguiente ecenario...
28 bolitas para repartir entre 6 cajas
La forma de contar la cantidad de formas que tenemos de ubicar éstas 28
bolitas en las 6 cajas, se resume a tomar los separadores de las cajas y las 28
bolitas como elementos a permutar de todas las formas posibles...
◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦| | | | |
De esta manera nos quedarán 33 objetos de los cuales hay que contar de
cuantas formas se pueden tomar 5 de ellos...
33
5
2
!
Caso 4: 3 bolitas el la caja 1
Si la caja 1 contiene 3 bolita, entonces la caja 2 debe tener al menos 4.
Separamos la caja 1 dejandola agregandole ahora 3 bolitas e introducimos 4
bolitas en la caja 2.
De esta manera nos queda el siguiente ecenario...
26 bolitas para repartir entre 6 cajas
La forma de contar la cantidad de formas que tenemos de ubicar éstas 26
bolitas en las 6 cajas, se resume a tomar los separadores de las cajas y las 26
bolitas como elementos a permutar de todas las formas posibles...
◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦◦| | | | |
De esta manera nos quedarán 31 objetos de los cuales hay que contar de
cuantas formas se pueden tomar 5 de ellos...
31
5
!
Solo nos resta sumar los cuatro casos...
Rta =
37
5
!
+
35
5
!
+
3
33
5
!
+
31
5
!