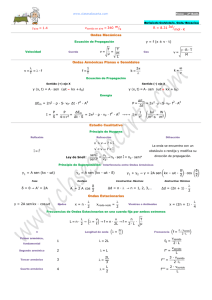
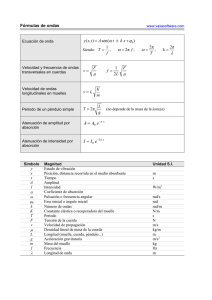
ψ ψ ψ ψ π π λ π λ λ λ

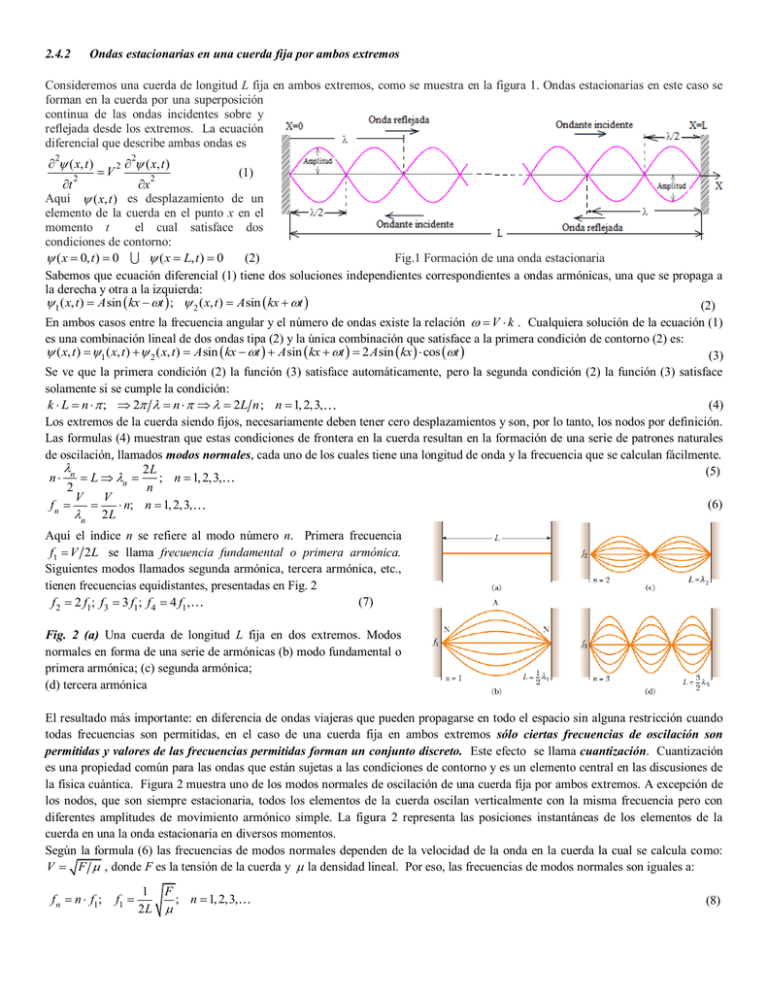
2.4.2
Ondas estacionarias en una cuerda fija por ambos extremos
Consideremos una cuerda de longitud L fija en ambos extremos, como se muestra en la figura 1. Ondas estacionarias en este caso se
forman en la cuerda por una superposición
continua de las ondas incidentes sobre y
reflejada desde los extremos. La ecuación
diferencial que describe ambas ondas es
  ( x, t )
2
V
2
  ( x, t )
2
(1)
2
2
t
x
Aquí  ( x, t ) es desplazamiento de un
elemento de la cuerda en el punto x en el
momento t
el cual satisface dos
condiciones de contorno:
(2)
Fig.1 Formación de una onda estacionaria
 ( x  0, t )  0
 ( x  L, t )  0
Sabemos que ecuación diferencial (1) tiene dos soluciones independientes correspondientes a ondas armónicas, una que se propaga a
la derecha y otra a la izquierda:
1 ( x, t )  A sin  kx  t  ;  2 ( x, t )  A sin  kx  t 
(2)
En ambos casos entre la frecuencia angular y el número de ondas existe la relación   V  k . Cualquiera solución de la ecuación (1)
es una combinación lineal de dos ondas tipa (2) y la única combinación que satisface a la primera condición de contorno (2) es:
 ( x, t )  1 ( x, t )  2 ( x, t )  A sin  kx  t   A sin  kx  t   2 A sin  kx   cos t 
(3)
Se ve que la primera condición (2) la función (3) satisface automáticamente, pero la segunda condición (2) la función (3) satisface
solamente si se cumple la condición:
(4)
k  L  n   ;  2   n      2L n ; n  1, 2,3,
Los extremos de la cuerda siendo fijos, necesariamente deben tener cero desplazamientos y son, por lo tanto, los nodos por definición.
Las formulas (4) muestran que estas condiciones de frontera en la cuerda resultan en la formación de una serie de patrones naturales
de oscilación, llamados modos normales, cada uno de los cuales tiene una longitud de onda y la frecuencia que se calculan fácilmente.

2L
(5)
n  n  L  n 
; n  1, 2,3,
2
n
V
V
(6)
fn 

 n; n  1, 2,3,
n 2 L
Aquí el índice n se refiere al modo número n. Primera frecuencia
f1  V 2L se llama frecuencia fundamental o primera armónica.
Siguientes modos llamados segunda armónica, tercera armónica, etc.,
tienen frecuencias equidistantes, presentadas en Fig. 2
(7)
f 2  2 f1; f3  3 f1; f 4  4 f1,
Fig. 2 (a) Una cuerda de longitud L fija en dos extremos. Modos
normales en forma de una serie de armónicas (b) modo fundamental o
primera armónica; (c) segunda armónica;
(d) tercera armónica
El resultado más importante: en diferencia de ondas viajeras que pueden propagarse en todo el espacio sin alguna restricción cuando
todas frecuencias son permitidas, en el caso de una cuerda fija en ambos extremos sólo ciertas frecuencias de oscilación son
permitidas y valores de las frecuencias permitidas forman un conjunto discreto. Este efecto se llama cuantización. Cuantización
es una propiedad común para las ondas que están sujetas a las condiciones de contorno y es un elemento central en las discusiones de
la física cuántica. Figura 2 muestra uno de los modos normales de oscilación de una cuerda fija por ambos extremos. A excepción de
los nodos, que son siempre estacionaria, todos los elementos de la cuerda oscilan verticalmente con la misma frecuencia pero con
diferentes amplitudes de movimiento armónico simple. La figura 2 representa las posiciones instantáneas de los elementos de la
cuerda en una la onda estacionaria en diversos momentos.
Según la formula (6) las frecuencias de modos normales dependen de la velocidad de la onda en la cuerda la cual se calcula como:
V  F  , donde F es la tensión de la cuerda y  la densidad lineal. Por eso, las frecuencias de modos normales son iguales a:
f n  n  f1;
f1 
1
2L
F

; n  1, 2,3,
(8)
Las fórmulas similares son válidas también para ondas estacionarias en una barra de material sólido con una solo diferencia
relacionada con el cálculo la velocidad de ondas, la cual en este caso se calcula como: V  Y  , donde Y es el módulo de Young y y
 la densidad volumetrical. Por eso, las frecuencias de modos normales ñarra una barra de longitud L fija por ambos extremos son
iguales a:
f n  n  f1;
2.4.3
f1 
1 Y
; n  1, 2,3,
2L 
(9)
Ondas estacionarias en una cuerda fija en un solo extremo
Consideremos una cuerda de longitud L fija en un solo extremo, como se muestra en la
figura 3. Ondas estacionarias en este caso se forman en la cuerda por una
superposición continua de las onda incidente sobre y reflejada desde un solo extremo.
La ecuación diferencial que describe ambas ondas es
  ( x, t )
2
t
2
V
2
  ( x, t )
2
x
2
(10)
es desplazamiento de un elemento de la cuerda en el
 ( x, t ) Aquí
punto x en el momento t el cual satisface dos condiciones de contorno:
 ( L, t )
(11)
Fig.3 Formación de una onda estacionaria
 (0, t )  0
0
x
La primera condición muestra que en extremo fijo no hay ningún desplazamiento en la dirección vertical mientras que la segunda está
relacionada con el hecho que en el extremo contrario libre no hay la fuerza elástica recuperadora en la dirección vertical. Por otro lado
las condiciones de frontera (11) muestran que en un extremo (de izquierda) siempre se ubica un nodo, mientras que en otro (de
derecha) hay un antinodo. Sabemos que ecuación diferencial (10) tiene dos soluciones independientes correspondientes a ondas
armónicas, una que se propaga a la derecha y otra a la izquierda:
1 ( x, t )  A sin  kx  t  ;  2 ( x, t )  A sin  kx  t 
(12)
En ambos casos entre la frecuencia angular y el número de ondas existe la relación   V  k . Cualquiera solución de la ecuación (11)
es una combinación lineal de dos ondas tipa (2) y la única combinación que satisface a la primera condición de contorno (11) es:
 ( x, t )  1 ( x, t )  2 ( x, t )  A sin  kx  t   A sin  kx  t   2 A sin  kx   cos t 
(13)
Se ve que la primera condición (11) la función (13) satisface automáticamente, pero la segunda condición (11) la función (13)
satisface solamente si se cumple la condición:
(14)

2

4L
k  L   2n  1 ; 
 L   2n  1   
; n  1, 2,3,
2

2
2n  1
Las formulas (14) muestran que en una cuerda fija en un solo extremo también se forma una serie de patrones naturales de oscilación,
llamados modos normales, cada uno de los cuales tiene una longitud de onda y la frecuencia que se calculan fácilmente.

4L
; n  1, 2,3,
 2n  1  n  L  n 
(15)
2
2n  1
V
V
fn 

 (2n  1); n  1, 2,3,
(16)
n 4 L
Aquí el índice n se refiere al modo número n. Primera frecuencia f1  V 4L se llama frecuencia fundamental o primera armónica.
Siguientes modos llamados segunda armónica, tercera armónica, etc., tienen frecuencias equidistantes, distanciadas cada una de la
anterior al valor 2 f1 :
(17)
f 2  3 f1; f3  5 f1; f 4  7 f1,
Fig. 4 (a) Una cuerda de longitud L fija en un solo extremo. Modos normales en forma de una
serie de armónicas (b) modo fundamental o primera armónica; (c) segunda armónica;
(d) tercera armónica
Vemos que en el caso de una cuerda fija en un solo extremo igual como en el caso anterior sólo
ciertas frecuencias de oscilación son permitidas y valores de las frecuencias permitidas
forman un conjunto discreto es decir también están cuantizadas. La figura 4 representa las posiciones instantáneas de los elementos
de la cuerda en una la onda estacionaria en diversos momentos para primeras tres armónicas.
Según la formula (6) las frecuencias de modos normales dependen de la velocidad de la onda en la cuerda la cual se calcula como:
V  F  , donde F es la tensión de la cuerda y  la densidad lineal. Por eso, las frecuencias de modos normales son iguales a:
f n  (2n  1)  f1;
f1 
1
4L
F

; n  1, 2,3,
(18)
2.4.3.1 Ondas estacionarias en tubos sonoros
Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por
un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido. Las versiones modernas de estos instrumentos de
viento son las flautas, las trompetas y los clarinetes, todos ellos desarrollados de forma que el intérprete produzca muchas notas dentro
de una amplia gama de frecuencias acústicas. El órgano es un instrumento formado por muchos tubos en los que cada tubo da una sola
nota. El órgano de la sala de conciertos de La Sydney Opera House terminado en 1979 tiene 10500 tubos controlados por la acción
mecánica de 5 teclados y un pedalero. El tubo de órgano es excitado por el aire que entra por el extremo inferior. El aire se transforma
en un chorro en la hendidura entre el alma (una placa transversal al tubo) y el labio inferior. El chorro de aire interacciona con la
columna de aire contenida en el tubo. Las ondas que se propagan a lo largo de la corriente turbulenta mantienen una oscilación
uniforme en la columna de aire haciendo que el tubo suene. Ya hemos visto en este capítulo como son las ondas estacionarias en una
cuerda. Ahora veremos las ondas estacionarias que se producen en los tubos abiertos o cerrados por un extremo.
Tubos abiertos
Si un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura 5, se representan
los tres primeros modos de vibración. Como la distancia entre dos nodos o entre dos antinodos es media
longitud de onda y la longitud del tubo es L, tenemos que para primeras tres armónicas deben cumplirse
las relaciones: L   / 2, L  , L  3 / 2 y en general L  n   / 2 , donde n es un número entero.
Considerando que la longitud de onda es igual a   V / f (velocidad del sonido dividido la frecuencia),
las frecuencias y correspondientes longitudes de onda de los distintos modos de vibración responden a la
fórmula:
Fig.5 Ondas estacionarias en tubo abierto
2L
V
(19)
n 
 fn 
n, n  1, 2,3,
n
2L
Tubos cerrados en un extremo
Si el tubo esta cerrado en un extremo se origina un antinodo en el extremo abierto por donde penetra
el aire y un nodo en el extremo cerrado. Como la distancia entre un antinodo y un nodo consecutivo
es  4 entonces la longitud L del tubo como se puede ver en las figura 6 debe cumplir para primeras
tres armónicas las siguientes condiciones L   / 4, L  3 / 4, L  5 / 4 y en general para
armónica número n L  (2n 1)   / 4 con n  1, 2, 3, ... .
Considerando que la longitud de onda es igual a   V / f (velocidad del sonido dividido la
frecuencia), las frecuencias y correspondientes longitudes de onda de los distintos modos de
vibración responden a la fórmula:
Fig.6 Ondas estacionarias en tubo cerrado
4L
V
(20)
n 
 fn 
(2n  1), n  1, 2,3,
2n  1
4L
Si gas en tubo puede considerarse como un gas ideal con masa molecular M [kg/mol] y temperatura T, la velocidad del sonido es
V 
3RT
J
;   1.4; R  8.314
M
K  mol
(21)
Leyes de Bernoulli
Las fórmulas obtenidas explican las denominadas leyes de Bernoulli:
La frecuencia del sonido en un tubo es:
1. Directamente proporcional a la velocidad del sonido vs en el gas que contiene el tubo
2. Inversamente proporcional a la longitud del tubo L
3. En un tubo abierto, se puede producir el sonido que corresponde a la frecuencia fundamental (n=1) y sus armónicos (n=2, 3,
4, ..)
4. En un tubo cerrado, se puede producir el sonido que corresponde a la frecuencia fundamental y los armónicos impares
(2n+1=3, 5, 7, ...).
5. En dos tubos idénticos y con el mismo gas, uno abierto y otro cerrado, el abierto produce un sonido cuya frecuencia
(fundamental) es el doble que la del cerrado.