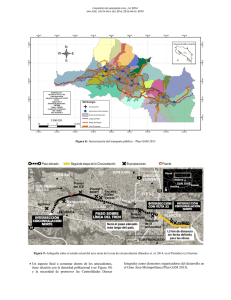
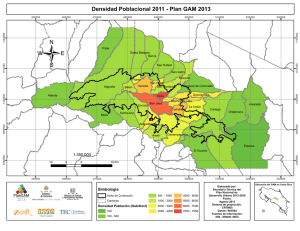
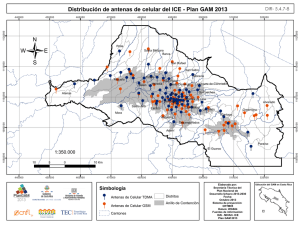
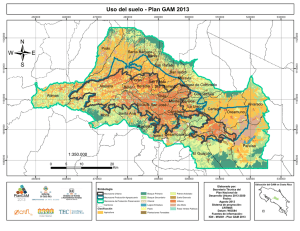
Modelo aditivo generalizado GAM:

Modelo aditivo generalizado GAM:
Regresión no lineal y no paramétrica
ISBN: 978-607-28-0154-7
Isabel Quintas
El modelo aditivo generalizado, presentado por Hastie y Tibshirani en 1990, es una extensión de
los modelos tradicionales de regresión lineal para el análisis de los datos, que incorpora la no
linealidad y la regresión no paramétrica. El modelo esta construido por la suma de funciones
suaves (splines) de las variables predictoras, pudiendo ser estas variables continuas, variables
categóricas, número de casos y series de datos. A diferencia de los modelos de regresión lineal
donde se deben determinar los parámetros correspondientes a cada uno de los predictores xi, el
modelo sustituye ∑ βi xi por una suma de funciones no necesariamente lineales ∑ai fi (xi ) , donde
cada una de las fi es estimada de manera muy flexible, pudiendo estas mostrar el efecto no lineal
de esa relación. El método permite definir las funciones de manera muy general, pudiendo existir
términos como ∑ fi(xi , xj ) propuestos por el analista. Este modelo está implementado en el
lenguaje de programación R y en el paquete estadístico S, implementados por el mismo Hastie
junto con Chambers al menos desde 2011. También está disponible en los paquetes de estadística
STATA y XLSTAT.
Entre las bondades de estos modelos están la no necesidad de probar que las variables son
independientes y si tienen o no una distribución normal. Los algorítmos inclusive permiten
introducir indicaciones respecto a la distribucion (binomial, poisson, y algunas otras); las funciones
de las relaciones que revelan los modelos permiten una comprensión mucho mayor que la de los
coeficientes betaes suponer la relación lineal de la regresión tradicional, ya que los efectos no son
constantes dentro del rango de variación de las variables.
Palabras claves: modelos de regresión, GAM, regresión no lineal, B-splines, lenguaje R
Introducción
Tal vez el modelo más sencillo que se puede pensar para pronosticar o evaluar como cambia el
valor de una variable que se cree está relacionada con otra, es suponer que existe una relación lineal
del tipo y ~ βx , pero si se cuenta con una serie de mediciones de ambas variables, seguramente no
será posible encontrar un valor de β que satisfaga todos los pares de valores. Esto lleva a la
necesidad de plantear un modelo estadístico lineal
115
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
y= βx +ε
(1)
y encontrar el valor de β tal que para cada par de valores se cumpla
yi = β xi + εi donde εi
es una variable random independiente del valor de x, (el error de cada estimación), tal que E(εi) =
0. Este modelo es el modelo de regresión simple que generalmente se resuelve exigiendo que β
minimice la suma de los errores cuadráticos.
Cuando el valor de la variable a estimar y, dependa de varias variables predictoras, el método
se generaliza resultando el modelo de regresión múltiple
y=
βo + β1 x1 + β2 x2 + β3 x3 +………… + βm xm + e
donde los βi
(2)
son los parámetros desconocidos del modelo que deben estimarse a partir de
los datos. Pero el modelo anterior supone una relación lineal entre los predictores y la variable a
estimar. Y no solo esto, además el modelo tambien supone a) que la variable y es una varuiable
random con distribución normal
linealmente independientes; c)
N ( ȳ, σ2);
b) las variables predictoras xi son variables
la variable que corresponde al error de cada medición ei tiene
tambien una distribución normal N ( 0, σ*2) y d) se supone que los valores de la variable a
predecir son correctos.
Pero la mayoría de los fenómenos a estudiar no necesariamente son lineales. La generalización
del modelo (2) permite, si el analista lo cree conveniente introducir por ejemplo un modelo cúbico
o puede realizar una transformación de las variables como en los siguientes ejemplos:
y=
βo + β1 x1 + β2 x12 + β3 x13 +………… + βm x2 + e
(3)
y=
βo + β1 x1 + β2 x2 + β3 log(x1.x2) +………… + βm xm + e
(4)
en el modelo (3) los estimadores son x1, x12 ,x13 y x2 mientras que en el modelo (4), y depende
linealmente del logaritmo del producto de x1
por x2. En estos casos se puede introducir cierta
alinealidad siempre que esta sea suficiemntemente obvia y sencilla como para que el analista la
descubra y la introduzca.
El modelo aditivo generalizado (GAM) propuesto por Hastie y Tibshirani en 1990 cambia. la
sumatoria de los términos de las variables del modelo lineal por una suma de funciones de las
distintas variables predictoras. La ecuación (2) del modelo de regresión lineal múltiple
116
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
y=
βo + β1 x1 + β2 x2 + β3 x3 +………… + βm xm + ε
es sustituida por un modelo no lineal y no paramético
y = bo + f1(x1) + f2 (x2 ) +..…. + f m (xm ) + ε
(5)
donde las fi(xi) son funciones polinómicas por tramos que tratan de explicar la variación de la
variable dependiente y, con la variable predictora xi quitando la parte explicada por las otras
variables. Se trata de interpolación con splines cúbicas.
La gran ventaja de este método es que el usuario no tiene que sugerir el tipo de función
exixtente entre las variables sino que es el modelo quien define la forma de esta relación, en vez
de tener que elegir un solo parámetro βi
que mejor ajuste para todo el rango de valores de la
variable correspondiente. La forma de la función quedará determinada por los datos disponibles y
por un parámetro de suavizado que establece que tan cerca la función tiene que ajustar a los puntos
dato. El modelo tambien permite el ajuste de variables con distribuciones como la Gamma, la
Poisson, la binomial, normal, etc.
A continuación se presentan los conceptos básicos de la interpolación polinomial y la
interpolación o ajuste con b-splines; finalmente se presenta un ejemplo en el que se busca el
modelo que mejor describe a un conjunto de datos utilizando la función gam( ) del lenguaje R.
Ajuste polinomial y B-splines
El ajuste polinomial utiliza la idea de representar a una función suave en términos de los
polinomios básicos
b0(x) = 1, b1(x) = x,, ,
b2(x) = x2,
b3(x) = x3, etc.
La sumatoria de k de estos polinómios básicos multiplicada por ciertos parámetros βi da
como resultado un polinomio de grado k-1. Como para definir un polinomio de grado k-1 se
necesitan k coeficientes, se puede construir un polinomio que pase exactamente k puntos. O sea,
para tener un polinomio de grado 3 se necesita cuatro coeficientes, y por lo tanto se puede
encontrar el polinomio de grado 3 que pase por cuatro puntos conocidos (xi,yi).
117
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
f(x) = ∑ βi bi(x)
donde
bi(x)
βi
es un polinomio básico
(6)
es un coeficiente
En la figura 1 se muestra la construcción de un polinomio de grado 4 a partir de cinco
polinomios básicos:
FIGURA 1
Las primeras cinco figuras representan los polinómios básicos de grado 0 a grado 4 y la última figura es
una función combinación lineal de los polinomios básicos. (ilustración tomada del libro Introducción a
GAM de Wood).
Para ajustar un conjunto de n datos, se utiliza una variante del método polinomial; se trata
ahora utilizar como funciones básica a splines cúbicas en vez de los polinómios antes
mencionados.
Una spline cúbica es una curva costruida como una suma de
secciones de
polinomios cúbicos unidos unidos en los extremos de manera tal que se genere una función
continua C2 hasta la segunda derivada. Se pueden utilizar splines de mayor grado, pero las splines
cúbicas son las más utilizadas.
En la figura 2 se muestra una spline construida con seis secciones cúbicas. En este caso se
trata de una “spline natural” ya que la curva tiene derivada segunda cero en los extremos. Los
puntos donde se unen las secciones así como los puntos extremos se denominan los puntos (de
118
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
control) de la spline. En las splines convencionales, utilizadas en graficación, estos puntos son los
puntos dato. En el caso de regresión, los puntos de la spline se pueden escoger dentro del rango de
los valores de x o se suelen escoger en determinados cualtiles, permitiendo así indicar con cuantos
segmentos se quiere construir la curva.
FIGURA 2
Spline contruida con seis segmentos de polinomios cúbicos sobre ocho puntos. (ilustración tomada del
libro Introducción a GAM de Wood).
En lo que sigue del análisis se presenta la relación entre la variable a predecir y una de las
variables predictoras para mayor claridad. El método de GAM determina una función entre la
variable a predecir y cada una de las variables predictoras, de tal manera de que cada una de ellas
explique lo mejor posible la parte no explicada por las demás variables.
Dado un conjunto de puntos dato (xi,yi) como se muestra en la figura 3 se podría ajustar ese
conjunto de puntos con la línea que indicada en la gráfioca de la izquierda, o tal vez se desee que la
línea se acerque más a los puntos como lo hace en la gráfica del centro o más aun en la gráfica de la
derecha. Esto depende de que tan suave se quiera que sea la función de ajuste, si se conoce por
ejemplo la variabilidad (ruido) que puedan tener las mediciones de los datos.
En el caso de regresión simple, el parámetro de la regresión se encuentra por el método de
minimos cuadrados, esto es que se trata de encontrar el valor mínimo de la sumatoria de los errores
al cuadrado:
Min ∑ │yi – ŷi│2
(7)
119
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
En el caso del modelo aditivo generalizado, para determinar la función que mejor ajusta a los
datos se introduce un parámetro de suavizado λ, y este aparece al modificarse el criterio de
minimización: ahora no solo se quiere minimizar la suma de los cuadrados de los errores, sino que
tambien se incluye a la curvatura de la función :
Min ∑ │f(xi) – ŷi│2 + λ ∫ f”(xi)
(8)
De donde se puede ver que si λ no es pequeño la curvatura debe ser menor para mantener
chico el segundo término de la expresión (8), pero si
λ se hce más pequeño, se hace más
impotrtante el primer término de la expresión. La figura 3 muestra la función que produce el mejor
ajuste dependiendo de la variabilidad tolerada.
FIGURA 3
Spline que ajusta a un conjunto de puntos para tres valores de λ. (ilustración tomada del libro Introducción a
GAM de Wood).
Aplicación del modelo GAM
A partir de la Encuesta a los hogares del 2008 realizada por el INEGI, se extrajeron los siguientes
datos de los jefes de los hogares: edad, sexo, años de educación formal, número de menores y de
mayores en el hogar 1 . La lista original contaba con 2 347
casos, pero más de 500 datos
correspondian a jefes de familia sin salario; asi mismo aparecian cuatro personas con más de 75
años con salarios superiores a docientos mil pesos. Estos casos se retiraron, quedando 1877 casos
en la base de datos.
1
No se consideraron los coeficientes de expanción correspondientes a esta información, sino los datos tal como venían.
120
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
Se utilizó la implementación del Modelo aditivo generalizado (GAM) del lenguaje R 2, para
buscar las relaciones entre el salario y las posibles variables predictoras: edad, educación, número
de adultos y de menores en la familia. A continuación se muestran los scripts (serie de instrucciones
para realizar las distintas tareas) que permiten obtener el modelo.
El primer paso es cargar los datos y realizar el análisis de la información, tanto los parámetros
representativos: valores medios, cuartiles, como la inspección visual.
> dato <- read.csv("datos 2008.csv")
# carga los datos y los guarda en dato
> head(dato)
# visualizar los datos, primeras lineas
sex edad educ menr sueldos mayores
1 1 40
6
1
752
4
2 1 25
3
1
756
2
3 2 27
7
2
786
1
4 1 34
6
2
798
2
5 2 57
4
0
907
2
6 2 31
6
1
933
2
> summary (dato)
> hist(dato$sueldos, n = 20)
# calcula parámetros básicos de cada variable
# histograma de la variable sueldos, figura
4
> plot(dato$sueldos, dato$edad,cex= 0.5) #grafica dispersión salario vs edad, figura 5
> plot (dato, cex=0.5)
#grafica diagramas de correlación , todas las
variables, figura 6
El sumario de datos indica que los salarios varian desde 700 pesos a más de 300 mil pesos; es mucho
más explícito ver el histograma de esta variable donde se reconoce la distribución Gamma (figura 4). El
modelo GAM necesita que se le indique la distribución de la variable respuesta.
Tal vez parezca razonable que el salario dependa de la edad; para esto puede ser útil ver el diagrama de
dispersión de ambas variables. La figura 5 muestra tal diagrama. Al igual que en la figura 4, se ve que los
salarios predominan independientemente de la edad, y no es evidente ninguna relación entre estas variables.
Inicialmente el modelo GAM fue desarrollado en el lenguaje R aunque ahora está disponoible en otros paquetes estadísticos
como SAS, STATA y otros.
2
121
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
FIGURA 4
Distribución de la variable aleatoria salario; es evidente que responde a una distribución gamma.
FIGURA 5
Diagrama de dispersión de edad vs salario.
Es interesante entonces ver las relaciones de cada para de variables, para lo que se puede
realizar la gráfica de correlaciones que se presenta en la figura 6. En estas se puede observar por
ejemplo que los de mayor educación formaltienen menos menores (posiblemente hijos), o que los
mayores salarios los tienen personas con mayor educación, aunque muchos aún con 10 años de
educación tienen salarios muy bajos. Lo que si se puede asegurar es que no parece existir ninguna
relación lineal o transformable en lineal con ninguno de estos predictores.
122
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
FIGURA 6
Diagrama de correlación entre las variables.
El modelo encontrado3 que mejor reproduce a la variable respuesta, en este caso el salario
indica que este depende de manera muy significativa de los predictores edad y años de educación
formal (p = 1.31e-15 y p < e-16) respectivamente, mientras que la cantidad de adultos en el hogar
aparece como muy poco significativa con un valor de la prueba estadística p = 0.0125. La cantidad
de menores en el hogar no aparece en el modelo. En la figura 7 se muestran las funciones f1(edad)
y f2(educación) del modelo aditivo. El modelo resultante está dado por:
Para construir el modelo y ver los resultados es necesario el siguiente conjunto de comandos (script en R): en proimer lugar
se carga la librerúia que contiene el modelo; luego se le pide que construya el modelo indicando las variables dependiente y la
variable resultado; en este caso dado que los sueldos tiene una distribución Gama se le indica con el parámetro family
3
># carga la libreria mgcv
>require(mgcv)
># genera el modelo que guarda como un objeto llamado m.gam
>m.gam <- gam(sueldos ~s(edad)+s(ed_formal), data=dato, family = Gamma(link="identity"))
> par(mfrow=c(1,2))
> plot (m.gam)
> summary(m.gam)
>gam.check(m.gam)
123
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
Sueldo = 31,368.3 + f1(edad) + f2(educación) + error
que explica el 34.7% de la
variabilidad
FIGURA 7
Gráfica de las funciones de interpolación f1(edad) y f2(educación) del modelo GAM.
De las gráficas se observa que el salario va aumentando con la edad hasta los 55 años
aproximadamente pero luego se mantiene constante aunque aumenta la franja de incertidumbre.
En el caso de la educación formal, parece no haber diferencia entre los 3 y 6 años de educación, o
sea primariapara aumentar con cierta pendiente entre 6 y 9 años (secundaria) y la curva crece
rapidamente con la educación superior. En la figura 8 se muestra la función correspondiente al
número de adultos en el domicilio; se aprecia que para menos de 5 adultos la función vale
aproximadamente cero y que a partir de alli se abre indicando que puede dar cualquier valor en ese
rango, por lo que no debe ser considerada.
FIGURA 8
Gráfica de las funciones de interpolación f3(mayores) del modelo GAM.
124
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
Los datos que permiten verificar la pertinencia del modelo son similares a los entregados por
qualquier paquete estadístico, a lo que se agrega el análisis gráfico de los errores. Las salidas
obtenidas son:
Family: Gamma
Link function: identity
Formula:
sueldos ~ s(edad) + s(ed_formal)
Parametric coefficients:
Estimate Std. Error
(Intercept) 31368.3
613.4
t value
51.14
Pr(>|t|)
<2e-16 ***
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Approximate significance of smooth terms:
edf
s(edad)
Ref.df
F
p-value
3.945 4.895 16.42 1.31e-15 ***
s(ed_formal) 8.083 8.659 50.46 < 2e-16 ***
R-sq.(adj) = 0.287 Deviance explained = 34.7%
GCV score = 0.5302 Scale est. = 0.52652 n = 1877
Method: GCV Optimizer: outer newton
full convergence after 6 iterations.
Gradient range [-1.733712e-07,2.374096e-08]
(score 0.5302036 & scale 0.5265235).
Hessian positive definite, eigenvalue range [0.0002167319,0.0002891293].
El análisis de los residuos se presenta en forma gráfica (figura 9) aunque tambien se puede pedir
otro tipo de resultados.
125
MODELO ADITIVO GENERALIZADO GAM / ISABEL QUINTAS
FIGURA 9
Análisis de residuos.
El modelo aditivo generalizado no requiere de muchos más conocimientos de estadística que
los modelos estándar de regresión, y permite acercarse a modelos no lineales sin casi ninguna
restricción a condición de tener suficientes datos. Este modelo debería incluirse en los cursos
regulares de econometría como ya se hace en varias universidades. Existe tambien material en linea
y esperamos que este texto pueda servir como una introducción a los conceptos que subyacen
detrás de las implementaciones que se encuentran en los paquetes de estadística más utilizados.
Referencias
INEGI, Encuesta a los hogares 2008, microdatos.
Hastie, T. &Tibshirani, R.,
1990. Generalized additive model with R.Editorial Chapman and Hall,
Laboratorios A T &T.
Wood, Simon N., 2005, Generalized Additive Models: an introducction with R. Versión PDF creado
con Acrobat.
IASC-ERS Summmer School on Statistical Learning. Data Mining and Regresion Tools. PROCIDA.
126