IB luego 0 12 30 1 4 30 1 4 10 01 20 1 3 IB +∃ ≠ = − − =

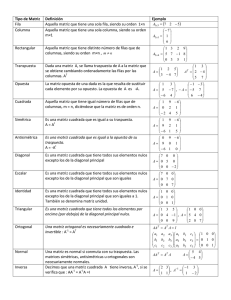
Matemáticas aplicadas a las Ciencias Sociales II
Septiembre 2006
EJERCICIO A
PROBLEMA 1. Determina la matriz A que verifica la ecuación A B + A = 2 Bt, donde
 3 − 1

B = 
0 2 
y Bt
representa la matriz traspuesta de B.
Solución:
A B + A = 2 Bt
A ( B + I ) = 2 Bt
Si existe ( B + I )-1 entonces A = 2 Bt ( B + I )-1
 3 − 1  1 0   4 − 1
 + 
 = 

B + I = 
0 2  0 1  0 3 
4 −1
= 12 ≠ 0 luego ∃ ( B + I ) −1
0 3
Calculemos la matriz inversa de (B + I)
1

3
1
 4 − 1  α i j  3 0  Ai j  3 0  A j i  3 1 


1
 → 
 → 
 → 
 → ( B + I ) −1 = 
 =  4
B + I = 
12  0 4   0
0 3 
− 1 4
1 4
0 4 


1

12 
1

3 
 3 − 1
 3 0
 luego, B t = 

Como B = 
0 2 
− 1 2
Finalmente, calculemos la matriz A,
A = 2 Bt ( B + I )-1
1
1
1 1 
 1
 3
−0 . 
3 − 0 . 0 3

 3 0   4 12 
12
3 = 2 4
 = 2 4
 
A = 2 
 − 1 + 2 . 0 − 1 + 2 1 
 − 1
 − 1 2   0 1 
3 
12
3 

 4
 4
3   6
6   3
1
 3

 
 

12  =  4
12  =  2
2
=2 4
7   − 2 14   − 1 7 
 − 1

 
 
12   4
12   2
6
 4
 3

Luego, A =  2
 − 1
 2
1

2
7

6
3 
 3


12  = 2  4
−1 2
 − 1
+ 
12 3 
 4
3


12  =
−1 8 
+ 
12 12 