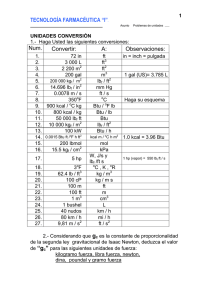
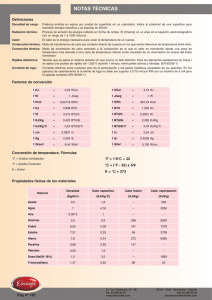
dQ=dE Q=E2E1 Wsf =(ΔE f +ΔK+ΔP) Q=ΔU=u2u1=(h2 ( p2 v2) J

PROCESO ISOMÉTRICO
Consideremos un proceso isométrico (o isocórico, o a volumen constante) que es interiormente
reversible (cuasiestático, si es sin flujo), en el que interviene una sustancia pura. En el caso de un
sistema cerrado sin flujo v = c, dQ=dudW n y dw n= p dv=0 ; por consiguiente, Q = Δu. La
ecuación de calor específicotambién da Q= c v dT. Si se consideran variedades de energía
almacenada distintas de la molecular, entonces:
∫
dQ=dE
Q= E 2−E 1
o bien
(a)
donde E = U + P + K. En un proceso isométrico de flujo constante y estado estable (por ejemplo, con
un fluido incompresible), ecuación Q=U  E f  K  PW sf se reduce a (sf indica steady
flow = flujo constante).
W sf =− E f  K  P
(b)
porque con Q = ΔU estos términos se cancelan. Es importante observar aquí que el calor Q es
independiente de si existe flujo o no, en el caso de un proceso dado. Una vez que se ha establecido
el proceso y fijado los puntos extremos del mismo, Q es constante para un fluido dado,
independientemente de si hay flujo o no.
En el caso de un gas ideal entre dos estados cualesquiera se observa que
Q = ΔU sólo para el proceso isométrico cuasiestático.
 U =∫ c v dT ; pero
La ecuación del proceso en el plano pV (o bien, pv) es V = c (o bien, v = c). Integrando ds = dQ / T =
cv dT/T, con cv constante, se obtiene:
s=c v lnT C
(c)
donde C es una constante de integración y (c) la ecuación de una curva isométrica en el plano Ts
cuando el calor específico permanece igual.
Si se tiene un vapor sobrecalentado (punto de estado 1) que se enfría a volumen constante hasta que
parte de él se condensa, los croquis en los planos pV y TS deben mostrar las líneas del líquido y
vapor saturados. En la resolución de problemas con frecuencia es necesario emplear la relación
definitoria del proceso, en este caso:
v 1=v 2=v g− y 2 v fg 2=v f  x 2 v fg 2
(d)
Mediante esta ecuación se puede hallar la calidad x2, obteniendo v1 de una tabla de vapor.
Conociendo esta calidad y una propiedad adicional, se determinan otras propiedades del vapor en 2.
Puesto que el valor de ∫ p dV es cero, el calor será:
Q=U =u 2−u 1= h2−
 p2 v 2 
p v 
 ¿−h1− 1 1 
J
J
(e)
EJEMPLO – PROCESO ISOMÉTRICO (REVERSIBLE)
Una masa de 1 lb (0.45 kg) de fluido a 15 psia (1.05 kgf/cm² abs.), 300 ºF (149 ºC) se calienta
reversiblemente [v = C hasta que su temperatura es 600 ºF (316 ºC)]. Determinar p2, Q, W, Δh y Δs si
a) El proceso es sin flujo y el fluido es (1) aire, considerado como gas ideal, o bien, (2) agua;
asimismo, resuelva el problema si el proceso es:
b) De estado estable y flujo constante con ΔP = 0, ΔK = 0 y el fluido es (1) aire, gas ideal o
bien, (2) agua.
SOLUCIÓN
a) (1) El aire como gas ideal (sin flujo): de pv = RT con v = c
p 2= p1 T 2 /T 1 =151060/ 760=20.92 psia=1.47 kgf /cm2 abs.
De B 1:
Q=U =c v T 2−T 1 =0.17141060−760=51.42 Btu/lb=28.56 kcal /kg
De las Tablas de Gas:
Q=U =183.29−129.99=53.30 Btu /lb=40 kcal /kg
De B 1:
 h=c p T 2−T 1 =0.241060−760=72 Btu /lb=40 kcal / kg
De las Tablas de Gas:
 h= h2−h1 =255.96−182.08=73.88 Btu /lb=41.04 kcal /kg
De B 1:
 s=∫ dQ /T =c v ∫ dT /T =c v ln T 2 /T 1=0.1714 ln 1060 /760=0.0570 Btu /lb · ºR=0.0570 kcal / kg · K
De las Tablas de Gas:
 s= −R ln p2 / p1=0.76496−0.68312−53.34/778ln 20.92/15=0.059 Btu /lb ·ºR=0.059 kcal /kg · K
Solución para (a) (2). Agua (sin flujo): Utilizando B 15, en el estado 1, se tiene:
v 1=29.899 ft / pd
Para el estado 2,
h 1=1192.5 Btu / pd
s1 =1.8134 Btu / pd · ºR
v 2 =v 1=29.899, t 2=600 ºF. Interpolando en B 15 se obtiene:
p 2=21.24
h 2=1334.8
 h=h 2−h 1=1.334.8−1192.5=142.3 Btu/ pd
s 2=1.9335
 s=1.9335−1.8134=0.1201 Btu / pd · ºR
u = h− pv=142.3−29.899144/ 77821.24−15=107.8 Btu / pd
W n=0
Q= u=107.8 Btu / pd
O sea, p2 = 1.49 kgf/cm² abs., Δh = 79.05 kcal/kg, Δs = 0.1201 kcal/kg · K, Q = 59.9 kcal/kg, Wn = 0.
Solución para (b) (1). Estado estable y flujo constante (ΔP = 0, ΔK = 0), aire: De (a) (1), p2 = 20.92
psia, Q sf =Q n =51.42 Btu / pd (por las tablas, 53.30).
 s=0.0570 Btu / pd · ºR (por tablas, 0.0590)
Δh = 72 Btu/pd (port ablas, 73.88)
W sf =−∫ vdp=−V  p2− p1 =−R T 2−T 1 =−53.34/7781060−760=−20.56 Btu / pd
también
W sf =− E f  P K =− E f =− pv
W sf =− h− u =−72−51.42=−20.58 Btu / pd
Es decir, p2 = 1.47 kgf/cm² abs., Δh = 40 kcal/kg, Δs = 0.0570 kcal/kg · K,
W sf =−11.42 kcal /kg.
Q sf =28.56 kcal / kg y
Solución para (b) (2). Estado estable, y flujo constante (Δp = 0, ΔK = 0), agua : De (a) (2),
p 2=21.24 psia ,Q sf =Q n=107.8 Btu / pd
 s=0.1201 Btu / pd · ºR
 h=142.3 Btu / pd
W sf =− E f  P K =− E f =− pv
W sf =− h− u =−142.3107.8=−34.5 Btu / pd
O sea:
p2 = 1.49 kgf/cm² abs.
Δh = 79.05 kcal/kg, Δs = 0.1201 kcal / kg · K
Q sf =59.88 kcal /kg
W sf =−19.16 kcal / kg
BIBLIOGRAFÍA
MORING, Faires Virgil
Termodinámica
Limusa Noriega Editores
p.p. 167 - 170
 u=107.8 Btu/ pd