© Abel Martín Una empresa fabrica únicamente tapas y envases

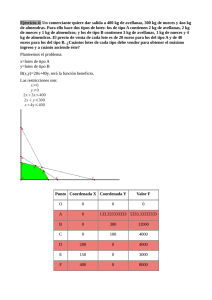
La programación lineal
135
090.– PAU – Universidad de Oviedo – Fase General – Opción A – Extraordinaria 2012
Una empresa fabrica únicamente tapas y envases. Cada lote de tapas requiere
de 1 litro de barniz y 5 minutos en el horno, mientras que cada lote de envases
requiere de 2 litros de barniz y 3 minutos en el horno. Semanalmente se dispone de
1000 litros de barniz y 3000 minutos de horno. Por restricciones de su
infraestructura, la producción semanal entre los dos productos es, como mucho, de
650 lotes.
(a) ¿Cuántos lotes de cada tipo puede fabricar la empresa cada semana? Plantea
el problema y representa gráficamente el conjunto de soluciones. ¿Se cumplirían
los requisitos si la empresa fabricase 200 lotes de tapas y 100 lotes de envases?
(b) Si la empresa vende todo lo que fabrica y gana por cada lote de tapas
fabricado 3000 euros y por cada lote de envases 4000 euros, ¿cuántos lotes de
cada tipo deberá fabricar para maximizar sus ganancias?
(c)*¿Cuántos lotes tendría que fabricar para maximizar el número total de lotes?
RESOLUCIÓN apartado (a)
DETERMINACIÓN DE INCÓGNITAS
x ≡ "Número de lotes de tapas"
y ≡ "Número de lotes de envases"
CONJUNTO DE RESTRICCIONES
Lotes de tapas
Lotes de envases
litros barniz
1
2
minutos horno
5
3
x + 2y ≤ 1000 → litros de barniz
5x + 3y ≤ 3000 → minutos horno
x + y ≤ 650 → lotes
x≥0
y≥0
LA REGIÓN FACTIBLE
Realizamos unas sencillas tablas de valores...
x + 2y = 1000
5x + 3y = 3000
x
y
x
y
0
500
0
1000
1000
0
600
0
x + y = 650
x
0
650
y
650
0
En la PAU tendremos que ir realizando la actividad con lápiz y papel, en un solo dibujo,
aunque en el aula podremos utilizar herramientas auxiliares como lo puede ser una calculadora
gráfica, en nuestro caso, la fx – CG20 de CASIO. Para una mejor comprensión por parte del
alumnado, vamos a mostrar, de forma pautada, las imágenes de cómo se va obteniendo la
región factible en cada momento.
El nombre de la función y la verificación de uno de los infinitos puntos del semiplano figuran,
en cada momento, a la derecha de los mismos.
x + 2y ≤ 1000
Punto (0, 0)
0 ≤ 1000
SÍ se verifica
(0, 0) ∈ semiplano correspondiente
 Abel Martín
136
Del aula a la PAU
5x + 3y ≤ 3000
(0, 0)
0 ≤ 3000
SÍ se verifica
(0, 0) ∈ semiplano correspondiente
x + y ≤ 650
(0, 0)
0 ≤ 650
SÍ se verifica
(0, 0) ∈ semiplano correspondiente
x≥0
Todos los valores del primero y cuarto
cuadrantes
y≥0
Todos los valores del primero y segundo
cuadrantes
Finalmente podremos observar la solución del sistema de inecuaciones en forma de zona
sombreada, los vértices y los nombres de las rectas.
Las distintas combinaciones de lotes vienen representadas por los puntos (x, y)
pertenecientes a la región factible (sombreada), donde "x" es número de lotes de tapas e
"y" es el número de lotes de envases, con la condición de que tanto "x" como "y" sean
números naturales.
• ¿Se cumplirían los requisitos si la empresa fabricase 200 lotes de tapas y 100 lotes de
envases?
Sí es posible pues esa combinación viene representada por el punto (200, 100) y se
encuentra claramente dentro de la región factible.
RESOLUCIÓN apartado (b)
• Si la empresa vende todo lo que fabrica y gana por cada lote de tapas fabricado 3000 euros
y por cada lote de envases 4000 euros, ¿cuántos lotes de cada tipo deberá fabricar para
maximizar sus ganancias?
G(x, y) = 3000x + 4000y
 Abel Martín
La programación lineal
137
LOCALIZACIÓN DE SOLUCIONES
Teorema fundamental de la programación lineal: Como la región factible existe y está
acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono
que limita la región, o a lo largo de uno de los lados.
Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono
que constituye la región factible:
CÁLCULO DE VÉRTICES
A → Visualización directa en la gráfica y tabla de valores: A(0, 0)
B → Visualización directa en la gráfica y tabla de valores: B(0, 500)
C(x, y) Resolvemos el sistema
( −1)
(1)
x + y = 650 

x + 2 y = 1000
→
− x − y = −650
 → y = 350
x + 2 y = 1000 
x + 350 = 650
x = 300
x = 300 → y = 350
C(300,350)
D(x, y) Resolvemos el sistema
( −3)
x + y = 650 

(1) 5x + 3y = 3000
→
− 3x − 3y = −1950

5x + 3y = 3000 
→ 2x = 1050 →
x = 525
525 + y = 650
y = 125
x = 525 → y = 125 →
D(525, 125)
E → Visualización directa en la gráfica y tabla de valores: E(600, 0)
LA FUNCIÓN OBJETIVO
G(x, y) = 3000x + 4000y
ANÁLISIS DE ÓPTIMOS
Aplicamos el TEOREMA mencionado:
Vértices
A(0, 0)
B(0, 500)
C(300,350)
D(525, 125)
E(600, 0)
G(x, y) = 3000x + 4000y
3000·0 + 4000·0 =
3000·0 + 4000·500 =
3000·300 + 4000·350 =
3000·525 + 4000·125 =
3000·600 + 4000·0 =
Valor
0
2 000 000
2 300 000
2 075 000
1 800 000
Para maximizar las ganancias tendrá que fabricar 300 lotes de tapas y 350 lotes de
envases, momento en el que dichas ganancias ascenderán a 2 300 000 euros.
RESOLUCIÓN apartado (c)*
¿Cuántos lotes tendría que fabricar para maximizar el número total de lotes?
LA FUNCIÓN OBJETIVO
T(x, y) = x + y
ANÁLISIS DE ÓPTIMOS
Aplicamos el TEOREMA mencionado:
 Abel Martín
Del aula a la PAU
138
Vértices
A(0, 0)
B(0, 500)
C(300,350)
D(525, 125)
E(600, 0)
T(x, y) = x + y
0+0=
0 + 500 =
300 + 350 =
525 + 125 =
600 + 0 =
Valor
0
500
650
650
600
Tiene solución múltiple. Todas aquellas determinadas por los puntos (x, y) que se
encuentran sobre el segmento CD, donde C(300, 350) y D(525, 125), momentos en los
que el número de lotes total es de 650. Hay que tener en cuenta que en esos puntos (x, y)
deben verificar que x∈ Z+ , y∈ Z+
Criterios de corrección y calificación especificados en la prueba oficial:
(a) Plantear las inecuaciones: 0.75 puntos. Representar la región factible: 0.75 puntos. Cuestión:
0.25 puntos. (b) 0.75 puntos.
 Abel Martín