Ondas elásticas en sólidos - Departamento de Ciencia de Materiales
Anuncio

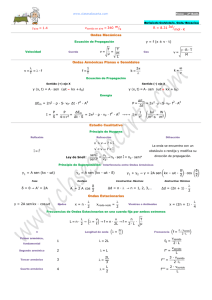
PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en sólidos Vicente Sánchez Gálvez Francisco Gálvez Díaz-Rubio David Cendón Franco http://www.mater.upm.es/Docencia/Master/PropiedadesDinamicas/Info.asp PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en sólidos CONTENIDO: – Introducción – Ondas en 1 dimensión – Ondas armónicas – Reflexión y propagación de ondas – Representación de ondas 2 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas • Onda: Perturbación que se propaga en el espacio – Acústicas, eléctrica, electromagnéticas … – Presión, tensión, deformación… • Ondas de tensión: • • • σ<σy, Elásticas σ>σy, Elasto-plásticas (deformaciones permanentes) Tipos: – Transversales – Longitudinales 3 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión • • • Medio semi-infinito unidimensional Medio Isótropo Régimen elástico σ S u = desplazamiento partículas σ = tensión S = sección u σ + dσ dx (σ + dσ ) S − σ S = dm ⋅ a ·· S ⋅ dσ = ( ρ ⋅ S ⋅ dx ) ⋅ u ∂σ ∂ 2u =ρ 2 ∂x ∂t 4 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión ∂σ ∂ 2u =ρ 2 ∂x ∂t σ = Φε ε= ∂ 2u ∂ 2u Φ 2 =ρ 2 ∂x ∂t ∂ 2u 1 ∂ 2u = ∂x 2 c 2 ∂t 2 c= Φ ρ ∂u ∂x Tensión uniaxial Deformación uniaxial Φ=E Φ = (λ + 2 μ ) c= E ρ λ + 2μ c= ρ νE λ= (1 + ν )(1 − 2ν ) μ= E 2(1 + ν ) 5 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión Desplazamientos ∂ 2u 1 ∂ 2u = ∂x 2 c 2 ∂t 2 La solución general es: u ( x, t ) = f ( x − ct ) + g ( x + ct ) u c= Φ ρ x La función de desplazamientos f representa una onda que se mueve en sentido positivo del eje x La función de desplazamientos g representa una onda que se mueve en sentido negativo del eje x 6 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión Tensiones, deformaciones y velocidades u ( x, t ) = f ( x − ct ) + g ( x + ct ) ε ( x, t ) = ∂ u ( x, t ) ∂ x ε ( x, t ) = f ′( x − ct ) + g ′( x + ct ) σ ( x, t ) = Eε ( x, t ) σ ( x, t ) = E [ f ′( x − ct ) + g ′( x + ct )] ∂ u ( x, t ) ∂t v( x, t ) = −cf ′( x − ct ) + cg ′( x + ct ) v ( x, t ) = 7 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión Relación entre Tensiones y Velocidades σ ( x, t ) = E [ f ′( x − ct ) + g ′( x + ct )] v( x, t ) = −cf ′( x − ct ) + cg ′( x + ct ) Teniendo en cuenta las expresiones de tensión y velocidad, se cumple que: σ = ± ρcv Si solo hay f : σ = − ρcv La onda se mueve en dirección positiva del eje x (c es positivo). Entonces: v tiene el mismo signo que c. La onda es de compresión, σ es negativo. v tiene el distinto signo que c. La onda es de tracción σ es positivo. Si solo hay g : σ = ρ cv Lo contrario 8 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas elásticas en 1 dimensión • Ejemplo de onda longitudinal en 1D v tracción c σ = − ρcv 9 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Ondas armónicas Aquellas en las que las funciones f y g son sinusoidales u ( x, t ) = f ( x − ct ) + g ( x + ct ) u ( x, t ) = A sin[k ( x − ct ) + ϕ ] + B sin[k ( x + ct ) + ψ ] u ( x, t ) = A sin(kx − ωt + ϕ ) + B sin(kx + ωt + ψ ) kc = ω kλ = 2π ωT = 2π ⇒ ⇒ c= λ= T= ω k 2π k 2π ⇒ c= λ T ω u ( x, t ) = A exp[i (kx − ωt )] + B exp[i (kx + ωt )] u ( x, t ) = A exp[ik ( x − ct )] + B exp[ik ( x + ct )] 10 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Cuando una onda al propagarse encuentra una perturbación o cambia de medio, se divide en dos: Onda trasmitida y onda reflejada u ( x, t ) = f ( x − ct ) x=0 Φ1 ρ1 Φ2 ρ2 c1 c2 u ( x, t ) = A exp[i (kx − ωt )] I R T uI ( x, t ) = AI exp ⎡⎣ik I ( x − c1t ) ⎤⎦ uT ( x, t ) = AT exp ⎡⎣ikT ( x − c2t ) ⎤⎦ uR ( x, t ) = AR exp ⎡⎣ik R ( x + c1t ) ⎤⎦ Condiciones en la interfase (x=0) para todo instante: u I + u R = uT uI x =0 + uR σ I + σ R = σT σI x =0 +σR x =0 x =0 = uT x =0 = σT x =0 11 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Primera condición: desplazamientos en x=0. uI x =0 + uR x =0 = uT x =0 AI exp ⎡⎣ik I ( 0 − c1t ) ⎤⎦ + AR exp ⎡⎣ik R ( 0 + c1t ) ⎤⎦ = AT exp ⎡⎣ikT ( 0 − c2t ) ⎤⎦ AI exp [ −ik I c1t ] + AR exp [ik R c1t ] = AT exp [ −ikT c2t ] Y ha de cumplirse para todo instante, luego: [ −ikI c1t ] = [ikR c1t ] [ −ikI c1t ] = [ −ikT c2t ] k R = −kI kT = k I c1 c2 AI + AR = AT 12 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Primera condición: tensiones en x=0. σI x =0 +σR x =0 = σT x =0 (− ρ1c1vI ) + (ρ1c1vR ) = (− ρ 2c2vT ) − ρ1c1 ∂u I ∂u ∂u + ρ1c1 R = − ρ 2 c2 T ∂t ∂t ∂t − ρ1c1 (−k I c1 AI ) + ρ1c1 (k R c1 AR ) = − ρ 2 c2 (− kT c2 AT ) AI − AR = kc ρ c k AI − ρ c k AR = ρ c I 1 AT c2 2 1 1 I 2 1 1 I 2 2 2 Se define la impedancia de un medio como: Y llamando R= Z2 Z1 Resulta: ρ 2 c2 A ρ1c1 T Z=ρc AI − AR = R AT 13 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Resumiendo: u I + u R = uT AI + AR = AT σ I + σ R = σT AI − AR = R AT luego: AT = 2 AI 1+ R AR = 1− R AI 1+ R 14 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Y los desplazamientos quedan: uI = AI exp ⎡⎣ik ( x − c1t ) ⎤⎦ uT = uR = uT 2 = uI 1 + R ⎡ c ⎤ 2 AI exp ⎢ik 1 ( x − c2t ) ⎥ 1+ R ⎣ c2 ⎦ uR uI 1− R AI exp ⎡⎣ −ik ( x + c1t ) ⎤⎦ 1+ R = 1− R 1+ R Y las tensiones quedan: σ I = σ max exp[ik ( x − c1t )] ⎡ c ⎤ 2R σT = σ max exp ⎢ik 1 ( x − c2t )⎥ 1+ R ⎣ c2 ⎦ σR = − 1− R σ max exp[− ik ( x + c1t )] 1+ R σ max = ρ1c12 kAI σT 2R = σ I 1+ R σR 1− R =− σI 1+ R 15 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Casos particulares a) Z2 > Z1 Z1 = ρ1c1 R>1 desplazamientos tensiones Amplitud onda reflejada − AI < uR < 0 0 < σR <σI Amplitud onda trasmitida 0 < uT < AI σ I < σ T < 2σ I Consecuencias: TENSIONES: • Una onda de compresión se refleja como compresión de menor valor • (id. en tracciones) Z 2 = ρ 2 c2 uT 2 = uI 1 + R uR uI = 1− R 1+ R σT 2R = σ I 1+ R σR 1− R =− σI 1+ R • Una onda de compresión se trasmite como compresión de mayor valor (entre 1 y 2 veces) • (id. en tracciones) Z1 = ρ1c1 Z 2 = ρ 2 c2 16 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Casos particulares b) Z2 < Z1 Z1 = ρ1c1 R<1 desplazamientos tensiones Amplitud onda reflejada 0 < uR < AI −σI < σR < 0 Amplitud onda trasmitida AI < uT < 2 AI 0 < σT < σ I Consecuencias: TENSIONES: • Una onda de compresión se refleja como tracción de menor valor absoluto • (y viceversa) Z 2 = ρ 2 c2 uT 2 = uI 1 + R uR uI = 1− R 1+ R σT 2R = σ I 1+ R σR 1− R =− σI 1+ R • Una onda de compresión se trasmite como compresión de menor valor absoluto • (id. en tracciones) Z1 = ρ1c1 Z 2 = ρ 2 c2 17 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Casos extremos Z1 = ρ1c1 a) Impedancias iguales uT = u I Z1 = Z 2 Z 2 = ρ 2 c2 uT 2 = uI 1 + R uR = 0 uR ⇒ R =1 uI σT = σ I σR = 0 = 1− R 1+ R σT 2R = σ I 1+ R σR 1− R =− σI 1+ R No hay onda reflejada La onda trasmitida es igual que la incidente Es como si no hubiera un cambio de medio. Z1 = ρ1c1 Z 2 = ρ 2 c2 18 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Z 2 = ρ 2c2 = ∞ Casos extremos Z1 = ρ1c1 a) Extremo fijo uT 2 = uI 1 + R uT = 0 Z 2 >> Z1 ⇒ R → ∞ uR = − uI uR uI σ T = 2σ I σR = σI = 1− R 1+ R σT 2R = σ I 1+ R σR 1− R =− σI 1+ R La tensión de la onda reflejada es igual que la incidente El desplazamiento cambia de sentido. Rebote Z2 = ∞ Z1 = ρ1c1 19 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas Z 2 = ρ 2 c2 = 0 Casos extremos Z1 = ρ1c1 3) Extremo libre uT 2 = uI 1 + R uT = 2 u I Z 2 << Z1 ⇒ R = 0 σT = 0 uR = uI uR uI = 1− R 1+ R σT 2R = σ I 1+ R σ R = −σ I σR 1− R =− σI 1+ R La tensión de la onda reflejada es igual que la incidente y de signo contrario El desplazamiento no cambia Z2 = 0 Z1 = ρ1c1 20 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas • Diagrama de Lagrange c1 x 1 c1 1 1 c2 c1 t 21 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas • Diagrama de Lagrange: Posición de las ondas en un instante c1 x t = t1 t 22 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas • Diagrama de Lagrange: Posición de las ondas en un instante c1 c2 Z2 < Z1 x t = t2 t 23 PROPIEDADES DINÁMICAS DE MATERIALES Universidad Politécnica de Madrid Departamento de Ciencia de Materiales Reflexión y propagación de ondas • Diagrama de Lagrange: Medida de las ondas en una posición x σ t = t2 t t 24