Septiembre - Universidad Autónoma de Madrid

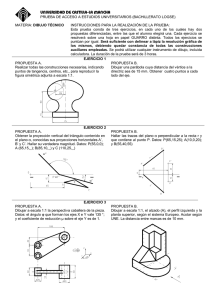
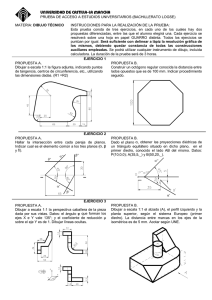
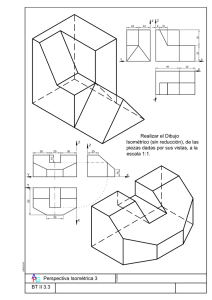
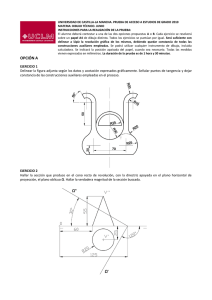
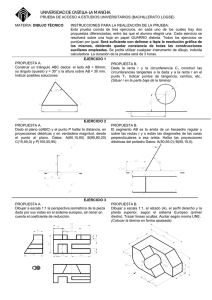
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS
OFICIALES DE GRADO
Curso 2010-2011
4
MATERIA: DIBUJO TÉCNICO II
INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
La prueba consiste en la resolución gráfica de los ejercicios de una de las dos opciones que se ofrecen: A o B.
Los ejercicios se pueden delinear a lápiz, debiendo dejarse todas las construcciones que sean necesarias.
La explicación razonada (justificando las construcciones) deberá realizarse, cuando se pida, junto a la resolución
gráfica. Cada ejercicio se valorará sobre 2,5 puntos. TIEMPO: Una hora y treinta minutos
OPCIÓN A
A1.- De un triángulo rectángulo se conoce la hipotenusa BC, y el punto de corte P sobre la misma de la
bisectriz del ángulo A.
B
C
P
A2.- Determinar el punto de la recta r más próximo al punto A, así como el segmento que definen.
Justificación razonada.
A2
r2
A1
r1
1
A3.- Las rectas VA, VB, VC, definen las direcciones de las aristas de una pirámide de vértice V, con base en
el plano Oxy y la cara VAC paralela al plano Oxz. Dibujar dicha pirámide.
z
V≡ V3
B2
B
O
A
C≡C1≡V1
x
y
A4.- Dibujar el corte AA de la pieza en la posición que corresponda.
A
A
2
OPCIÓN B
B1.- Hallar los puntos desde los cuales se pueden trazar segmentos tangentes de longitud 35 mm a ambas
circunferencias.
C1
C2
B2.- La figura ABCD se encuentra en un plano β. Del plano se conoce su traza horizontal β1 y la traza
vertical abatida (β0) sobre el plano horizontal. Hallar la verdadera magnitud de la figura.
A1
D1
B1≡ (B0)
C1
(β0)
β1
3
B3- Un plano contiene a la recta AB y secciona al prisma dado según un trapecio cuya base menor mide 3
cm. Representar la sección en dibujo isométrico.
Z
A
B
A
X
Y
B
B4.- Obtener las mínimas vistas diédricas necesarias de la pieza representada en dibujo isométrico.
4
DIBUJO TÉCNICO II
SOLUCIONES
OPCIÓN A
A1.- De un triángulo rectángulo se conoce la hipotenusa BC, y el punto de corte P sobre la misma de la
bisectriz del ángulo A. Dibujar dicho triángulo.
A
45º
B
C
P
45º
A2.- Determinar, el punto de la recta r más próximo al punto A, así como el segmento que definen.
Justificación razonada.
α2
A2
r2
P2
s2
P1
A1
s1
r1
α1
5
A3.- Las rectas VA, VB, VC, definen las direcciones de las aristas de una pirámide de vértice V, con base en
el plano Oxy y la cara VAC paralela al plano Oxz. Dibujar dicha pirámide.
z
V2
V≡ V3
B2
B
O
A
C≡C1≡V1
x
y
A4.- Dibujar el corte AA de la pieza en la posición que corresponda.
A
A
6
OPCIÓN B
B1.- Hallar los puntos desde los cuales se pueden trazar segmentos tangentes de longitud 35 mm a ambas
circunferencias.
P1
C1
C2
35 mm
P2
35 mm
B2.- La figura ABCD se encuentra en un plano β. Del plano se conoce su traza horizontal β1 y la traza
vertical abatida (β0) sobre el plano horizontal. Hallar la verdadera magnitud de la figura.
A1
D1
B1≡ (B0)
(A0)
C1
(β0)
(C0)
(D0)
7
β1
B3- Un plano contiene a la recta AB y secciona al prisma dado según un trapecio cuya base menor mide 3
cm. Representar la sección en dibujo isométrico.
Z
A
B
3,0
3,0
A
X
Y
B
B4.- Obtener las mínimas vistas diédricas necesarias de la pieza representada en dibujo isométrico.
8