Introducción: Formato de Complemento a 1:

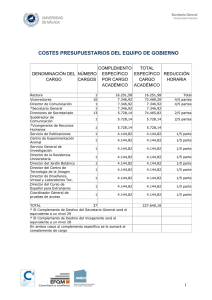
FORMATO BINARIO DE
NÚMEROS NEGATIVOS
Introducción:
Como sabemos, con un número n determinado de bits se pueden manejar 2 n números binarios distintos.
Hasta ahora hemos trabajado con números binarios puros, es decir, números naturales (positivos) y esto
nos permite el rango desde el 0 hasta el 2n-1. En el caso concreto de 8 bits, sabemos que se puede ir
desde el 0 hasta el 255, que son el 00000000b y el 11111111b, respectivamente.
Pues bien, si queremos representar números negativos, existen varias posibilidades:
• Formato de Coma Fija con Signo.
• Formato de Complemento a 1.
• Formato de Complemento a 2.
Todas las representaciones anteriores tienen en común que utilizan el primer bit como signo, de forma
que si ese bit es 0, se trata de un número positivo, y su representación es la que conocemos hasta ahora;
si el bit del signo es 1, se trata de un número negativo.
El sistema que utiliza internamente el ordenador para trabajar con números enteros es el formato de
Complemento a 2, pero vamos a ver también el formato de Complemento a 1, para introducirlo.
El formato de Coma Fija con Signo, simplemente mencionar que representa los números negativos
utilizando el bit de signo junto con los bits del número positivo correspondiente, pero esto no es de
utilidad para que el ordenador realice ningún cálculo. Vemos unos ejemplos:
64 = 0100.0000 b
82 = 0101.0010 b
-95 = 1101.1111 b
-49 = 1011.0001 b
Formato de Complemento a 1:
El primer sistema que se puede utilizar para realizar operaciones con números positivos y negativos de
forma sencilla por el ordenador es el Complemento a 1. Con este formato, el primer bit contiene el signo
y el resto contienen el complemento a 1 del valor absoluto (positivo) del número a representar.
El complemento a 1 de un número se obtiene cambiando 1's por 0's, y viceversa.
Los números positivos no cambian, pero los negativos sí.
El único inconveniente de este sistema es que el cero tiene dos representaciones, +0 y -0:
+0:
0000.0000 b
- 0:
1111.1111 b
El rango númerico con 8 bits abarca del -127 al 127 (en total 255 combinaciones, el cero es doble).
Así, los números del ejemplo anterior se representan de la siguiente manera:
64 = 0100.0000 b
82 = 0101.0010 b
95 = 0101.1111 b >>>>>> -95 = 1010.0000 b
49 = 0011.0001 b >>>>>> -49 = 1100.1110 b
La ventaja de este sistema es que las sumas y restas se hacen de forma binaria como hemos hecho hasta
ahora, sin considerar de forma especial el primer bit del signo. La única peculiaridad es que si la suma
tiene llevada en el bit de mayor peso (el de la izquierda) esa llevada se suma al resultado. Cuando
obtengamos el resultado, estará expresado en formato de Complemento a 1, es decir, si tiene signo
negativo, hay que cambiar 1's por 0's, y 0's por 1's para obtener el valor correspondiente.
Como ejemplo vamos a realizar los siguientes ejercicios, en formato de complemento a 1:
•
•
120 – 100
115 – 126
•
•
5 – 37
37 – 5
•
127 – 127
Ejercicio 1: Realizamos 120 – 100 = 120 + (-100)
Calculamos 120 y -100 en complemento a 1:
120 = 0111.1000 b
100 = 0110.0100 b >>>>> -100 = 1001.1011 b
Sumamos:
0111.1000 b
1001.1011 b
1 0001.0011 b (Se suma el rebose)
0001.0011 b
1b
Resultado: 0001.0100 b = 20
Ejercicio 2: Realizamos 115 – 126 = 115 + (-126)
Calculamos 115 y -126 en complemento a 1:
115 = 0111.0011 b
126 = 0111.1110 b >>>>> -126 = 1000.0001 b
Sumamos:
0111.0011 b
1000.0001 b
1111.0100 b
No hay rebose, pero es negativo: debemos obtener su valor por el complemento a 1:
1111.0100 b > > > > 0000.1011 b = 11
Resultado: 1111.0100 b = - 11
Ejercicio 3: Realizamos 5 – 37 = 5 + (-37)
Calculamos 5 y -37 en complemento a 1:
5 = 0000.0101 b
37 = 0010.0101 b >>>>>> -37 = 1101.1010 b
Sumamos:
0000.0101 b
1101.1010 b
1101.1111 b
No hay rebose, pero es negativo: debemos obtener su valor por el complemento a 1:
1101.1111 b > > > > 0010.0000 b = 32
Resultado: 1101.1111 b = - 32
Ejercicio 4: Realizamos 37 – 5 = 37 + (-5)
Calculamos 37 y -5 en complemento a 1:
37 = 0010.0101 b
5 = 0000.0101 b >>>>>>> -5 =
1111.1010 b
Sumamos:
0010.0101 b
1111.1010 b
1 0001.1111 b (Se suma el rebose)
0001.1111 b
1b
Resultado: 0010.0000 b = 32
Ejercicio 5: Realizamos 127 – 127 = 127 + (-127)
Calculamos 127 y -127 en complemento a 1:
127 = 0111.1111 b >>>>> -127 = 1000.0000 b
Sumamos:
0111.1111 b
1000.0000 b
1111.1111 b
No hay rebose, pero es negativo: debemos obtener su valor por el complemento a 1:
1111.1111 b > > > > 0000.0000 b = 0
Resultado: 1111.1111 b = - 0
Formato de Complemento a 2:
Con el formato binario de complemento a 1 se mejora con el complemento a 2. Con este sistema el cero
tiene una representación única, y se sigue manteniendo que el primer bit contiene el signo, mientras
que el resto contienen directamente el número (si es positivo) o el complemento a 2 del valor absoluto
el número.
El complemento a 2 de un número se obtiene sumando 1 al complemento a 1.
En este caso, el rango númerico con 8 bits va desde el -128 al 127 (256 combinaciones).
Los números utilizados en el ejemplo del complemento a 1 tienen esta representación:
64 = 0100.0000 b
82 = 0101.0010 b
95 = 0101.1111 b
(Comp. 1)
-95 = 1010.0000 b
(Comp. 2)
-95 = 1010.0001 b
49 = 0011.0001 b
(Comp. 1)
-49 = 1100.1110 b
(Comp. 1)
-49 = 1100.1111 b
Este sistema, además de utilizar una representación única para el cero, tiene la ventaja que no hay que
hacer nada con la llevada o acarreo del bit de mayor peso. Y se actúa de la misma forma que en el
complemento a 1: si el resultado es positivo, representa el número tal cual; si el resultado es negativo, se
calcula el complemento a 1 y se suma 1 para obtener el número positivo correspondiente.
Vamos a realizar los mismos ejemplos que hemos hecho con el complemento a 1 y verificaremos el
resultado para comprobar que es correcto.
Ejercicio 1: Realizamos 120 – 100 = 120 + (-100)
Calculamos 120 y -100 en complemento a 2:
120 = 0111.1000 b
Complemento a 1:
Complemento a 2:
100 = 0110.0100 b >>>>> -100 = 1001.1011 b >>>>> -100 = 1001.1100 b
Sumamos:
0111.1000 b
1001.1100 b
1 0001.0100 b (Se desecha el desbordamiento)
Resultado: 0001.0100 b = 20
Ejercicio 2: Realizamos 115 – 126 = 115 + (-126)
Calculamos 120 y -100 en complemento a 2:
115 = 0111.0011 b
Complemento a 1:
Complemento a 2:
126 = 0111.1110 b >>>>> -126 = 1000.0001 b >>>>> -120 = 1000.0010 b
Sumamos:
0111.0011 b
1000.0010 b
1111.0101 b (No hay desbordamiento, pero es negativo)
Complemento a 1:
Complemento a 2:
1111.0101 b >>>>> 0000.1010 b >>>>>> 0000.1011 b = 11
Resultado: 0001.0100 b = - 11
Ejercicio 3: Realizamos 37 – 5 = 37 + (-5)
Calculamos 37 y -5 en complemento a 2:
37 = 0010.0101 b
Complemento a 1:
Complemento a 2:
5 = 0000.0101 b >>>>>>> -5 = 1111.1010 b >>>>>>> -5 = 1111.1011 b
Sumamos:
0010.0101 b
1111.1011 b
1 0010.0000 b (Se desecha el desbordamiento)
Resultado: 0010.0000 b = 32
Ejercicio 4: Realizamos 5 – 37 = 5 + (-37)
Calculamos 5 y -37 en complemento a 2:
5 = 0000.0101 b
Complemento a 1:
Complemento a 2:
37 = 0010.0101 b >>>>>> -37 = 1101.1010 b >>>>>> -37 = 1101.1011 b
Sumamos:
0000.0101 b
1101.1011 b
1110.0000 b (No hay desbordamiento, pero es negativo)
Complemento a 1:
Complemento a 2:
1110.0000 b >>>>> 0001.1111 b >>>>>> 0010.0000 b = 32
Resultado: 1110.0000 b = - 32
Ejercicio 5: Realizamos 127 – 127 = 120 + (-127)
Calculamos 127 y -127 en complemento a 2:
127 = 0111.1111 b
Complemento a 1:
Complemento a 2:
127 = 0111.1111 b >>>>> -127 = 1000.0000 b >>>>> -127 = 1000.0001 b
Sumamos:
0111.1111 b
1000.0001 b
1 0000.0000 b (Se desecha el desbordamiento)
Resultado: 0000.0000 b = 0