ejercicios resueltos geometría en el plano

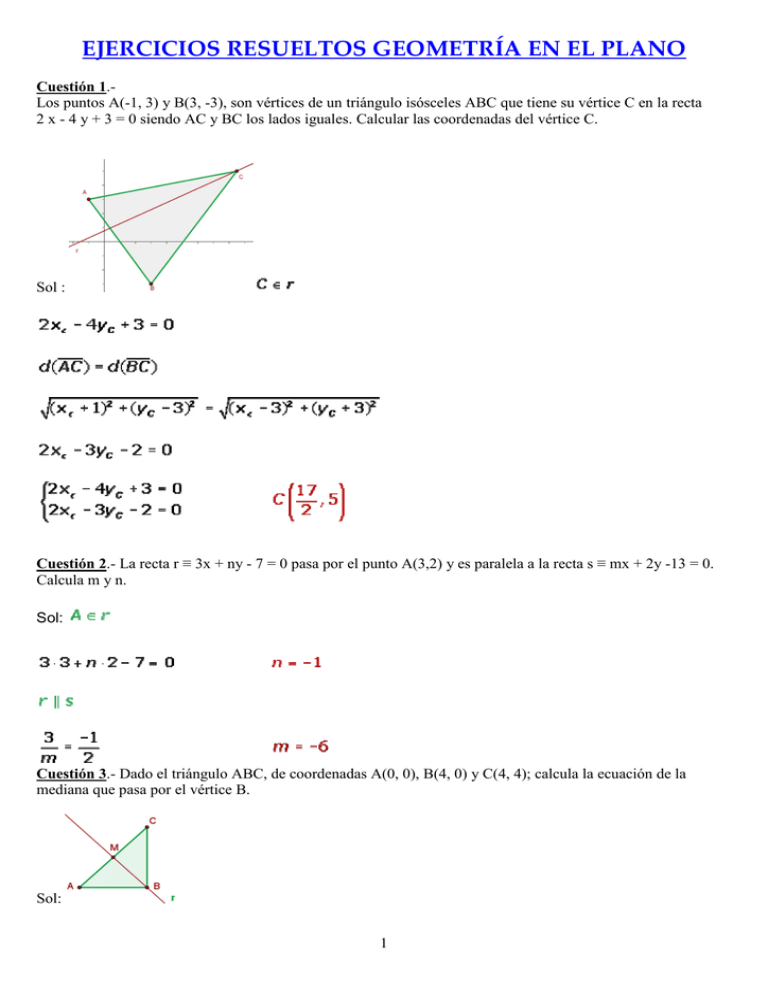
EJERCICIOS RESUELTOS GEOMETRÍA EN EL PLANO
Cuestión 1.Los puntos A(-1, 3) y B(3, -3), son vértices de un triángulo isósceles ABC que tiene su vértice C en la recta
2 x - 4 y + 3 = 0 siendo AC y BC los lados iguales. Calcular las coordenadas del vértice C.
Sol :
Cuestión 2.- La recta r ≡ 3x + ny - 7 = 0 pasa por el punto A(3,2) y es paralela a la recta s ≡ mx + 2y -13 = 0.
Calcula m y n.
Sol:
Cuestión 3.- Dado el triángulo ABC, de coordenadas A(0, 0), B(4, 0) y C(4, 4); calcula la ecuación de la
mediana que pasa por el vértice B.
Sol:
1
Cuestión 4.- Clasificar el triángulo determinado por los puntos: A(6, 0), B(3,0) y C(6, 3).
Sol:
Cuestión 5.- Se tiene el cuadrilátero ABCD cuyos vértices son A(3, 0), B(1, 4), C(-3, 2) y D(-1, -2).
Comprueba que es un paralelogramo y determina su centro.
2
Cuestión 6.- De un paralelogramo se conoce un vértice, A(8, 0), y el punto de corte de las dos diagonales, Q(6,
2). También sabemos que otro vértice se encuentra en el origen de coordenadas. Calcular:
1) Los otros vértices.
2) Las ecuaciones de las diagonales.
3) La longitud de las diagonales.
Sol:
1 Los otros vértices.
3
2 Las ecuaciones de las diagonales.
3 La longitud de las diagonales.
Cuestión 7.- Calcular las bisectrices de los ángulos determinados por la rectas:
Sol:
Cuestión 8.- Dadas las rectas r ≡ 3x + y - 1 = 0 y s ≡ 2 x + m y -8 = 0, determinar m para que formen un ángulo
de 45°
Sol:
4
Cuestión 9.- Dado el triángulo A(-1, -1), B(7, 5), C(2, 7); calcular las ecuaciones de las alturas y determinar el
ortocentro del triángulo.
Sol:
5
Cuestión 10.- Una recta es perpendicular a la que tiene por ecuación r ≡ 5x - 7y + 12 = 0 y dista 4 unidades del
origen. ¿Cuál es su ecuación?
Sol:
Cuestión 11.- Halla el punto simétrico A', del punto A (3, 2), respecto de la recta r ≡ 2x + y - 12 = 0.
Sol:
6
Cuestión 12.-
Cuestión 13.- Determinar el valor de a para que las rectas
r : 3ax - (a+1)y - 2(a+2) = 0 y s:(a+1)x - (a-1)y - (a+4) = 0 sean
1) paralelas
2) perpendiculares
5 ± 17
2) No tiene soluciones reales
4
Cuestión 14.- Hallar la distancia de A(-1,2) a la recta que corta a los ejes X e Y a las distancias 3 y 4 del
origen.
Sol: 1) a =
Sol: Hay 4 rectas solución 4x+3y-12=0, 4x-3y+12=0, -4x+3y+12=0 y –4x-3y-12=0
Cuestión 15.- Sea r la recta que pasa por el punto P(3, -2) y forma un ángulo de 45º con el eje OX positivo. Se
pide:
a) Un vector director y un vector normal de r
b) Las ecuaciones paramétricas y continua de r
 x = −1 + λ
c) La intersección, si la hubiera, con la recta s ≡ 
con λ ∈ R
 y = 2 − 2λ
d) La posición relativa de r y la recta t ≡ 10 x + 5 y − 3 = 0
e) El ángulo que forma r con el eje OY.
Cuestión 16.-
7
Cuestión 17.-
8
Cuestión 18.-
Cuestión 19.-
9
Cuestión 20.-
Cuestión 21.-
Cuestión 22.-
10
Cuestión 23.-
Cuestión 24.-
11
Cuestión 25.-
Cuestión 26.-
Cuestión 27.-
12
Cuestión 28.-
Cuestión 29.-
Cuestión 30.-
13
Cuestión 31.-
Cuestión 32.-
Cuestión 33.-
14
Cuestión 34.-
Cuestión 35.-
Cuestión 36.-
15
Cuestión 37.-
16
Cuestión 38.-
Cuestión 39.-
17
Cuestión 40.-
Cuestión 41.-
18
Cuestión 42.-
19
Cuestión 43.-
20
Cuestión 44.-
Cuestión 45.-
Cuestión 46.-
21
Cuestión 47.-
Cuestión 48.-
22
Cuestión 49.-
23
Cuestión 50.-
24