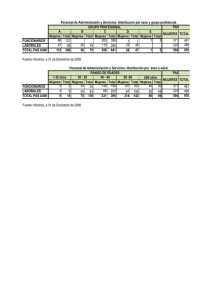
Se trata de eliminar un sobreespesor de 0.1 mm a la pieza de la

Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA: TECNOLOGÍAS DE FABRICACIÓN
Tiempo: 1 hora, 30 minutos
2.5 puntos
CURSO KURTSOA: 5º
NOMBRE IZENA:
FECHA DATA: 27.01.03
P1_FEB_03
Se trata de eliminar un sobreespesor de 0.1 mm a la pieza de la figura. La máquina es una rectificadora plana
de husillo horizontal y sus ejes positivos están representados sobre la pieza. La muela tiene 110 mm de
diámetro, 40 mm de anchura y gira a 7600 rpm. La pieza se mueve en vaiven en la dirección X a 5 m/min. La
profundidad en cada pasada se establece en 0.05 mm.
La operación se va a realizar de dos modos, en lo que se refiere al movimiento de avance transversal del
carro en la dirección Z. En el modo A, el carro se moverá 5 mm de golpe al final de cada doble carrera. En el
modo B el carro se moverá de manera continua con una velocidad tal que el caudal máximo neto sea igual al
máximo neto obtenido en el modo A.
Se pide:
1) Dibujar dos vistas en las que se represente la mesa, el carro, la pieza y la muela de la máquina a
emplear. Calcular el tiempo de operación en ambos modos (A, B) sabiendo que se tomarán creces de 5
mm a la entrada y a la salida tanto en X como en Z y que el tiempo de apagado de chispa se fija en 45
segundos. En la carrera de ida del modo A se elimina el 70% y en la de vuelta el 25%. En el modo B en
cada carrera se elimina un 70%. Calcular asimismo el avance máximo y la velocidad de avance en el eje
Z en el modo B.
2) Dibujar en perspectiva la huella producida por la herramienta en la pieza, en ambos modos, cuando la
herramienta se encuentra en medio de una carrera y marcar sobre ella la profundidad de pasada y el
avance transversal.
3) Durante el período de apagado de chispa el avance en Z se aumenta porque, en ausencia de profundidad
de pasada apreciable, el avance puede ser muy superior sin peligro para el proceso aunque lógicamente
no puede ser superior al ancho de la muela. Por otra parte el número de dobles carreras debe ser
necesariamente entero para evitar la marca que, en otro caso, dejaría la muela sobre la superficie de la
pieza. Durante el apagado de chispa y en ambos modos la velocidad de la mesa se mantiene igual que
durante el rectificado normal a 5 m/min.
Teniendo esto en cuenta, determinar el número de dobles carreras y el valor del avance en Z durante el
apagado de chispa en el modo A. Elegir el mínimo número de carreras posibles.
Determinar también el valor de la velocidad de avance en Z y el número de carreras en el modo B.
4) Determinar los caudales máximos durante el apagado de chispa en los modos A y B. .
Y
Z
X
180
80
1)
MUELA
aP
fZ
PIEZA
MESA X
Vx
MESA X
CARRO Z
⊗
CARRO Z
⊗ Vx
BANCADA
BANCADA
(1 punto)
Modo A
t opA = t 1pas ⋅ N pas + t ap = (t 1dc ⋅ N dc ) ⋅ N pas + t ap
t 1dc =
2 ⋅ (L X + 2∆ ) 2 ⋅ (180 + 2 ⋅ 5) mm
=
= 0.076 min
VX
5000 mm / min
N dc =
L Z + 2∆ + a m (80 + 2 ⋅ 5 + 40) mm
=
= 26 dc
fZ
5 mm / dc
N pas =
e
0.1 mm
=
=2
a P 0.05 mm
t opA = (0.076 ⋅ 26) ⋅ 2 + 0.75 = 3.952 + 0.75 = 4.702 min
Modo B
t opB = t 1pas ⋅ N pas + t ap =
(0.5 puntos)
L Z + 2∆ + a m
N pas + t ap
VZ
Cálculo de fZmáx
b
b
Z AWmáx = Z BWmáx → K AIDA ⋅ f ZA ⋅ a P ⋅ VX = K B ⋅ f Zmáx
⋅ a P ⋅ VX → f Zmáx
= f ZA = 5 mm
(0.5 puntos)
Cálculo de VZ
2
1
3
0
4
t 1−3 =
B
d1−3 f Zmáx
2 ⋅ (L X + ∆ )
=
=
VZ
VZ
VX
Despejando VZ, se obtiene:
B
f Zmáx
5 mm
mm
mm
VZ = VX
= 5000
= 67.57
2 ⋅ (L X + ∆ )
min 2 ⋅ (180 + 5) mm
min
t opB =
(0.5 puntos)
L Z + 2∆ + a m
(80 + 2 ⋅ 5 + 40) mm ⋅ 2 + 0.75 = 1.924 ⋅ 2 + 0.75 = 4.598 min
⋅ N pas + t ap =
mm
VZ
67.57
min
(0.5 puntos)
2)
Modo A
fZ
aP
(1 punto)
Modo B
fZmáx
fZ
aP
(1 punto)
3)
Modo A
t apA = 0.75 min = N pas ⋅ N dc ⋅ t 1dc
Suponiendo N pas = 1 y sabiendo que t 1dc = 0.076 min :
N dc =
0.75 min
= 9.87 dc
0.076 min/ dc
Tomando N dc = 10 dc ( N c = 20 c ) → f Z =
(80 + 2 ⋅ 5 + 40) mm = 13 mm
10 dc
(2 puntos)
Modo B
t apB = 0.75 min = N pas ⋅ N c ⋅ t 1c
Suponiendo N pas = 1 :
t 1c =
(L X + 2∆ ) = (180 + 2 ⋅ 5) mm = 0.038 min
Nc =
VX
5000 mm / min
0.75 min
= 19.74 carreras
0.038 min/ dc
Para 19 carreras, el número de dobles carreras Ndc=9.5 no es entero.
Por tanto, para 20 carreras, se toman 10 dc.
t apB = 0.75 min =
L Z + 2∆ + a m
130 mm
mm
→ VZ _ ap =
= 173.3
VZ _ ap
0.75 min
min
(2 puntos)
4)
Modo A
Z
A
Wmáx _ ap
 mm 3 
mm
= K ⋅ f Z _ ap ⋅ a P ⋅ VX = 0.05 ⋅13.7 mm ⋅ 0.05 mm ⋅ 5000
= 171.25 

min
 min 
A
ap
(0.5 puntos)
Modo B
t 1−3 =
Z
B
f Zmáx
_ ap
VZ _ ap
B
Wmáx _ ap
=
2 ⋅ (L X + ∆ )
2 ⋅ (L X + ∆ )
mm 2 ⋅ (180 + 5)
B
→ f Zmáx _ ap = VZ _ ap ⋅
= 173.3
⋅
= 12.824 mm
VX
min 5000 mm
VX
min
= K ⋅f
B
ap
B
Zmáx _ ap
 mm 3 
mm
⋅ a P ⋅ VX = 0.3 ⋅12.824 mm ⋅ 0.05 mm ⋅ 5000
= 961.8 

min
 min 
(0.5 puntos)