Tema: Constantes, Variables y Expresiones

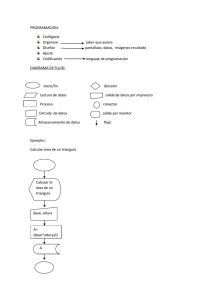
Tema: Constantes, Variables y Expresiones.
Objetivo: Los alumnos conocerán las características de Constantes, Variables y
Expresiones identificando su concordancia y discrepancia.
Constantes.
1
Es un objeto de valor invariable. Este valor no cambia durante el proceso, los tipos
de constantes mas comunes son:


Enteras o integer.

Reales o decimales.

De carácter y

Boleanas o lógicas.
Constante entera o integer : Es un numero con valor entero positivo o
negativo.

Constantes reales: Una constante real o decimal es un número escrito con
un punto decimal.

Constante de carácter: Es un conjunto de uno o varios caracteres,
normalmente los caracteres disponibles son letras mayúsculas, minúsculas,
dígitos, signos de puntuación y otros símbolos especiales.
Variables.
Es un objeto cuyo valor es variable (cambiante), toda variable posee dos atributos;
un nombre o identificador (que es invariable) y que sirve para designarla y un tipo
que describe la posible utilización de la variable.

Variables Enteras o Integer: Son variables que almacenan datos numéricos
enteros.

Variables reales: Son variables que almacenan datos numéricos decimales,
ya seas positivos o negativos.

Variables boleanas: Son variables que almacenan dos posibles datos, Falso
o Verdadero.

Variables de carácter: Son variables que almacenan cadenas de caracteres
ya sean Alfabéticos, numéricos, o caracteres especiales.
LIC. EDGAR DE LA CRUZ GARCÍA.
Expresiones.
Las expresiones son combinaciones de constantes, variables, símbolos de
operación, paréntesis y nombres de funciones especiales.
2
Símbolos de operación.
(+) Adición.
(*) Multiplicación.
( - ) Sustracción.
(/) División.
Operadores de relación o comparación.
( < ) Menor que...
( >= )Mayor o igual que...
( > ) Mayor que...
( = ) Igual que...
( <= ) Menor o igual que...
( <> ) Desigual que...
LIC. EDGAR DE LA CRUZ GARCÍA.
Tema: Diagramas de flujo.
Objetivo: Los alumnos analizarán y aplicarán (en ejercicios reales) los diagramas
de flujo.
Símbolos utilizados en los diagramas de flujo.
3
Nombre y función.
Símbolo.
Terminal (inicio y fin).- Representa el inicio y el
fin de un programa (diagrama de flujo).
Entrada/ salida.- Se utiliza para introducir datos
en la computadora, así también para representar
los datos de salida.
Proceso.- Se utiliza para representar cualquier
tipo de operación definida, que pueda originar
cambios de valor.
Decisión.- Indica operaciones lógicas o de
comparación entre datos con dos posibles
respuestas.
Decisión múltiple.- Indica operaciones lógicas o
de comparación entre datos con múltiples
salidas.
Conector.-
Sirve para enlazar dos partes
cualesquiera de un organigrama, siempre y
cuando se encuentren en la misma página.
Líneas
de
flujo.-
Indican
en
sentido de
ejecución de las operaciones.
Conector.- Sirve para conectar o enlazar dos
puntos del organigrama situado en dos paginas
diferentes.
LIC. EDGAR DE LA CRUZ GARCÍA.
Tema: Diagramas de flujo.
Objetivo: Los alumnos desarrollarán la habilidad para resolver problemas,
mediante diagramas de flujo.
Ejemplo: Diagrama de flujo.
4
Diagrama de flujo que calcula el área de un triangulo:
INICIO
DATOS DE
ENTRADA.
“TECLEA EL VALOR DE LA
BASE DEL TRIANGULO”, B
“TECLEA EL VALOR DE LA
ALTURA DEL TRIANGULO”, H
PROCESO.
DATOS DE
SALIDA.
A = ((B * H)/2)
“EL AREA TOTAL DEL
TRIANGULO ES ”, A
FIN
EJERCICIOS.
1.- Realiza un diagrama de flujo que calcule el volumen de una pirámide.
2.- Realizar un diagrama de flujo que pida la distancia en metros y los convierta a
milímetros, centímetros, decímetros, decámetros, hectómetros y kilómetros.
3.- Realizar un diagrama de flujo que calcule el área del triangulo y del rectángulo
y calcule la suma de las dos áreas.
4.- Realizar un diagrama de flujo que calcule el área de un cono.
5.- Realizar un diagrama de flujo que realice las cuatro operaciones básicas.
6.- ¿Qué relación tiene el saber organizar diagramas de flujo en la vida cotidiana?
LIC. EDGAR DE LA CRUZ GARCÍA.
Tema: Diagramas de flujo con decisión.
Objetivo: Los alumnos conocerán y desarrollarán la habilidad para resolver
problemas tomando en cuenta decisiones con instrucciones previamente
planteadas.
La instrucción de decisión es simplemente el razonamiento del resultado
esperado, mediante los aperadores de relación.
Ejemplo: Diagrama de flujo con la opción SI.
Diagrama de flujo que pida la edad en años, y determine si es mayor de edad o
no:
INICIO
“TECLEA TU EDAD EN AÑOS”,
E
E>=18
SI
“ERES MAYOR
DE EDAD”
FIN
NO
“ERES MENOR
DE EDAD”
FIN
EJERCICIOS.
1.- Realiza un diagrama de flujo que pida 10 calificaciones cualquiera, que calcule
el promedio y que imprima si esta aprobado o reprobado.
2.- Realizar un diagrama de flujo que pida un numero y determine si es positivo,
negativo o neutro.
3.- (Situación Real) Un trabajador gana $50.00 pesos la hora en las primeras 40
horas trabajadas, y $70.00 pesos cada hora extra, Realizar un diagrama de flujo
que calcule el sueldo del trabajador.
LIC. EDGAR DE LA CRUZ GARCÍA.
5
Tema: Funciones numéricas. (Aritméticas).
Objetivo: Los alumnos conocerán las funciones más comunes para la resolución
de ejercicios matemáticos.
6
ASB.- Devuelve el valor absoluto de una expresión numérica, su formado es:
ABS
Variable
.
Exp. Numérica.
SQR.- Devuelve la raíz cuadrada de una expresión numérica, la expresión debe
ser mayor de cero, la expresión es:
Variable = SQR (expresión numérica).
ATN.- Obtiene la acotangente de X, donde X está expresada en radianes. Su
formato es ATN (X) donde X es un número cualquiera.
CINT.- Redondea números como parte fraccionaria al siguiente numero completo
o entero. Su formato es CINT (X).
COS.- Calcula el coseno del rango de X y su formato es COS (X).
FIX.- Trunca X a un número entero su formato es FIX (X).
SIN.- Calcula en radianes la función trigonométrica del seno, su formato es SIN(X).
TAN.- Calcula la función trigonométrica de la tangente, su formato es TAN (X).
Ejercicio:
De cada función realiza un diagrama de flujo.
LIC. EDGAR DE LA CRUZ GARCÍA.
Tema: Seudocódigo.
Objetivo: Los alumnos aprenderán a llevar la estructura de un diagrama de flujo a
un seudocódigo.
Seudocódigo.
El seudocódigo es un algoritmo muy parecido a un lenguaje de programación
puesto que se utiliza la misma estructura.
Para realizar un seudocódigo se siguen los mismos que al realizar un diagrama de
flujo, es decir primero se realiza el problema, se determinan variables y todas las
posibles salidas.
Ejemplo:
Realiza un seudocódigo que calcule el área del triangulo.
Inicio:
Entrada “Teclea el Valor de la Base”, b
Entrada “Teclea el Valor de la Altura”,h
A=(b*h)/2
Salida “El área del triangulo es”, A
Fin.
Ejercicios.
1. Realizar una seudocódigo que convierta grados centígrados a grados
farenhey.
2. Programa que calcule las horas dormidas de una persona.
3. Programa que calcule el cuadrado de un numero.
4. Programa que pida el nombre de un cliente, fecha de compra, código del
cliente, cantidad comprada, precio unitario y que calcule la venta bruta,
monto del descuento de un 15% y la venta neta.
5.
Programa que obtenga el costo de venta y realice un descuento del 15% si
la venta es mayor de $50.00, de otro modo que realice un descuento del 10%
LIC. EDGAR DE LA CRUZ GARCÍA.
7