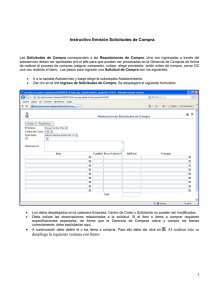
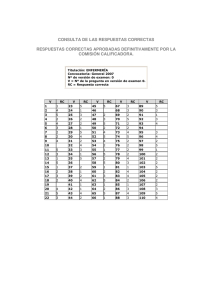
INFORME MATEMATICAS VF 23-2-2016

Créditos
Informe Curricular de Pruebas Nacionales 2015:
-
Ministerio de Educación de la Republica Dominicana
Vice Ministerio de Supervisión, Evaluación y Control de la Calidad
Elaboración:
-
Dirección General de Evaluación de la Calidad
Revisión:
-
Dirección General de Evaluación de la Calidad
Diseño y Diagramación:
-
German Peña Santos, Dirección de Evaluación de la calidad
Castulo Antonio Reyes Abreu, Dirección de Evaluación de la calidad
Bianca Gisselle Senior, Dirección de Evaluación de la calidad
Impresión:
Dirección de Evaluación de la Calidad
Departamento de Pruebas Nacionales
Área: Matemática
Equipo Técnico de Matemática
MARÍA ALTAGRACIA PÉREZ F.
VÍCTOR MANUEL ROSARIO A.
YANILE ALTAGRACIA VALENZUELA C.
GILBERTO RODRÍGUEZ M.
Santo Domingo, República Dominicana, Noviembre 2015
Índice de Contenidos
Introducción ............................................................................................................... 1
1.1
Comparación de las Pruebas Nacionales de Matemática, en 2014 y 2015 .............. 3
I. Octavo Grado .......................................................................................................... 4
1.1.
Puntaje Promedio en las Pruebas Nacionales de Matemática 2015........................ 4
1.2.
Porcentaje de respuestas correctas e incorrectas por dominios ............................ 4
1.3. Descripción de los ítems que resultaron fáciles y los que resultaron difíciles en las
Pruebas Nacionales de Matemática de Octavo Grado. .............................................. 7
1.4.
Análisis de Algunos ítems de las Pruebas Nacionales ............................................ 8
1.5.
Contenidos de mayor dificultad de acuerdo a errores cometidos en los ítems ..... 12
II. Tercer Ciclo de Adultos ....................................................................................... 14
2.1.
Puntaje Promedio en Las Pruebas Nacionales de Matemática 2015 ..................... 14
2.2.
Porcentajes de respuestas correctas e incorrectas por dominios ......................... 14
2.3. Descripción de los ítems que resultaron fáciles y los que resultaron difíciles en las
Pruebas de Matemática en Tercer Ciclo de Adultos. .............................................. 17
2.4.
Análisis de los ítems que resultaron más fáciles y más difíciles ........................... 18
2.5.
Contenidos de mayor dificultad de acuerdo a errores cometidos en los ítems ..... 22
III. Nivel Medio Modalidad General ......................................................................... 23
3.1.
Puntaje Promedio en Pruebas Nacionales de Matemáticas 2015 ......................... 23
3.2.
Porcentajes de respuestas correctas e incorrectas por dominios ......................... 23
3.3. Descripción de los ítems que resultaron fáciles y los que resultaron difíciles en las
Pruebas Nacionales de Matemática del Nivel Medio Modalidad General. ................ 26
3.4.
Análisis de los ítems que resultaron más fáciles y más difíciles ........................... 28
3.5.
Contenidos de mayor dificultad de acuerdo a errores cometidos en los ítems ..... 33
IV. Nivel Medio: Modalidad Técnico Profesional y Artes. ..................................... 35
4.1.
Puntaje Promedio en Las Pruebas Nacionales de Matemática 2015..................... 35
4.2.
Porcentajes de respuestas correctas e incorrectas por dominios ......................... 35
4.3. Descripción de los ítems que resultaron fáciles y los que resultaron difíciles en las
Pruebas Nacionales de Matemática en Media Técnico- Profesional y Artes............. 38
4.4.
Análisis de los ítems que resultaron más fáciles y más difíciles ........................... 40
4.5.
Contenidos de mayor dificultad de acuerdo a errores cometidos en los ítems ..... 43
Conclusión ............................................................................................................... 46
Anexos ...................................................................................................................... 48
Índice de tablas
Tabla No.1 ................................................................................................................... 3
Resultados Pruebas Nacionales de Matemática por nivel, convocatoria y año. .......... 3
Tabla No. 1.1 ............................................................................................................... 4
Promedio de puntajes y total de estudiantes examinados en las Pruebas Nacionales
de Matemática, por convocatoria en Octavo Grado Nivel Básico 2015 ....................... 4
Tabla No. 1.2 ............................................................................................................... 5
Composición de la prueba de Matemática y promedios de porcentajes de respuestas
correctas e incorrectas en ambas convocatorias de las Pruebas Nacionales de
Octavo Grado del Nivel Básico .................................................................................... 5
Tabla No. 1.3 ............................................................................................................... 6
Composición de la prueba de Matemática y porcentaje de respuestas correctas por
dominios y por nivel de complejidad en ambas convocatorias de Octavo Grado Nivel
Básico 2015 ................................................................................................................. 6
Tabla No. 2.1. ............................................................................................................ 14
Promedio de puntajes y total de estudiantes examinados por convocatoria en las
Pruebas Nacionales de Matemática 2015, en el Tercer Ciclo de Adultos del Nivel
Básico. ....................................................................................................................... 14
Tabla No. 2.2 ............................................................................................................. 15
Composición de la prueba de matemática y porcentajes de respuestas correctas e
incorrectas en ambas convocatorias de las Pruebas Nacionales 2015 en el Tercer
Ciclo de Adultos del Nivel Básico............................................................................... 15
Tabla No. 2.3 ............................................................................................................. 16
Composición de la prueba de matemática y porcentaje de respuestas correctas por
dominios y nivel de complejidad en ambas convocatorias, Tercer Ciclo de Adultos del
Nivel Básico 2015 ...................................................................................................... 16
Tabla No. 3.1 ............................................................................................................. 23
Promedio de puntaje y total de estudiantes examinados en la Prueba Nacional de
Matemática 2015, por Convocatoria en el Nivel Medio Modalidad General ............... 23
Tabla No. 3.2. ............................................................................................................ 24
Composición de la prueba de Matemática y promedios de porcentajes de respuestas
correctas e incorrectas en ambas convocatorias de las Pruebas Nacionales 2015 en
el Nivel Medio Modalidad General ............................................................................. 24
Tabla No. 3.3 ............................................................................................................. 25
Composición de la prueba de matemática y porcientos de respuestas correctas por
dominios y nivel de complejidad en ambas convocatorias 2015, Nivel Medio
Modalidad General..................................................................................................... 25
Tabla No. 4.1 ............................................................................................................. 35
Promedio de puntajes y total de estudiantes examinados en las Pruebas Nacionales
de Matemática, por Convocatoria en el Nivel Medio Modalidad Técnico Profesional y
Artes en el 2015 ......................................................................................................... 35
Tabla No. 4.2 ............................................................................................................. 36
Composición de la prueba de matemática y porcentajes de respuestas correctas e
incorrectas , en ambas convocatorias de las Pruebas Nacionales 2015, en el Nivel
Medio Modalidad Técnico-Profesional y Artes ........................................................... 36
Tabla No. 4.3 ............................................................................................................. 37
Composición de la prueba y porcientos de respuestas correctas por dominios y nivel
de complejidad en las Pruebas Nacionales de Matemática 2015, Nivel Medio
Modalidad Técnico-Profesional. ................................................................................. 37
Tabla Anexo No. 1 .................................................................................................... 48
Descripción de los niveles taxonómicos en los procesos cognitivos de Matemática . 48
Tabla Anexo No. 2 .................................................................................................... 49
Descripción de los dominios en Octavo Grado .......................................................... 49
Tabla Anexo No. 3 .................................................................................................... 49
Tabla de especificaciones para Octavo Grado .......................................................... 49
Tabla Anexo No. 4 .................................................................................................... 49
Descripción de los dominios en Tercer Ciclo de Adultos ........................................... 49
Tabla Anexo No. 5 .................................................................................................... 49
Tabla de especificaciones para Tercer Ciclo de Adultos ........................................... 49
Tabla Anexo No. 6 .................................................................................................... 49
Descripción de los dominios en Media Modalidad General ....................................... 49
Tabla Anexo No. 7 .................................................................................................... 49
Tabla de especificaciones para Media Modalidad General ........................................ 49
Tabla Anexo No. 8 .................................................................................................... 49
Descripción de los dominios en Media Modalidad Técnico Profesional y Artes ......... 49
Tabla Anexo No. 9 .................................................................................................... 49
Tabla de especificaciones para Media Modalidad Técnico Profesional y Artes ......... 49
Índice de Gráficos
Gráfico 1.1 .................................................................................................................. 5
Porcentajes de respuestas correctas e incorrectas, por dominio en la Primera y
Segunda Convocatoria de las Pruebas Nacionales 2015 de Matemática, Octavo
grado del Nivel Básico ................................................................................................. 5
Gráfico 2.1 ................................................................................................................ 15
Porcentajes de respuestas correctas e incorrectas por cada dominio en la Primera y
Segunda Convocatoria de las Pruebas Nacionales 2015 de Matemática, Tercer ciclo
de Adultos del Nivel Básico........................................................................................ 15
Gráfico 3.1 ................................................................................................................ 24
Porcentajes de respuestas correctas e incorrectas por cada uno de los dominios en
la Primera y Segunda Convocatoria de las Pruebas Nacionales 2015 de Matemática,
Nivel Medio, modalidad general ................................................................................. 24
Gráfico 4.1 ................................................................................................................ 36
Porcentajes de respuestas correctas e incorrectas por cada uno de los dominios en
la Primera y Segunda Convocatoria de las Pruebas Nacionales 2015 de Matemática,
nivel medio modalidad técnico-profesional ................................................................ 36
Introducción
Las Pruebas Nacionales son instrumentos que evalúan los aprendizajes logrados por los
estudiantes al concluir un nivel educativo, de acuerdo a lo establecido en el currículo oficial
vigente. Por tanto, su propósito fundamental es determinar la calidad de los logros de los
aprendizajes de los estudiantes al finalizar el Octavo Grado y el Tercer Ciclo de Adultos para el
Nivel Básico, así como también al finalizar el Nivel Medio en su Modalidad General, Técnico
Profesional y Artes. Sus resultados tienen un componente de certificación (30% de la
calificación final para promoción) y un componente diagnóstico que aporta información sobre el
desempeño del sistema educativo para tomar medidas que contribuyan a mejorar la calidad de
la educación.
Este informe presenta los resultados de las Pruebas Nacionales de Matemática 2015
destacando el desempeño de los estudiantes en relación al dominio de los contenidos
propuestos en el currículo. El propósito es ofrecer información sobre el desempeño curricular a
toda la comunidad educativa con el fin de que dicha información oriente la toma de decisiones
para enfrentar y superar las debilidades detectadas en el aprendizaje de los estudiantes.
De manera especial, este informe pretende propiciar la discusión, el análisis y la reflexión de
las autoridades, técnicos, directores, coordinadores y docentes de los centros educativos en
torno a los aprendizajes, al desarrollo del currículo y la práctica docente, y a la gestión
institucional y pedagógica, para motivar acciones, apoyos y planes que impulsen la mejora del
proceso de enseñanza-aprendizaje.
El diseño de las pruebas nacionales se elabora a partir del análisis del currículo que conlleva la
selección y distribución de los contenidos a evaluar y de los niveles taxonómicos (que son los
distintos grados de complejidad de los ítems) para cada grado, nivel o modalidad, lo cual se
recoge en la tabla de especificaciones del Marco Teórico-Conceptual de las Pruebas
1
Nacionales (2011) .
Para el diseño de las Pruebas Nacionales de Matemática, se toman en cuenta los propósitos
de cada grado o nivel y los ejes temáticos del área, que permiten desarrollar indicadores de
evaluación para los diferentes contenidos que presenta el currículo. Estos contenidos se
reorganizan en grandes categorías llamadas “dominios”. Los ítems o preguntas que conforman
la prueba se agrupan además en niveles taxonómicos según la complejidad de los procesos
cognitivos evaluados y en general se describen a continuación:
-
1
El marco teórico-conceptual de pruebas nacionales actualizado (2011) está disponible en la página web del
Ministerio de Educación. http://www.minerd.gob.do/sitios/pnacionales/SitePages/Home.aspx
1

Nivel 1: Se refiere a procesos que implican el conocimiento y la comprensión de hechos
y datos, recordar información, localizar un dato, definir un concepto, identificar
elementos.

Nivel 2: Se refiere a procesos que implican la comprensión de relaciones simples e
interacciones de varios elementos, la construcción de significados a partir de elementos
dados, el establecer conexiones.

Nivel 3: Se refiere a aplicar principios, resolver problemas, analizar múltiples elementos
que intervienen en una situación, sus relaciones e implicaciones.
(Para más detalles ver los anexos)
Este informe, primero presenta una comparación de los promedios de puntajes globales de los
años 2014 y 2015 en la primera y segunda convocatoria y luego se organiza en cuatro grandes
secciones: Octavo Grado, Tercer Ciclo de Adultos, Media General y Media Técnico profesional
y Artes. Cada sección contiene la siguiente información:
A) Puntaje promedio obtenido por los estudiantes tanto en la primera como en la segunda
convocatoria a nivel nacional.
B) Descripción de la composición de cada prueba en relación a lo que evalúa.
C) Porcentaje de respuestas correctas e incorrectas por dominios y niveles taxonómicos.
D) Análisis de ejemplos de ítems fáciles y difíciles así como de contenidos de mayor dificultad
o donde cometen errores con mayor frecuencia
E) Conclusiones y sugerencias.
Para interpretar las categorías de fácil y difícil se considera el parámetro de dificultad del ítem
según los análisis estadísticos aplicados a las Pruebas Nacionales. Se considera “fácil” un ítem
que lo contestó más del 74 % de la población, “aceptable” de 27-73 %, y “difícil” si lo contestó
menos de 27 % de la población examinada.
Con los resultados de las Pruebas Nacionales 2015, analizados así, se procura motivar al
lector a reflexionar sobre los factores que se relacionan con estos resultados y a buscar
posibles soluciones para mejorar aquellos contenidos y temas donde hay debilidades; de igual
modo, sostener aquellos de mayor dominio con el fin de elevar la calidad de la educación
dominicana.
Finalmente, el Equipo Técnico de Matemática de Pruebas Nacionales hace algunas
sugerencias y consideraciones didáctico-metodológicas donde se identifican los retos y
deficiencias más importantes para cada grado, modelado con ejemplos. El objetivo es que
estas recomendaciones aporten para mejorar los resultados de las Pruebas Nacionales, y con
ellos al sistema educativo dominicano.
2
1.1
Comparación de las Pruebas Nacionales de Matemática en 2014 y
2015
Tabla No.1
2
Año
Resultados Pruebas Nacionales de Matemática por nivel, convocatoria y
año.
Convocatorias Niveles
Básico
1
Medio
2014
Básico
2
Medio
Básico
1
Medio
2015
Básico
2
Medio
Grado y Modalidades
Presentes Promedios de Puntajes
Octavo Grado
150,688
15.01
Adultos
31,373
14.67
General
110,893
16.23
Técnico Profesional y Artes
18,141
17.2
Octavo Grado
29,475
14.23
Adultos
5,280
13.81
General
61,836
15.8
Técnico Profesional y Artes
7,480
15.43
Octavo Grado
151,095
15.29
Adultos
29,376
15.11
General
108,740
16.78
Técnico Profesional y Artes
18,585
17.53
Octavo Grado
26,088
14.21
Adultos
4,652
14.44
General
51,426
15.81
Técnico Profesional y Artes
6,429
16.21
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Los puntajes de las Pruebas Nacionales se presentan en una escala de 0-30, con una media
de la prueba establecida en 17 para la prueba de básica y 18 para la prueba del nivel medio y
una desviación estándar de 4 puntos.
Al observar los promedios de puntajes en un año en las dos convocatorias se observa que los
promedios de puntajes de la primera convocatoria son ligeramente superiores a los de la
segunda convocatoria. La segunda convocatoria presenta puntajes más bajos siempre. Aquí se
debe tener en cuenta que, en su mayoría, los estudiantes que acuden a una segunda
convocatoria, son aquellos que por diversos factores no completaron a tiempo las asignaturas
del centro educativo y tuvieron que ir a exámenes completivos o no pudieron aprobar en la
primera, y por tanto presentan debilidades en su desempeño académico.
Si se hace una comparación de los promedios de puntajes de la primera convocatoria de
ambos años como con la segunda, se observa un ligero incremento en los promedios de
puntajes en los grados y modalidades evaluados, a excepción de la segunda convocatoria de
Octavo Grado, que en el año 2015 bajó dos centésimas. En general, los resultados son
similares pero se puede apreciar un aumento en el puntaje de matemática en el 2015 con
relación al 2014, especialmente en la primera convocatoria que es a la que asiste la mayoría de
estudiantes. Monitorear los resultados de las Pruebas Nacionales a través del tiempo permite ir
identificando la tendencia en el rendimiento y verificar si se está progresando.
3
I. Octavo Grado
1.1. Puntaje Promedio en las Pruebas Nacionales de Matemática 2015
El promedio del puntaje obtenido por los estudiantes de Octavo Grado en ambas convocatorias
se muestra en la siguiente tabla
Promedio de puntajes y total de estudiantes examinados en las Pruebas
Nacionales de Matemática, por convocatoria en Octavo Grado Nivel
Básico 2015
Tabla No. 1.1
Octavo Grado
Convocatorias
Promedio de puntajes
Total de examinados
Primera
15.29
151,095
Segunda
14.21
26,088
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Siendo la puntuación de las Pruebas Nacionales de 30 puntos es evidente que ambas
convocatorias en el 2015 obtuvieron bajos promedios de puntaje, siendo esta situación aún
más notoria en la 2da convocatoria.
1.2. Porcentaje de respuestas correctas e incorrectas por dominios
Para una mejor comprensión de los resultados de las Pruebas Nacionales de Matemática para
Octavo Grado se analiza la estructura de la prueba. El contenido curricular se organiza en los
siguientes dominios: Numérico (número reales y operaciones), Algebraico (expresiones
algebraicas, ecuaciones e inecuaciones), Geométrico (geometría de coordenadas,
transformaciones geométricas y cuerpos geométricos), Métrico (perímetro, área y volumen) y el
de Estadística- probabilidad (tratamiento de la información
y cálculo de probabilidades
elementales).
La prueba nacional de matemática de octavo grado cuenta con 40 ítems en cada cuadernillo y
se utilizan dos cuadernillos distintos en cada convocatoria. La mayor cantidad de ítems
corresponde al dominio Números y operaciones con el 32% de la prueba total, como se puede
ver en la tabla siguiente.
4
Tabla No. 1.2
Composición de la prueba de Matemática y promedios de
porcentajes de respuestas correctas e incorrectas en ambas
convocatorias de las Pruebas Nacionales de Octavo Grado
del Nivel Básico
Ítems
%
en Prueba
%
RC
%
RI
1-Números y Operaciones
51
32.08
42.72
56.37
2-Algebra
32
20.13
39.30
59.84
3-Geometría
28
17.61
51.86
47.36
4-Mediciones
24
15.09
47.82
51.23
5-Estadística y Probabilidad
24
15.09
56.00
43.26
Total
159
100.00
Dominio
RC= respuestas correctas; RI= respuestas incorrectas
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Gráfico 1.1
Porcentajes de respuestas correctas e incorrectas, por
dominio en la Primera y Segunda Convocatoria de las
Pruebas Nacionales 2015 de Matemática, Octavo grado del
Nivel Básico
60.00
50.00
40.00
30.00
20.00
10.00
0.00
2.- Algebra
3.Geometría
4.Mediciones
%RC
1.- Números
y
Operaciones
42.72
39.30
51.86
47.82
5.Estadística y
Probabilidad
56.00
%RI
56.37
59.84
47.36
51.23
43.26
RC= respuestas correctas; RI= respuestas incorrectas
5
El resumen consolidado de ambas convocatorias muestra que el dominio que tuvo mayor
porciento de respuestas correctas fue Estadística y Probabilidad con 56% seguido por
Geometría con un 51.86%. Se evidencia además, que el mayor porciento de respuestas
incorrectas correspondió al dominio Algebraico con 59.84%, seguido por el de Números y
Operaciones con un 56.37% de respuestas incorrectas.
Los dominios Numérico, Algebraico y Métrico presentaron bajos resultados en relación a logros
de aprendizaje de los estudiantes, como se puede observar en el gráfico. Se observa que los
dominios de Geometría y de Estadística y Probabilidad alcanzaron mayores porcientos de
respuestas correctas que incorrectas.
Composición de la prueba de Matemática y porcentaje de respuestas
Tabla No. 1.3 correctas por dominios y por nivel de complejidad en ambas
convocatorias de Octavo Grado Nivel Básico 2015
Dominio
Cantidad de
ítems
/dominio
Proporción en
las pruebas (%)
Cantidad de ítems
según el nivel de
complejidad
Porcientos de
Respuestas Correctas
por nivel de
complejidad
1
2
3
1
2
3
1-Números y
Operaciones
51
32.08
12
26
13
50.64
40.61
39.62
2-Algebra
32
20.13
10
14
8
43.41
36.41
39.20
3-Geometría
28
17.61
19
8
1
55.77
46.04
24.11
4-Mediciones
24
15.09
2
17
5
47.41
53.88
27.39
5-Estadística y
Probabilidad
24
15.09
5
13
6
63.55
53.29
55.57
Total
159
100.00
48
78
33
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
De acuerdo con la Tabla No.1. 3, el mayor porciento de respuestas correctas se obtuvo en el
dominio de Estadística y Probabilidad en el nivel de complejidad 1 con 63.55%. Esto indica que
los estudiantes tienen mayor capacidad en comparar información a partir de una gráfica de
barras, en identificar la moda de un conjunto de datos, y en un gráfico de líneas en calcular la
probabilidad simple con la que se puede elegir un elemento a partir de un conjunto de datos.
El menor porciento de respuestas correctas se obtuvo en los dominios de Geometría y Métrica
en el nivel de complejidad 3 con 24.11% y 27.39% respectivamente. Este nivel de complejidad
en Geometría y Métrica implica aplicar principios y propiedades relacionadas con figuras y
cuerpos geométricos, comparar medidas de áreas y volúmenes de figuras, resolver problemas
en los que para su resolución se necesita inferir o calcular un dato a partir de una figura o un
gráfico, calcular áreas y volúmenes de figuras y/o cuerpos geométricos, manipular
correctamente la jerarquía de las operaciones aritméticas involucradas en los cálculos de áreas
y volúmenes.
6
También dada el área calcular el perímetro o un lado y dado el perímetro calcular el área, entre
otros.
En general, en varios dominios los porcentajes de respuestas correctas son más bajos en el
nivel 3 que implica resolver problemas y aplicar principios y por tanto una habilidad cognitiva
mayor.
1.3. Descripción de los ítems que resultaron fáciles y los que resultaron
difíciles en las Pruebas Nacionales de Matemática de Octavo Grado.
Dominio Numérico
Fáciles: Ubicar un número de una sola cifra decimal entre otros dos, de forma que queden
ordenados de mayor a menor. Identificar la mayor de un grupo de fracciones dadas.
Difíciles: Resolver un problema que involucre sustracción de fracciones. Calcular el valor
absoluto que contiene operaciones combinadas. Resolver un problema que involucre calcular
partes fraccionarias de un todo. Calcular el resultado que se obtiene al sumar números enteros
con signos diferentes. Obtener el resultado del valor absoluto de una fracción en donde el
numerador es una suma de enteros con signos diferentes
Dominio Algebraico
Fáciles: No se hallaron evidencias sobre ítems que resultaran fáciles en este dominio.
Difíciles: Calcular el valor numérico de una expresión algebraica de tres términos siendo los
valores de las variables números positivos y negativos. Resolver una ecuación de primer grado
con coeficientes de una sola cifra decimal.
Dominio Geométrico
Fáciles: Identificar la tesela usada para embaldosar un plano. Reconocer los elementos
geométricos del desarrollo de un cono y de un cilindro recto.
Difíciles: Rotar un segmento en el plano cartesiano. Calcular el área de un triángulo a partir de
un sistema de coordenadas cartesianas.
Dominio Métrico
Fáciles: Identificar dos figuras que tengan iguales áreas en una cuadrícula. Calcular el área de
una sola figura mostrada en una cuadrícula.
Difíciles: Calcular el área de un cuadrado a partir del perímetro. Dado el valor de un área
identificar el triángulo que la contenga. Calcular área lateral a partir del diámetro de la base y
de la altura de un cilindro. Calcular el área lateral de un cono recto.
7
Dominio de Estadística y Probabilidad
Fáciles: Analizar y comparar información a partir de una gráfica de barras. Identificar la moda
de un conjunto de datos. Calcular la probabilidad simple de elegir un elemento de un conjunto
dado. Identificar la moda en un gráfico de líneas.
Difíciles: Calcular la probabilidad de un evento con la condición “mayor o menor que” en una
serie ordenada de datos. Calcular la media aritmética de un conjunto de datos numéricos.
Calcular la probabilidad simple de un evento que involucra números racionales e irracionales.
1.4. Análisis de Algunos ítems de las Pruebas Nacionales
En el análisis pedagógico se presentan ítems que resultaron difíciles e ítems que resultaron
fáciles, en función de las categorías siguientes: información del ítem, dificultad, operación
cognitiva y contexto. Se agrega además una reflexión pedagógica con un enfoque didáctico–
metodológico. Para los ítems que resultaron difíciles se analizan los errores de los estudiantes
al elegir una opción que no es la correcta y para los que resultaron fáciles se analizan las
habilidades necesarias para elegir la opción correcta. En la sección siguiente se modelan con
ejemplos algunos casos.
1.4.1. Análisis pedagógico de los ítems que resultaron más fáciles
Ejemplo 1.
La cantidad de servicios de comida vendida por una cafetería durante una
semana se muestra en la gráfica. A partir de esta información selecciona la afirmación correcta.
A) El día de mayor venta fue el miércoles.
B) El martes la venta fue mayor que el sábado.
C) El viernes se vendió menos que el lunes.
D) El domingo la venta fue mayor que el jueves.
8
Información del ítem
Respuesta Correcta: D
Dominio: Estadística y probabilidad
Contenido: Lectura de datos suministrados en una gráfica de barras
Nivel Taxonómico o complejidad: 2
Dificultad: Este ítem resultó muy fácil, alcanzando 80.61 % de respuesta correcta.
Operación cognitiva: Este ítem demanda comparar los valores numéricos correspondientes a
las barras de la gráfica y establecer relaciones de mayor, menor o igual que, entre ellos.
Contexto: El contexto de este ítem es un gráfico mostrado en barras estadísticas que
favorecen la interpretación de la variable estudiada.
Reflexión Pedagógica: El contenido de este ítem posee información visual mostrada en una
gráfica de barras. A los estudiantes les resulta fácil interpretar las ventas de cada día de la
semana analizando las alturas de las barras. Es importante destacar que el contexto familiar
del ítem y la operación comparar valores explícitos contribuyeron al alto porcentaje de
estudiantes que lo contestó correctamente.
Ejemplo 2. ¿Cuál de las figuras sombreadas del dibujo tiene menor área?
A) P
B) Q
C) T
D) S
Información del ítem
Respuesta correcta: D
Dominio: Métrico
Contenido: Área de figuras en cuadrículas
Nivel taxonómico: 2
9
Dificultad: La gran mayoría de los estudiantes, alrededor de un 83.84% contestó
correctamente este ítem.
Operación cognitiva: Identificar la unidad de área en una cuadrícula y tomarla como unidad
de medida para calcular el área de figuras dadas.
Contexto: representación de figuras geométricas en una cuadrícula
Reflexión pedagógica: Resulta fácil Identificar la figura de menor área en una cuadrícula
debido a que el tamaño de la figura correspondiente a la opción correcta es obviamente la más
pequeña.
1.4.2. Análisis pedagógico de los ítems que resultaron más difíciles
Ejemplo 1. ¿Cuántos centímetros cuadrados de papel decorativo se necesitan para forrar un
gorro de cumpleaños como el que se muestra en la figura?
A) 314
SL=πrg
B) 392.5
C) 785
D) 847.8
Información del ítem
Respuesta correcta: C
Dominio: Métrico
Contenido: Área lateral de un cono
Nivel taxonómico: 2.
.
A
41.76
B
24.11
C
23.6
D
9.11
10
Dificultad: Este ítem fue contestado correctamente por el 23.6% de la población, lo que lo
hace un ítem difícil. Se observa que la mayoría eligió la opción A, que es el resultado de dividir
entre 3 el área lateral. Puede que lo confundan con el volumen del cono que va dividido entre 3.
Operación cognitiva: la demanda de este ítem consistía en aplicar la fórmula dada del área
lateral del cono y multiplicar números enteros y decimales.
Contexto: El enunciado del ítem se refiere a la actividad de construir un gorrito de cumpleaños.
Reflexión pedagógica: Se sugiere enfocar las actividades del proceso de enseñanza y
aprendizaje de este tema a situaciones de la vida que resulten familiares para el alumno.
4
Ejemplo 2. El perímetro de un triángulo es
2
longitud de un segundo lado es
A) 2
1
2
B) 3
7
12
C) 4
3
4
D) 1
1
6
3
1
1
4 cm, la longitud de uno de los lados es 3 cm y la
1
4 cm ¿Cuál es la longitud del tercer lado?
Información del ítem
Respuesta correcta: D
Dominio: Métrico
Contenido: Perímetro de figuras geométricas
Nivel taxonómico: 3
Dificultad: esté ítem fue contestado solo por un 17.96% de la población
Operación cognitiva: demanda encontrar el tercer lado de un triángulo conocidos 2 lados y el
perímetro así como también sumar y restar correctamente números fraccionarios
Contexto: se presenta un planteamiento de un problema que relaciona el dominio geométrico y
el métrico.
Reflexión pedagógica: la operación cognitiva de sumar y restar fracciones en el dominio
geométrico aumentaron la dificultad del ítem, por lo cual se deben desarrollar acciones que
privilegien la resolución de problemas en contextos diversos.
11
1.5. Contenidos de mayor dificultad de acuerdo a errores cometidos en
los ítems
A continuación se presentan algunos tipos de ítems en los que los estudiantes, mostraron
dificultades.
Según los análisis de las pruebas, los estudiantes de Octavo Grado muestran deficiencias en el
orden de las operaciones, en el manejo de los signos de números enteros, en el cálculo del
valor absoluto, en las operaciones con fracciones comunes y decimales, especialmente en la
potenciación y radicación.
El hecho de que no haya evidencia de ítems fáciles en el dominio algebraico, significa que los
ítems fueron de mediana o alta dificultad, mostrando los estudiantes bajo desempeño en este
dominio. Se debe reforzar el cálculo del valor numérico de una expresión algebraica, y la
resolución de ecuaciones e inecuaciones en una variable.
El siguiente ejemplo muestra los errores cometidos por los estudiantes en un ejercicio de valor
2
2
numérico; Si p= -4; q = 4, ¿cuál es el valor numérico de “  5 pq  3 p q  7 ”?
2
2
Evidentemente sustituyen las variables por los valores dados “  5(4)(4)  3(4) (4)  7 ”
pero se confunden con el orden de las operaciones y con los resultados de potencias que
2
2
tienen exponente par; por ejemplo, “  5(4)(4)  3(4) (4)  7 =20(16) + 3(-4)2(4) +7 = 320 +
3(-16) (4) +7= 320 – 52 +7= 275”, este proceso evidencia los errores con los signos.
En el dominio geométrico evidencian pocas habilidades en las transformaciones geométricas
por rotación, así como en el cálculo de áreas de figuras geométricas en cuadrículas. En este
aspecto se resalta la importancia de las conexiones existentes entre el dominio Geométrico y el
Métrico.
El siguiente ejemplo muestra los errores cometidos por los estudiantes en un ítem de rotación;
¿Cuál segmento corresponde a una rotación de 360° del segmento RS respecto al origen? La
respuesta correcta sería RS pero la mayoría eligió R3S3
12
En el dominio Métrico muestran pocas habilidades en el cálculo de áreas y volúmenes de
cuerpos geométricos. También los estudiantes presentaron dificultades en el cálculo y
comparación de áreas y perímetros de regiones cuadradas, por ejemplo al calcular las áreas
de 2 cuadrados como los mostrados en la figura
Asumen que si el lado de uno es el doble del lado del otro entonces se da la misma razón
entre las áreas, es decir que para determinar cuántas veces es más grande el área del
cuadrado grande que el área del menor dividen las longitudes de los lados, de los 2
2L
2
cuadrados ( L
) asumiendo que el área del mayor cuadrado es 2 veces el área del
menor, cuando en realidad el área del mayor es 4 veces el área del menor.
Se evidencian dificultades para calcular una probabilidad simple en un espacio muestral
dado, especialmente cuando la estimación de probabilidad del evento incluye la condición
de que el evento favorable sea mayor, igual o menor que un valor dado. También se
evidencian dificultades para estimar la probabilidad de un evento cuando el espacio muestral
se presenta como una lista de números racionales e irracionales. Muestran poca habilidad en
el cálculo de medidas de tendencia central, confundiendo habitualmente la media aritmética
con la mediana.
En conclusión, los dominios con más debilidades fueron el Algebraico, Numérico y Métrico
cuyos porcientos de respuestas correctas no alcanzaron el 50%.
En los niveles de complejidad cabe destacar que los más bajos fueron el nivel 3 de los
dominios Geométrico y Métrico, por tanto los estudiantes tuvieron pocas habilidades de
resolución de problemas usando la geometría y la métrica.
También mostraron debilidades en el nivel 2 de Álgebra, o sea, resolviendo ejercicios que
involucran uno o dos procesos. Entre los contenidos que los estudiantes contestaron menos
están las ecuaciones e inecuaciones, expresiones algebraicas y números y operaciones.
Una meta realista para este grado sería mejorar los aprendizajes en los dominios Numérico,
Algebraico y Métrico y en la resolución de problemas para mover a los estudiantes a niveles de
complejidad superiores.
13
II. Tercer Ciclo de Adultos
2.1. Puntaje Promedio en Las Pruebas Nacionales de Matemática 2015
A continuación se presentan los puntajes promedios obtenidos en las pruebas nacionales de
matemática del 3er ciclo de adultos en la primera y segunda convocatoria.
Promedio de puntajes y total de estudiantes examinados por
Tabla No. 2.1. convocatoria en las Pruebas Nacionales de Matemática 2015, en el
Tercer Ciclo de Adultos del Nivel Básico.
Tercer Ciclo de Adultos
Convocatorias
Promedio de puntajes
Total de examinados
Primera
15.11
29,376
Segunda
14.44
4,652
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Como se observa en la tabla el puntaje promedio obtenido en la primera convocatoria es
superior al obtenido en la segunda pero en ambos casos es bajo, con respecto a la escala
establecida (30 puntos).
2.2. Porcentajes de respuestas correctas e incorrectas por dominios
La prueba nacional de matemática de adultos cuenta con 40 ítems en cada cuadernillo y se
utilizan dos cuadernillos distintos en cada convocatoria. La mayor cantidad de ítems
corresponde al dominio Números y operaciones con el 32.5% de la prueba total, como se
puede ver en la tabla siguiente.
14
Composición de la prueba de matemática y porcentajes de
respuestas correctas e incorrectas en ambas convocatorias de las
Tabla No. 2.2
Pruebas Nacionales 2015 en el Tercer Ciclo de Adultos del Nivel
Básico
Dominio
Ítems
% en Prueba
%RC
%RI
Números y Operaciones
52
32.50
45.53
52.28
Geometría
44
27.50
44.25
53.44
Mediciones
32
20.00
38.84
58.83
Estadística y Probabilidad
32
20.00
59.68
38.34
Total
160
100.00
RC= respuestas correctas; RI= respuestas incorrectas
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Porcentajes de respuestas correctas e incorrectas por
cada dominio en la Primera y Segunda Convocatoria de
Gráfico 2.1
las Pruebas Nacionales 2015 de Matemática, Tercer ciclo
de Adultos del Nivel Básico
60.00
Título del eje
50.00
40.00
30.00
20.00
10.00
0.00
2.- Geometría
3.- Mediciones
%RC
1.- Números y
Operaciones
45.53
44.25
38.84
4.- Estadística
y Probabilidad
59.68
%RI
52.28
53.44
58.83
38.34
Fuente: Datos de la tabla 5. RC= respuestas correctas; RI= respuestas incorrectas.
15
Según se muestra en el resumen consolidado, el dominio que obtuvo el mayor porcentaje de
respuestas correctas en ambas convocatorias fue Estadística y Probabilidad con un 59.68%,
seguido de números y operaciones con 45.53% de respuestas correctas. El mayor porcentaje
de respuestas incorrectas lo obtuvo mediciones con un 58.83% seguido por Geometría con un
52.28% de respuestas incorrectas. En general, los porcentajes de respuestas incorrectas son
más altos que los porcentajes de respuestas correctas en todos los dominios, excepto en el
dominio de Estadística y Probabilidad.
Tabla No. 2.3
Dominios
Composición de la prueba de matemática y porcentaje de
respuestas correctas por dominios y nivel de complejidad en
ambas convocatorias, Tercer Ciclo de Adultos del Nivel Básico
2015
Cantidad
de
ítems
/dominio
Proporción
en
la prueba
(%)
Cantidad de
ítems
según el nivel
de
complejidad
Porcentajes
Respuestas
Correctas por nivel
de complejidad
1
2
3
1
2
3
1-Números y
Operaciones
52
32.50
17
23
12
45.02
44.57
48.08
2-Geometría
44
27.50
27
11
6
49.61
41.48
25.19
3-Mediciones
32
20.00
4
11
17
49.20
40.83
35.12
4-Estadística y
Probabilidad
32
20.00
11
15
6
67.38
58.28
49.07
Total
160
100.00
59
60
41
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
De acuerdo con la tabla No. 2.3, los mayores porcientos de respuestas correctas se lograron
en el dominio de Estadística y Probabilidad en el nivel de complejidad 1 con 67.38%. Esto
significa que los estudiantes reconocen conceptos estadísticos fundamentales, identifican datos
estadísticos explícitos en tablas y gráficas y reconocen los diferentes tipos de gráficas
estadísticas.
El menor porciento de respuestas correctas se obtuvo en el dominio de Geometría en el nivel
de complejidad 3 con 25.19%. Esto muestra que los estudiantes tuvieron pobre desempeño en
la resolución de problemas geométricos, y en las conexiones de la geometría con la realidad y
otras áreas del conocimiento, establecer relaciones e inferencias en contextos geométricos
diversos.
16
2.3. Descripción de los ítems que resultaron fáciles y los que resultaron
difíciles en las Pruebas de Matemática en Tercer Ciclo de Adultos.
Dominio Numérico
Fáciles: Calcular la mitad del precio de un producto dado su precio total.
Difíciles: Calcular la altura de un triángulo isósceles conocidos la base y uno de los lados
iguales.
Calcular distancias con números de una cifra decimal.
Calcular potencias que combinan exponentes positivos y negativos.
Efectuar operaciones combinadas con números enteros.
Comparar expresiones con valor absoluto.
De un gráfico dividido en porciones iguales identificar la fracción que representa una parte que
se ha sombreado y expresarla en decimal.
De un grupo de decimales identificar cual es periódico puro.
Dominio Geométrico
Fáciles: No se encontró evidencia de ítems “fáciles” en este dominio.
Difíciles: Identificar ángulos opuestos por el vértice en dos rectas paralelas cortadas por una
secante.
Calcular a qué distancia se encuentra el pie de una escalera recostada de una pared. Identificar
un conjunto de puntos ubicados sobre una misma recta en el plano cartesiano.
Dominio Métrico
Fáciles: No se encontró evidencia de ítems “fáciles” en este dominio.
Difíciles: Calcular el volumen de un cono conocido su radio y su altura.
Comparar los volúmenes de dos recipientes en forma cilíndrica, conocidos el radio y la altura
de cada uno.
Dominio Estadística y Probabilidad
Fáciles: Analizar y comparar información a partir de un gráfico de barras.
Difíciles: No se encontró evidencia de ítems “difíciles” en este dominio.
17
2.4. Análisis de los ítems que resultaron más fáciles y más difíciles
Se presenta un análisis pedagógico de algunos de los ítems que resultaron fáciles y difíciles
en función de los errores cometidos por los estudiantes, fundamentado en las categorías:
información del ítem, dificultad, operación cognitiva y contexto. Además se agrega una reflexión
pedagógica con algunas recomendaciones didáctico-metodológicas y se modelan algunos
ejemplos.
2.4.1. Análisis pedagógico de los ítems que resultaron más fáciles
Ejemplo 1: ¿En qué año los ingresos fiscales fueron mayores según muestra el siguiente
gráfico?
A) 2000
B) 2004
C) 2005
D) 2006
Información del ítem
Respuesta correcta: B
Dominio: Estadística y probabilidad
Contenido: Gráfico de columnas
Nivel taxonómico: 1
Dificultad: Este ítem fue contestado por el 74.39 % de los estudiantes, es un ítem fácil.
Operación cognitiva: Leer datos a partir de una gráfica de barras e identificar la columna de
mayor frecuencia.
Contexto: Contexto visual presentado en un gráfico de barras
Reflexión pedagógica: Este tipo de gráfica es común en los medios de comunicación impresa
y televisada por lo que resulta familiar para el alumno. La palabra “ingresos mayores” agrega
facilidad ya que se puede asociar con la columna más alta. En general los estudiantes
mostraron un dominio aceptable de lo que se preguntó sobre estadística.
18
Ejemplo 2: Un producto se vende a $80 la libra. Si José compra un cuarto de libra, ¿Cuántos
pesos debe pagar?
A) $20
B) $40
C) $60
D) $80
Información del ítem
Respuesta correcta: A
Dominio: Numérico
Contenido: División de números enteros o multiplicación de un entero por una fracción.
Nivel taxonómico: 3
Grado de dificultad: El 77.65% de los estudiantes contestó correctamente este tipo de ítem.
Operación cognitiva: El procedimiento es multiplicar 80 por ¼ o dividir 80 entre 4.
Contexto: Una situación polémica de la vida cotidiana de los estudiantes.
Reflexión pedagógica: Este ítem resultó fácil para la mayoría de los estudiantes porque se
enmarca en situaciones del diario vivir, como la compra pesada o medida de un producto.
2.4.2. Análisis pedagógico de los ítems que resultaron más difíciles.
Ejemplo 1: Una escalera se recuesta en una pared como se muestra en el gráfico. ¿A qué
distancia de la pared está la base de la escalera?
A) 16 pies
B) 6 pies
C) 8 pies
D) 4 pies
19
Información del ítem
Respuesta correcta: C
Dominio: Geométrico
Contenido: Teoremas de Pitágoras
Nivel taxonómico: 3
.
A
26.71
B
23.38
C
20.18
D
27.78
Dificultad: Este ítem fue contestado por el 20.18% de los estudiantes, lo que lo hace un ítem
difícil. Para calcular el cateto que representa la distancia, el estudiante tiene que aplicar el
teorema de Pitágoras, dada la hipotenusa y un cateto. En general todas las opciones presentan
un porciento similar, lo que indica que hay poco dominio del tema. La opción D que es la más
contestada y evidencia que los estudiantes están restando el cateto dado a la hipotenusa. Los
que eligen la opción A están sumando la hipotenusa y el cateto dado y, los que eligen la opción
B asumen que los dos catetos tienen la misma medida.
Operación cognitiva: Identificar el triángulo como rectángulo e inferir que hay que aplicar el
teorema de Pitágoras.
Contexto: Una escalera recostada de una pared es una situación conocida para la mayoría de
los alumnos y es usada en los textos escolares.
Reflexión pedagógica: Se justifica la dificultad del ítem porque es un problema que no
menciona directamente el teorema de Pitágoras, ni presenta el gráfico, sino que el estudiante
debe inferir su uso para obtener la respuesta correcta. El hecho de que directamente sumen o
resten los lados del triángulo sin aplicar el teorema de Pitágoras indica muy poco dominio del
tema. Por tanto se recomienda presentar problemas de este tipo en las actividades de
enseñanza aprendizaje, que no incluyan el gráfico y que el estudiante tenga que hacerlo para
visualizar mejor la situación. Por otro lado, se sugiere dedicar más tiempo a la resolución de
problemas usando el teorema de Pitágoras.
Ejemplo
2: ¿Cuál
centímetros de altura?
A) 150.72 cm3
es el volumen de un cono que mide 8 centímetros de radio y
12
Sugerencia
B) 2,411.52 cm3
C) 803 .84 cm3
D) 301.44 cm3
20
Información del ítem
Respuesta correcta: C
Dominio: Geometría
Contenido: Volumen de cuerpos geométricos.
Nivel taxonómico: 2
.
A
40.96
B
26.08
C
19.94
D
10.34
Grado de dificultad: El 19.94% de los estudiantes contestó correctamente este tipo de ítem,
por lo que es un ítem difícil. Su dificultad está relacionada con la combinación de operaciones
que involucra en el proceso de resolución: potenciación, producto y división. Además el ítem no
presenta figura lo que también puede influir en su complejidad. Más del 40% de los estudiantes
elige la opción A, que es el resultado de tomar para el radio la mitad del valor dado y no
elevarlo al cuadrado. Aproximadamente el 26% elige la opción B porque el producto no lo
están dividiendo entre 3.
Contenido del ítem: Volumen de un cono.
Operación cognitiva: para contestar correctamente este ítem el estudiante primero tiene que
sustituir los datos del enunciado en la fórmula dada, luego desarrollar las operaciones de
potencia, producto y división de números.
Reflexión pedagógica: Aunque este ítem envuelve combinación de las operaciones
aritméticas de potencia, producto y división, se esperaba que resultara más fácil debido a que
la fórmula estaba dada, que es el punto de partida. Al dar la fórmula el ítem se convierte en un
valor numérico de una expresión algebraica; pero la dificultad muchas veces se refleja por el
dominio en las operaciones involucradas. Se recomienda enfatizar la resolución de problemas
reales que involucren cuerpos geométricos con y sin dibujo para desarrollar la habilidad de
modelar gráficamente los problemas.
21
2.5. Contenidos de mayor dificultad de acuerdo a errores cometidos en
los ítems
Los estudiantes muestran poco dominio en conocimientos, habilidades y destrezas en los
siguientes contenidos:
Identificación de números racionales e irracionales en su forma decimal, tampoco discriminan
correctamente entre decimales periódicos y no periódicos.
En la resolución de problemas que involucran división de dos enteros para tomar como
respuesta el residuo, toman el resultado como si fuera el residuo, se recomienda hacer énfasis
en los elementos de la división.
Al sumar números con una cifra decimal, colocan el punto decimal de forma incorrecta como se
ilustra a continuación 0.6  0.5  0.11 , cuando lo correcto es que como cada sumando tiene
una cifra decimal el resultado también tendrá una cifra decimal, así: 0.6  0.5  1.1 .
Cuando se le pide calcular un producto de potencias con exponentes positivos y negativos,
desarrollan el producto como una suma buscando MCM; o sea al resolver las operaciones
en un ítem como este
3
1
1
3 9  5
escriben
1 1
3 *
9 5 y luego
obtienen como resultado
14
1 1
*
45 sumando 9 5 en vez de multiplicarlo, que es lo correcto.
Al resolver una división de un número negativo y uno positivo el cociente lo toman como
positivo. Al calcular la distancia entre dos puntos en una recta numérica dada una escala de un
½, suman las partes correctamente pero le agregan al resultado la escala dada como si fuera
una unidad de medida.
En Geometría también se detectaron algunas debilidades de las que se pueden citar las
siguientes: al calcular la altura de un triángulo isósceles conocido la base y uno de los lados
iguales, le resulta difícil aplicar el teorema de Pitágoras para calcular la altura, al no dividir la
base entre 2. Al pedirle elegir los puntos que están en una recta vertical eligen los que están en
una recta oblicua. Al calcular la longitud de un cateto en un triángulo rectángulo restan
directamente a la hipotenusa la longitud del cateto dado, por ejemplo si la hipotenusa mide 9cm
y un cateto mide 5cm obtienen como medida para el otro 9cm-5cm=4cm. También Confunden
ángulos opuestos por el vértice con los alternos internos. En Métrica las mayores deficiencias
detectadas se relacionan con el cálculo de volúmenes y áreas. Por ejemplo al calcular el
volumen de un prisma rectangular multiplican solamente dos lados. Al calcular el área lateral de
un cilindro con la fórmula A= 2πrh, usan la mitad del radio, cuando deben tomarlo entero. Al
calcular el volumen de un cono dado la fórmula no elevan el radio al cuadrado y en lugar de
dividir entre tres dividen entre dos. En general, las mayores dificultades están en Mediciones,
Geometría y Números. Los estudiantes tuvieron dificultades en el trabajo con ángulos
especiales, medidas de ángulos, cálculo de perímetros, áreas y volúmenes. Con relación a los
niveles de complejidad mostraron dificultades en el nivel 3, o sea, resolviendo problemas
aplicando Geometría y Métrica. Además, los estudiantes mostraron poco dominio de las
operaciones con los números racionales así como en la Geometría de coordenadas y el
teorema de Pitágoras.
22
III. Nivel Medio Modalidad General
3.1. Puntaje Promedio en Pruebas Nacionales de Matemáticas 2015
A continuación se presentan los puntajes promedios obtenidos en las pruebas nacionales de
matemática en el nivel medio modalidad general en la primera y segunda convocatoria.
Tabla No. 3.1
Promedio de puntaje y total de estudiantes examinados en la
Prueba Nacional de Matemática 2015, por Convocatoria en el
Nivel Medio Modalidad General
Nivel Medio Modalidad General
Convocatorias
Puntaje promedio
Primera
16.82
Segunda
15.81
Total de examinados
108,725
51,426
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad.
Como se observa en la tabla No. 3.1 el puntaje promedio obtenido en la primera convocatoria
fue de 16.82 y en la segunda fue 15.81. Puede notarse que el puntaje promedio en la primera
convocatoria fue ligeramente superior al obtenido en la segunda y si se visualiza con la escala
de 0-30 puntos en ambos casos es bajo.
3.2. Porcentajes de respuestas correctas e incorrectas por dominios
La prueba nacional de matemática de Media modalidad general cuenta con 50 ítems en cada
cuadernillo y se utilizan dos cuadernillos distintos en cada convocatoria. La mayor cantidad de
ítems corresponde al dominio de Algebra con el 36% de la prueba total, como se puede ver en
la tabla siguiente.
23
Composición de la prueba de Matemática y promedios de
porcentajes de respuestas correctas e incorrectas en ambas
convocatorias de las Pruebas Nacionales 2015 en el Nivel Medio
Modalidad General
Tabla No. 3.2.
Dominio
Ítems
% en Prueba
%RC
%RI
1-Lógica y Conjunto
24
12.06
46.10
53.33
2-Algebra
71
35.68
43.31
55.94
3-Geometría
36
18.09
42.53
56.82
4-Trigonometría
24
12.06
38.20
60.83
5.- Estadística y Probabilidad
28
14.07
48.56
50.81
6.- Cálculo
16
8.04
36.81
62.24
Total
199
100.00
RC= respuestas correctas; RI= respuestas incorrectas
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad
Gráfico 3.1
Porcentajes de respuestas correctas e incorrectas por cada uno de
los dominios en la Primera y Segunda Convocatoria de las Pruebas
Nacionales 2015 de Matemática, Nivel Medio, Modalidad General
60.00
50.00
40.00
30.00
20.00
10.00
0.00
1.- Lógica y
Conjunto
2.- Algebra
3.Geometría
4.Trigonomet
ría
6.- Cálculo
38.20
5.Estadística
y
Probabilida
d
48.56
%RC
46.10
43.31
42.53
%RI
53.33
55.94
56.82
60.83
50.81
62.24
36.81
RC= respuestas correctas; RI= respuestas incorrectas
24
Según muestra la tabla No.3.2 y su gráfica, el dominio que tuvo el mayor porcentaje de
respuestas correctas fue el de Estadística, Probabilidad y Análisis Combinatorio, con 48.56%
seguido por el de Lógica y Conjuntos con un 46.10%; el dominio que tuvo mayor porcentaje de
respuestas incorrectas fue Cálculo con 62.24% seguido por el Trigonométrico con 60.83%. En
general todos los dominios tuvieron más respuestas incorrectas que correctas en las dos
convocatorias y cabe resaltar que los porcentajes de respuestas correctas estuvieron por
debajo del 50% en todos los dominios.
Composición de la prueba de matemática y porcientos de respuestas
Tabla No. 3.3 correctas por dominios y nivel de complejidad en ambas convocatorias
2015, Nivel Medio Modalidad General.
Cantidad
de
ítems
/dominio
Proporción
en
la prueba
(%)
1-Lógica y Conjunto
24
2-Algebra
Dominios
Cantidad de
ítems
según el nivel
de complejidad
Porciento de
Respuestas Correctas
Por nivel de
complejidad
1
2
3
1
2
3
12.06
13
8
3
43.46
53.08
38.93
71
35.68
21
35
15
52.79
32.52
55.20
3-Geometría
36
18.09
17
12
7
42.86
43.41
40.23
4-Trigonometría
24
12.06
5
10
9
40.14
39.64
35.53
5-Estadística y Probabilidad
28
14.07
13
10
5
57.23
41.60
39.93
6-Cálculo
16
8.04
7
4
5
34.71
31.56
43.94
Total
199
100.00
76
79
44
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad.
La tabla No. 3.3 muestra la distribución de ítems evaluados en las pruebas por niveles de
complejidad según el dominio, así como también el porciento de respuestas correctas en cada
nivel.
En el nivel de complejidad 1, el dominio que tiene mayor porciento de respuestas correctas es
el de Estadística y Probabilidad con un 57.23%, o sea, que más del 50% de los estudiantes
pudieron identificar correctamente conceptos y datos sobre Estadística. Los estudiantes
mostraron ser capaces de: definir conceptos estadísticos y de probabilidad e identificar datos,
expresiones y notación estadística.
En el nivel de complejidad 2 el dominio de mayor porciento de respuestas correctas fue el de
Lógica y Conjuntos con un 53.08%. Esto deja claro que más de la mitad de los estudiantes
contestaron correctamente los ítems sobre hacer inferencias lógicas simples, identificar tipos de
razonamiento lógicos, establecer la veracidad o falsedad de una proposición lógica, establecer
relaciones entre los elementos de dos o más conjuntos, operar con conjuntos, entre otros.
En el nivel de complejidad 3 el dominio de mayor porciento de respuestas correctas es el de
Álgebra con un 55.20%. Los estudiantes fueron capaces de resolver ejercicios algebraicos que
involucran más de dos procesos algebraicos, de resolver problemas usando esquemas, tablas,
gráficas y establecer conexiones en áreas diferentes.
25
3.3. Descripción de los ítems que resultaron fáciles y los que resultaron
difíciles en las Pruebas Nacionales de Matemática del Nivel Medio
Modalidad General.
Dominio Lógico Conjuntista
Fáciles: No se encontró evidencia de ítems fáciles en este dominio.
Difíciles: Identificar la ley de silogismo entre varias expresiones en forma argumental.
Encontrar el conjunto potencia de un conjunto.
Dominio Algebraico
Fáciles: Dado un punto en el plano gaussiano, identificar el número complejo que le
corresponde y dado el complejo identificar el punto del plano que le corresponde.
Traducir una expresión matemática al lenguaje cotidiano que involucra un producto y una
suma. Traducir un problema a un sistema de ecuaciones simultáneas con dos variables y
resolverlo. Identificar el término que sigue en una secuencia de números para que sea una
progresión aritmética.
Difíciles: Identificar el proceso correcto de simplificar una fracción que demanda dos casos de
factorización: diferencia de cuadrados y factor común monomio.
Resolver un problema que demanda la traducción de un enunciado en una ecuación cuadrática
y luego resolverla. Hallar las soluciones de una ecuación cuadrática completa dada en la forma
ax 2  bx  c y en la forma ax2  c  0 . Encontrar los valores de a y b desconocidos en dos
números complejos en forma binómica, para establecer la igualdad. Dados el primer término y
la diferencia común escribir los “n” primeros términos de una progresión aritmética. Determinar
la ecuación de la recta dada la pendiente y un punto que pertenece a la recta. Encontrar la
solución de una inecuación graficada en el plano cartesiano. Encontrar el valor mínimo que
toma una variable en una desigualdad que contiene el signo de desigualdad x≥4. Identificar la
expresión algebraica que corresponde a un enunciado dado. Dado un gráfico cartesiano donde
se representa el conjunto solución de una relación, identificar el dominio y el codominio de la
relación.
26
Dominio Geométrico
Fáciles: Identificar el centro de rotación de una figura geométrica.
Difíciles: Convertir a grados sexagesimales la medida de un ángulo expresado en una
fracción de radianes. Calcular la ecuación general de la circunferencia a partir de las
coordenadas del centro y del radio. Dado un triángulo en el plano cartesiano calcular las
coordenadas del triángulo simétrico respecto a un eje coordenado. Resolver un problema que
demanda establecer la igualdad entre los volúmenes de dos cilindros para determinar la altura
de uno de ellos. Identificar la bisectriz de un ángulo de un triángulo.
Dominio Trigonométrico
Fáciles: Dada la razón trigonométrica de un ángulo, identificar el triángulo que la define.
Difíciles: Usar la función apropiada para calcular la altura de un triángulo rectángulo conocidos
un ángulo y un lado. Calcular el valor numérico de una expresión trigonométrica que involucra
funciones de los ángulos de 30°, 60° y 90°. Convertir la medida de un ángulo expresado en
radianes a grados sexagesimales. Verificar si una igualdad entre expresiones trigonométricas
es una identidad. Utilizar una función trigonométrica para encontrar valores desconocidos en un
triángulo rectángulo.
Dominio Estadístico-Probabilístico
Fáciles: Resolver un problema de probabilidad simple dados dos eventos complementarios en
un espacio muestral. Identificar la categoría con menor frecuencia en un gráfico de líneas.
Difíciles: Dado el total de objetos y una cantidad defectuosa de esos objetos calcular la
probabilidad de sacar un objeto defectuoso. Determinar el número de combinaciones que se
pueden formar con un conjunto de (n) números dado, tomando “r” en cada arreglo. Tomar
decisiones al comparar las variaciones de una función donde la variable toma valores
distintos. De un gráfico circular elegir la variable que cumpla con determinadas condiciones.
Dominio del Cálculo
Fáciles: No se encontró evidencia de ítems fáciles en este dominio.
Difíciles: Calcular la segunda derivada de una función cuya expresión es un monomio y
demanda aplicar la regla de la potencia. Hallar el límite de una función racional donde se
presenta una indeterminación del tipo 0/0.
27
3.4. Análisis de los ítems que resultaron más fáciles y más difíciles
Se presenta un análisis pedagógico de algunos de los ítems que resultaron fáciles y difíciles
en función de los errores que cometen los estudiantes, fundamentado en las siguientes
categorías: información del ítem, dificultad, operación cognitiva y contexto. Además se agrega
una reflexión de carácter didáctico-metodológica y se modelan algunos ejemplos.
3.4.1 Análisis pedagógico de los ítems que resultaron más fáciles
Ejemplo 1. En un curso de 42 estudiantes hay 28 que hacen deportes. Si se elige un
estudiante al azar para que los represente en una reunión, se puede concluir que hay
A) más probabilidad de que haga un deporte.
B) más probabilidad que no haga deporte.
C) igual probabilidad que haga o no haga deporte.
D) el doble de probabilidad que haga deporte.
Información del ítem
Respuesta correcta: A
Dominio: Estadístico y probabilístico
Contenido: Probabilidad simple
Nivel taxonómico: 2
Dificultad del ítem: Este ítem es fácil porque fue contestado por el 82% de los estudiantes.
Operación cognitiva: primero para encontrar los que no hacen deportes el estudiante tiene
que restarle al total los que hacen deportes, luego calcular la probabilidad de cada grupo y
compararlas.
Contexto: la información se relaciona con el contexto escolar.
Contenido: Probabilidad simple, cuyo método más conocido es la regla de Laplace. Con esta
regla el estudiante expresa las probabilidades como fracciones y simplifica dichas fracciones.
Reflexión pedagógica: La facilidad del ítem puede estar justificada por el contexto y el
contenido. El contexto alude a una situación familiar del alumno, y el contenido implica expresar
números en fracciones al aplicar la regla de Laplace.
28
Ejemplo 2- ¿Con cuál de los triángulos se puede definir la razón sen A=1/4?
A) 1
B) 2
C) 3
D) 4
Información del ítem
Respuesta correcta: A
Dominio: Trigonométrico
Contenido: Razones trigonométricas en el triángulo rectángulo
Nivel taxonómico: 1
Dificultad del ítem: El ítem resultó fácil porque el 80% de los estudiantes lo contestó
correctamente.
Contenido del ítem: el contenido está relacionado con la definición de la razón trigonométrica
Seno, para un ángulo agudo de un triángulo rectángulo. Esto incide en la facilidad del ítem ya
que implica una definición.
Operación cognitiva: Para contestar correctamente este ítem es necesario que el estudiante
evoque la definición de la razón trigonométrica Seno de un ángulo agudo en el triángulo
rectángulo, para luego identificar de entre los triángulos dados en cuál se cumple que dicha
razón para el ángulo A sea ¼. Las operaciones mentales de recordar e identificar son
operaciones cognitivas simples.
Contexto: El ejercicio se presenta en un contexto trigonométrico.
Reflexión pedagógica: el contexto del ítem aparece tal cual se presenta en la mayoría de los
textos escolares actuales, además implica identificar una figura, lo que pudiera contribuir a que
la mayoría de los estudiantes lo contestara correctamente.
29
3.4.2 Análisis pedagógico de los ítems que resultaron más difíciles
25  m 2
2
Ejemplo 1. Se le pidió a cuatro estudiantes que simplificaran la expresión 5m  m , ¿cuál de
ellos lo hizo correctamente?
Información del ítem
Respuesta correcta: D
Dominio: Algebraico
Contenido: Simplificación de expresiones algebraicas
Nivel taxonómico: 3
.
A
23.52
B
31.18
C
29.33
D
15.37
30
Dificultad del ítem: Este ítem fue contestado correctamente por el 15.37% de los estudiantes,
por lo que es un ítem difícil. La opción A fue elegida por el 23.52% de los estudiantes,
demostrando que tienen problemas con la simplificación y poco dominio de la propiedad
distributiva para la división entre monomios. La opción B fue elegida por el 31.18% porque
cancelaron (5  m ) del numerador con (5  m) del deno min ador como si fueran iguales.
La opción C fue elegida por un 29.33% de los alumnos mostrando aplicación inapropiada de la
propiedad distributiva, y además se refleja que algunos estudiantes trabajan en álgebra como si
fuera en aritmética tomando siempre el resultado como un número.
2
Operación cognitiva: Para contestar correctamente el ítem el estudiante necesita aplicar dos
casos de factorización: una diferencia de cuadrados en el numerador y factor común en el
denominador y luego simplificar factores iguales del numerador y denominador, para obtener
como respuesta una expresión algebraica. Los casos de factorizaciones involucradas son
procesos algebraicos que incluyen definiciones y operaciones complejas, pero se evidencia que
la mayoría están factorizando y simplificando incorrectamente cuando se presenta el ejercicio
en un contexto puramente algebraico.
Reflexión pedagógica: Es importante que desde la docencia en el aula se incluyan ejercicios
que combinen casos de factorización algebraica y además demanden simplificar. Por otro lado
se recomienda a los docentes hacer énfasis en que cuando se trabaja con Álgebra, el resultado
puede ser tanto un número como una expresión. Las respuestas incorrectas de los estudiantes
muestran que tienen dificultades para factorizar una expresión usando la diferencia de
cuadrados y por factor común monomio, además de simplificar una expresión racional que
tiene un factor repetido en el numerador y denominador.
Ejemplo 2. ¿Cuál es la ecuación de la circunferencia cuyo centro está en el punto
(5, 2 ) y su radio mide 3 cm ?
A)
x 2  y 2  20  0
B)
x 2  y 2  10 x  4 y  20  0
C)
x 2  y 2  10 x  4 y  12  0
D)
x 2  y 2  10 x  4 y  29  0
31
Información del ítem
A
B
C
D
13.22
23.33
35.36
26.97
Respuesta correcta: B
Dominio: Algebraico
Contenido: Ecuación de la circunferencia
Nivel taxonómico: 3
.
A
13.22
B
23.33
C
35.36
D
26.97
Dificultad del ítem: el 23.33% de los estudiantes eligió la opción B que es la correcta, por lo
que este ítem resultó difícil. Estos estudiantes escribieron la ecuación en forma ordinaria y
desarrollaron correctamente los cuadrados y simplificaron para obtener la ecuación general de
la circunferencia. El 35.36% eligió la opción C, y esta opción se obtiene cuando asumen
incorrectamente que (-2)2 =-4 y al operar los términos independientes obtienen 12. La opción D
fue elegida por el 26.97%, omitieron restar el cuadrado del radio.
Operación cognitiva: Para contestar correctamente el ítem el estudiante tenía que conocer la
( x  h) 2  ( y  k ) 2  r 2
ecuación de la circunferencia en la forma
, luego sustituir los valores
del centro por h y k y el radio r por 3. Una vez conseguida la ecuación ordinaria tienen que
transformarla a la forma general. La complejidad del ítem viene dada porque combina varias
operaciones como sustituir, desarrollar el cuadrado de una suma y/o diferencia de dos
cantidades, ordenar y simplificar.
Reflexión pedagógica: Se recomienda practicar con los estudiantes la ecuación de la
circunferencia en sus diferentes formas: ordinaria, canónica y general, y convertir de una forma
a la otra.
32
3.5. Contenidos de mayor dificultad de acuerdo a errores cometidos en
los ítems
En este apartado se identifican algunos errores que cometieron la mayoría de los estudiantes
en algunos ítems.
Al identificar la ley de silogismo o transitividad entre condicionales eligen la expresión
( p  q)  (q  r )  ( p  r ) como correcta mostrando que pocos dominan este concepto, en
este caso la segunda conjunción de izquierda a derecha debe sustituirse por la flechita de la
condicional. Al calcular el conjunto potencia de un conjunto dado omiten el conjunto vacío y el
mismo conjunto.
En Álgebra los mayores fallos estuvieron en identificar las raíces de una ecuación cuadrática.
Además, al identificar el proceso correcto de resolver una ecuación simple de primer grado de
la forma 2x=5+3x, escriben como correcto 2x+3x=5. Este error se puede tratar siempre que se
resuelva la ecuación aplicando las propiedades de la igualdad, en vez de “pasar términos de un
lado a otro cambiando el signo”, truco que se ha inventado para acortar el proceso de
resolución. Dada una función graficada en el plano, identifican el dominio de la función como si
fueran pares ordenados en el plano, y no como valores del eje x. Al identificar el conjunto de
parejas ordenadas que corresponde a la solución de una función exponencial eligen los pares
que tienen su abscisa y ordenada negativa, esto indica poco dominio del concepto de función
5m
m , dan como respuesta 5,
exponencial. Cuando simplifican una expresión del tipo
5
1
aplicando incorrectamente la propiedad cancelativa; lo correcto es que expresen así m
. Al
expresar en forma algebraica “la unidad más ocho veces un número” obtienen 9, porque lo
suman haciendo una interpretación como 1+8=9; en lugar de plantear x+8x.
En Geometría confunden la bisectriz de un triángulo con mediana y bisectriz. Al buscar
el simétrico respecto al eje y de un punto le cambian el signo a la ordenada cuando lo
correcto es cambiar el signo a la abscisa x.
En Trigonometría al identificar el triángulo que define la razón seno A = ½ en un triángulo
rectángulo, el 41% de los estudiantes escogen el triángulo cuya razón ½ representa el coseno
A, aplicando erróneamente la definición de la razón seno A. Trabajando con valor numérico
5
2
52


3 , en este caso
cancelan inapropiadamente el denominador por ejemplo 3 3 3 3
5
2
52


3 3 .
cancelan los dos radicales en ambos denominadores, siendo lo correcto 3 3 3 3
Al simplificar una identidad trigonométrica asumen que cos A= sec A
En la estadística se pudo notar que en un ejercicio de probabilidad conjunta suman las
probabilidades de los eventos en vez de multiplicarlas. Al calcular una probabilidad consideran
como espacio muestral solo a los elementos favorables.
33
3
En Cálculo al derivar una función como f ( x)  5x  10 x obtienen como respuesta 15x+10x,
dejando ver que sólo derivan el primer término y lo derivan mal porque no operan el exponente
31
11
2
de la variable. El proceso correcto sería f ´(x)  5(3) x  10(1) x  15x  10 .
Al calcular para qué valores es discontinua una función racional, eligen unos que no anulan el
denominador. Al evaluar el límite en una función racional, que tiene un factor repetido en el
numerador y denominador sustituyen directamente en vez de factorizar el numerador y luego
cancelar. Al calcular el límite de una función racional confunden el valor del límite con el valor al
que tiende la variable.
En conclusión, en el Nivel Medio de la Modalidad General, el dominio con menor porciento de
respuesta correcta fue el de Cálculo seguido del Trigonométrico. Los porcientos más bajos de
desempeño en relación a los niveles de complejidad se presentan en el nivel 2 tanto de Cálculo
como de Álgebra, o sea, los estudiantes presentan dificultades al desarrollar ejercicios de estos
dominios que involucran uno o dos procesos. También en el nivel 3 del dominio Trigonométrico,
muestran dificultades para resolver problemas.
Los estudiantes mostraron tener menor dominio en los contenidos algebraicos como son:
ecuaciones e inecuaciones, relaciones y funciones y en límites y derivadas del Cálculo.
34
IV. Nivel Medio: Modalidad Técnico
Profesional y Artes.
4.1. Puntaje Promedio en Las Pruebas Nacionales de Matemática 2015
A continuación se presentan los puntajes promedios obtenidos en las pruebas nacionales de
Matemática en la primera y segunda convocatoria del nivel medio en su modalidad técnicoprofesional.
Tabla No. 4.1
Promedio de puntajes y total de estudiantes examinados en las
Pruebas Nacionales de Matemática, por Convocatoria en el Nivel
Medio Modalidad Técnico Profesional y Artes en el 2015
Nivel Medio Modalidad Técnico Profesional y Artes
Convocatorias
Promedio de puntajes
Total de examinados
Primera
17.47
18,585
Segunda
16.21
6,429
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad.
Como se observa en la tabla, el puntaje promedio obtenido en la primera convocatoria es
superior al obtenido en la segunda pero en ambos casos es bajo.
4.2. Porcentajes de respuestas correctas e incorrectas por dominios
La prueba nacional de matemática de media técnico-profesional cuenta con 45 ítems en cada
cuadernillo y se utilizan dos cuadernillos distintos en cada convocatoria. La mayor cantidad de
ítems corresponde al dominio de Algebra con el 42% de la prueba total, como se puede ver en
la tabla siguiente.
35
Composición de la prueba de matemática y porcentajes de respuestas
correctas e incorrectas , en ambas convocatorias de las Pruebas
Nacionales 2015, en el Nivel Medio Modalidad Técnico-Profesional y
Artes
Tabla No. 4.2
Ítems
%
en Prueba
%
RC
%
RI
1-Lógica y Conjunto
32
17.88
49.35
50.31
2-Algebra
75
41.90
45.34
54.23
3-Geometría
32
17.88
48.10
51.47
4-Trigonometría
20
11.17
42.66
56.67
5-Estadística y Probabilidad
20
11.17
62.53
37.21
Total
179
100.00
Dominio
RC= respuestas correctas; RI= respuestas incorrectas
Fuente: Equipo de estadística. Dirección de Evaluación de la Calidad.
Gráfico 4.1
Porcentajes de respuestas correctas e incorrectas por cada uno de los
dominios en la Primera y Segunda Convocatoria de las Pruebas Nacionales
2015 de Matemática, nivel medio modalidad técnico-profesional
60.00
Título del eje
50.00
40.00
30.00
20.00
10.00
0.00
2.- Algebra
3.- Geometría
%RC
1.- Lógica y
Conjunto
49.35
48.10
4.Trigonometría
42.66
5.- Estadística
y Probabilidad
62.53
45.34
%RI
50.31
54.23
51.47
56.67
37.21
RC= respuestas correctas; RI= respuestas incorrectas
36
Según muestra la tabla No. 4.2 y el gráfico inmediatamente anterior, el dominio que tuvo el
mayor porcentaje de respuestas correctas fue el de Estadística y Probabilidad, con 62.53%
seguido por el de Lógica y Conjuntos con un 49.35; el dominio que tuvo mayor porciento de
respuestas incorrectas fue Trigonometría con un 56.67%. A excepción de Estadística todos los
demás dominios tuvieron un porciento de respuestas correctas por debajo de 50%.
Tabla No. 4.3
Composición de la prueba y porcientos de respuestas correctas
por dominios y nivel de complejidad en las Pruebas Nacionales de
Matemática 2015, Nivel Medio Modalidad Técnico-Profesional.
Matemática Nivel Medio
Modalidad Técnico
Profesional y Artes
Cantidad de
Porcentajes
ítems
Respuestas
Cantidad Proporción
según el
Correctas por nivel
de
en
nivel de
de complejidad
ítems
la prueba
complejidad
/dominio
(%)
1
2
3
1
2
3
Lógica y Conjunto
32
17.88
15
12
5
51.55 51.06 38.67
Algebra
75
41.90
25
31
19
48.53 45.21 41.37
Geometría
32
17.88
14
15
3
53.23 42.75 50.96
Trigonometría
20
11.17
5
8
7
39.75 45.54 41.45
Estadística y Probabilidad
20
11.17
6
9
5
62.59 69.11 50.61
Total
179
100.00
65
75
39
Fuente: Equipo de estadística Dirección de Evaluación de la Calidad.
La tabla No. 4.3 muestra la distribución de ítems evaluados en las pruebas por niveles de
complejidad según el dominio, así como también el porciento de respuestas correctas en cada
nivel.
En el nivel de complejidad 1, el dominio que tiene mayor porciento de respuestas correctas es
el de Estadística y Probabilidad con un 62.59, o sea, que aproximadamente el 63% de los
estudiantes pudieron definir conceptos estadísticos y de probabilidad e identificar datos,
expresiones y notación estadística.
En el nivel de complejidad 2 el dominio de mayor porciento de respuestas correctas fue
Estadística y Probabilidad con un 69.11%. Esto deja claro que más de la mitad de los
estudiantes contestaron correctamente los ítems sobre clasificar objetos estadísticos, procesar
datos en tablas y gráficos estadísticos y con probabilidad simple, describir características y
propiedades.
En el nivel de complejidad 3 el dominio de mayor porciento de respuestas correctas es el de
Geometría con un 50.96%. Los estudiantes fueron capaces de resolver ejercicios geométricos
que involucran más de dos operaciones o procesos, de resolver problemas con figuras
geométricas relacionando sus características y propiedades haciendo conexiones con otras
áreas.
37
4.3. Descripción de los ítems que resultaron fáciles y los que resultaron
difíciles en las Pruebas Nacionales de Matemática en Media
Técnico- Profesional y Artes.
Dominio Lógico Conjuntista
Fáciles: Escribir en lenguaje coloquial proposiciones dadas en lenguaje lógico-simbólico.
Determinar el producto cartesiano entre dos conjuntos dados por extensión.
Difíciles: Resolver problemas aplicando intersección entre conjuntos y leyes de Morgan. Dado
un gráfico que representa relaciones entre conjuntos, determinar la veracidad o falsedad de
expresiones dadas en lenguaje conjuntista, que involucran unión e intersección entre conjuntos.
Determinar si una forma proposicional que involucra negaciones e implicación es una
tautología, contradicción, contingencia o equivalencia lógica. Dada una expresión en lenguaje
conjuntista que incluye intersección y unión entre conjuntos, identificar la gráfica que le
corresponde. Calcular los valores de verdad de las proposiciones simples para que una forma
argumental que involucra negación e implicación, tenga valor de verdad falso. Dado un gráfico
que representa el resultado de una operación entre dos conjuntos, identificar la operación.
Dados varios conjuntos expresados por comprensión, con proposiciones relacionadas con
números y figuras geométricas, identificar cual representa un conjunto vacío. Identificar el
gráfico que represente el producto cartesiano de dos conjuntos dados.
Dominio Algebraico
Fáciles: Dada la fórmula para encontrar el inverso de un número complejo, calcular para un
complejo dado en la forma binómica. Traducir al lenguaje cotidiano una expresión polinómica
que contiene las operaciones de producto y suma. Dado el gráfico de un complejo
representado en un plano gaussiano, identificar el complejo que le corresponde en su forma
binómica. Resolver problemas que se traducen a ecuaciones de primer grado. Dado el
complejo en forma binómica, identificar el gráfico que le corresponde en un plano Gaussiano.
Difíciles: Calcular la pendiente de una recta dada su ecuación. Calcular la ecuación de la recta
que pasa por dos puntos dados. Calcular la pendiente de rectas dados dos puntos de ellas.
Identificar términos fraccionarios de una lista dada. De varias gráficas identificar la que sea
simétrica al origen. Determinar las raíces de una ecuación cuadrática dada en la forma
ax 2  bx  c  0, con a  1 . Expresar en forma de potencia una expresión radical de la forma
n
a p  b q , y dada en forma de potencia llevarla a la forma radical. Identificar un polinomio que
no puede ser factorizado usando números enteros. Evaluar un polinomio cuando los valores
dados de las variables son fraccionarios. Dividir dos monomios con tres variables iguales en
cada uno y con exponentes enteros positivos. Dividir dos expresiones algebraicas fraccionarias.
Dada una expresión algebraica con exponentes negativos, escribir una equivalente con
exponentes positivos. Identificar la ecuación de la función que corresponde a una parábola
graficada en un plano cartesiano. Dado un problema, identificar el modelo que no conduce a su
solución.
38
Identificar una expresión en forma de cociente que tiene un solo término. Calcular el resultado
del producto de un trinomio por un binomio. Determinar el valor que puede tomar b en
un trinomio dado en la forma ax  bx  c, con a  1 , y conocidos a y c, para que pueda
factorizarse en dos binomios de primer grado. Dado un intervalo en la recta numérica,
identificar la desigualdad que la genera. Identificar fracciones algebraicas equivalentes. Evaluar
polinomios con coeficientes enteros y fraccionarios donde los valores de las variables son
fraccionarios. Resolver y graficar una desigualdad con y sin valor absoluto. Ordenar polinomios
con relación a una variable.
2
Dominio Geométrico
Fáciles: Determinar la veracidad o falsedad de proposiciones que implica traslaciones,
rotaciones y reflexiones de figuras dadas en cuadrículas. Determinar la altura de objetos
alineados conocidos las alturas y las distancias que los separan, evidenciándose en la figura
proporcionalidad entre los objetos. Determinar paralelismo de objetos ubicados en calles
paralelas. Identificar transformaciones geométricas de figuras en una cuadrícula.
Difíciles: Calcular la longitud de un lado de un triángulo en el plano coordenado, dadas las
coordenadas de los puntos de sus vértices. Identificar una región convexa de una figura
geométrica dada. Calcular un lado de una figura semejante con otra, conocido un lado y la
razón de semejanza entre los lados del triángulo, sin contemplar la figura. Identificar figuras
semejantes en un gráfico formado por rectas paralelas y secantes. Calcular las constantes de
proporcionalidad dados los valores de las partes proporcionales entre figuras semejantes.
Calcular el área de un cuadrado, cuando hay que calcular el lado de un triángulo contiguo
usando el teorema de Pitágoras. Identificar dos triángulos semejantes localizados entre dos
rectas paralelas cortadas por dos secantes. Verificar mediante el cálculo de la pendiente (m) si
tres puntos son colineales. Calcular el valor de un lado de un triángulo usando el teorema del
coseno.
Dominio Trigonométrico
Fáciles: No hay evidencia de ítems fáciles en este dominio.
Difíciles: Calcular valor numérico de expresiones trigonométricas con funciones de ángulos
notables. Calcular un lado de un triángulo usando la ley de coseno.
Dominio Estadístico-Probabilístico
Fáciles: Calcular la probabilidad de ocurrencia de un evento simple. Identificar un gráfico de
pastel que corresponda a una distribución porcentual. Identificar la categoría que representa la
mediana de un conjunto de datos conocidas sus frecuencias, dadas en un gráfico de barras.
Calcular las probabilidades de varios eventos para elegir el evento más probable. Interpretar
informaciones a partir de un polígono de frecuencias.
Difíciles: Identificar la muestra estudiada de una población dada.
39
4.4. Análisis de los ítems que resultaron más fáciles y más difíciles
Se presenta un análisis pedagógico de algunos de los ítems que resultaron más difíciles en
función de los errores que cometen los estudiantes, fundamentado en tres categorías:
contenido del ítem, operación cognitiva y contexto. A continuación se modelan con ejemplos
algunos casos:
4.4.1 Análisis pedagógico de los ítems que resultaron más fáciles
Ejemplo 1. Una familia distribuye su presupuesto de la siguiente manera; pago de los colegios
de los hijos 25%; alimentación 40%; servicios 20% y para imprevistos 15%. ¿Cuál de los
siguientes gráficos representa aproximadamente esa distribución?
Información del ítem
Respuesta correcta: A
Dominio: Estadístico
Contenido: Interpretación de gráficos estadísticos
Nivel taxonómico: 2
Dificultad del ítem: aproximadamente el 80% de los estudiantes contestó correctamente el
ítem, por lo que este ítem resultó fácil.
Operación cognitiva: Para contestar correctamente el ítem el estudiante tenía que comparar
el tamaño de cada sección del gráfico circular con el porcentaje asignado a cada categoría, y
estimar su correspondencia para identificar el gráfico que representa la situación.
40
Reflexión pedagógica:
Una de las razones que pudiera justificar la facilidad de este ítem es que el contexto es familiar
porque se relaciona con el presupuesto de la familia. Se recomienda relacionar la estadística
con situaciones cotidianas.
4.4.2 Análisis pedagógico de los ítems que resultaron más difíciles
Ejemplo 1. ¿A cuál de las siguientes funciones corresponde el gráfico dado a continuación?
A)
f ( x)  ( x  2)2
f ( x) 
B)
1 2
x
2
C) f ( x)  3x
f ( x) 
D)
2
3
x2
Información del ítem
Respuesta correcta: B
Dominio: Algebraico.
Contenido: La función cuadrática,
Nivel taxonómico: 2
.
A
34.67
B
19.44
C
26.74
D
19.94
41
Dificultad del ítem: La opción B es la correcta y el 19.44% de los estudiantes contestó
correctamente el ítem, por lo que este ítem resultó difícil. La opción A la elige la mayoría con un
34.67%, pero la gráfica de esta función es una parábola movida horizontalmente dos unidades
a la izquierda del vértice. La opción C la elige el 26.74% y la gráfica de esta función es una
parábola que tiene su vértice en el origen del plano pero abre hacia abajo, y la opción D, que es
la menos coherente la elige el 18.94%, su gráfica no corresponde a una parábola.
Operación cognitiva: Para contestar correctamente el ítem los estudiantes tienen que hacer
corresponder una de las funciones dadas en las opciones con la gráfica dada. Para esto
generalmente se analizan el valor de a que es el coeficiente de la expresión cuadrática y las
coordenadas del vértice V(h, k) de la función.
Reflexión pedagógica: Este tipo de ejercicios es útil para que los alumnos puedan asignar
las características básicas de la gráfica de una función partiendo de su ecuación y partiendo de
los parámetros generales a y V(h, k) puedan hacer la transferencia a los diferentes registros de
representación (algebraico, gráfico) con facilidad. Además para que asuman que en cualquier
registro que se presente la información representa el mismo objeto matemático, o sea, la
función representa lo mismo que el gráfico pero escrito en otro formato.
Ejemplo 2. ¿Cuál es la ecuación de la recta que pasa por los puntos A(1,5) y B(5,3)?
1
11
y  x
2
2
A)
1
11
y  x
2
2
B)
y
1
11
x
2
2
y
1
11
x
2
2
C)
D)
Información del ítem
Respuesta correcta: A
Dominio: Algebraico
Contenido: Ecuación de la recta
Nivel taxonómico: 2
42
.
A
19.52
B
20.24
C
46.51
D
13.28
Dificultad del ítem: La opción correcta es la A y aproximadamente el 20% de los estudiantes
la eligió, por lo que este ítem resultó difícil. La Opción B fue elegida por el 20.24% porque
hicieron incorrecta la transposición de términos. La opción C la eligió el 46.51% porque
multiplicaron mal números con signos diferentes. La opción D la eligió el 13.28% porque
tuvieron mal manejo de los signos en el proceso de transposición de términos. Este ítem se
presenta en un contexto matemático no asociada a ninguna situación cotidiana lo que lo hace
más abstracto y difícil.
Operación cognitiva: Para contestar correctamente el ítem el estudiante tenía que calcular la
pendiente de la recta que pasa por los puntos dados y luego aplicar la ecuación en su forma
punto y pendiente y luego despejar la variable y dejarla en la forma estándar.
Reflexión pedagógica: La dificultad del ítem puede estar relacionada con el contexto abstracto
en el que se presenta y por la cantidad de procesos algebraicos que involucra. Se sugiere
indagar sobre la enseñanza de este contenido en Segundo Grado porque casi todos los ítems
de la ecuación de la recta en diferentes formatos (implícita, explicita y general) resultaron
difíciles.
4.5. Contenidos de mayor dificultad de acuerdo a errores cometidos en
los ítems
Al resolver problemas que involucra distribuir el total de elementos de un conjunto en conjuntos
más pequeños con intersección, asumen la intersección para uno de los conjuntos y no para el
otro; por ejemplo: “del total de 15 estudiantes, 8 están en baile y 3 están en baile y canto,
¿cuántos están en canto? Primero como 3 estudiantes están en baile y canto, están en la
intersección de los dos conjuntos; luego como hay ocho en baile faltan 5 para ese conjunto y
luego como son quince estudiantes faltan 7 que están sólo en canto
Por tanto hay 10 estudiantes en canto.
43
Con relación al Álgebra, en una división de monomios con las partes literales iguales suman los
exponentes.
3 pq 3
3 7
2 4
Por ejemplo, si se le pide que dividan p q obtienen como respuesta 3 p q siendo lo correcto
3
pq . Al escribir una expresión que tiene exponentes negativos de forma que sus exponentes
queden positivos, el 53% de los alumnos cambian el signo dejando la expresión igual, por
3
3
ejemplo cambian m por m como si fueran iguales. Se recomienda aclarar el efecto del signo
negativo en el exponente como sigue
m3 
1
m3 . Al dividir dos expresiones racionales dan como
3a
m
3a 2
resultado el recíproco del resultado, por ejemplo al dividir
a
mp obtienen p cuando lo correcto
p
es a
De varias figuras dadas en el plano, se pide identificar cuál es simétrica respecto al origen y
eligen una parábola como la siguiente
, mostrando poco dominio para identificar si dos
o más puntos son simétricos respeto al origen ignorando que por cada punto (x, y) existe otro (x,-y). Al expresar en lenguaje algebraico la expresión “se le resta 20,000 al duplo de una
cantidad” lo escriben como 20,000-2x, siendo la forma correcta 2x-20,000. Al simplificar una
expresión de la forma 2x-3x+4x, obtienen -3x como respuesta,
operando incorrectamente
cantidades con signos contrarios. Al hallar la ecuación de la recta en la forma y = mx + b, que
pasa por el punto (3,2) y m=1, escriben la ecuación como y=3x+2, usando los valores del punto
de forma incorrecta y omitiendo el valor de la pendiente.
En este caso lo correcto es y-2=1(x-3) de donde se reduce a y=x-1 que es la ecuación correcta.
Por otro lado al calcular la pendiente de la recta que une dos puntos dados lo hacen inverso
dividiendo la diferencia en x entre la diferencia en y, obteniendo la pendiente recíproca de la
que se busca. Al resolver una inecuación cuyo coeficiente de la variable es negativo no
invierten el signo de la desigualdad. Al elegir el intervalo solución de la inecuación x  5 ,
eligen los números a la derecha de -5 en la recta numérica.
44
En Geometría, más de la mitad de los estudiantes fallaron al calcular la constante de
proporcionalidad entre dos segmentos proporcionales dados. Se les pidió que calcularan el
área del cuadrado que se forma con uno de los catetos de un triángulo rectángulo del cual se
conoce la hipotenusa y el otro cateto; en este problema sólo bastaba aplicar el teorema de
Pitágoras para hallar el otro cateto y luego ese valor al cuadrado, que es el área pedida; la
mayoría no pudo contestar correctamente este ítem cuya gráfica se modela a continuación
En lo referente a la trigonometría fallaron al calcular el valor numérico de una expresión
trigonométrica pues asignan valores equivocados a las razones trigonométricas. Al calcular el
lado faltante de un triángulo donde se puede aplicar la ley de coseno, escogen la opción que
más se acerca a la suma de las medidas de los lados dados.
En estadística y probabilidad la mayoría no pudo identificar el concepto de muestra estadística.
En general, los dominios que mostraron más debilidades son Trigonometría y Álgebra. En
Trigonometría mostraron dominio de las definiciones de las razones trigonométricas en el
triángulo rectángulo, pero la mayoría falló en aplicar las leyes de seno y coseno para resolver
triángulos y en valor numérico de expresiones trigonométricas con ángulos agudos. En Álgebra,
se destacan debilidades en la factorización de polinomios, simplificación de expresiones
racionales, definir término fraccionario, ecuaciones e inecuaciones y en relaciones y funciones.
El tema de Álgebra que más debilidades presentó fue el de la ecuación de la recta y la función
cuadrática en todas sus formas.
Con relación a los niveles de complejidad, las mayores debilidades estuvieron en el nivel 3 de
Lógica y Conjuntos, Álgebra y Trigonometría, lo que significa que tienen dificultades para
resolver problemas aplicando esos contenidos. Además en Trigonometría tuvieron dificultades
para desarrollar ejercicios que demandan uno o dos procesos que corresponden al nivel de
complejidad 2.
45
Conclusión
A continuación se presentan en forma resumida los hallazgos más relevantes.
Las Pruebas Nacionales de Matemática indican los logros de aprendizaje alcanzados por los
estudiantes en ésta área. En los análisis presentados en este informe se visualiza que
enfrentamos grandes retos al respecto. Entre los retos están: aumentar el promedio de puntaje
y el porcentaje de respuestas correctas por dominio en todos los grupos evaluados; mejorar el
desempeño de los estudiantes en los niveles de complejidad más altos, o sea, en la habilidad
de resolución de problemas y emprender acciones concretas para mejorar el dominio de temas
específicos con mayores dificultades señalados en este informe. Como en educación los
cambios no ocurren bruscamente, sería realista proponerse que en las próximas pruebas
nuestros estudiantes alcancen más del 50% de respuestas correctas en todos los dominios.
Cabe recordar que los dominios con más debilidades para el Octavo Grado fueron el
Algebraico, Numérico y Métrico; para el Tercer Ciclo de adultos Mediciones, Geometría y
Números; en el Nivel Medio General el Cálculo seguido del Trigonométrico y el Algebraico, y
en Técnico y Artes los dominios Trigonométrico y Algebraico, cuyos porcientos de respuestas
correctas no alcanzaron el 50%.
Con relación a los temas específicos con mayores debilidades están las operaciones con
números racionales, áreas y volúmenes, las ecuaciones e inecuaciones, geometría de
coordenadas y teorema de Pitágoras, ecuación de la recta, relaciones y funciones, función
cuadrática, límite y derivadas, razones trigonométricas, leyes de seno y coseno.
Desde la Dirección de Evaluación del MINERD se recomienda que todos los actores de la
comunidad educativa usen estos resultados en la mejora de los aprendizajes de los
estudiantes. Específicamente las Direcciones Generales y de los Niveles, Regionales de
Educación, Distritos Educativos y los centros educativos deben organizar espacios de lectura y
reflexión de este documento junto con el Informe de Centro con los docentes del área, para
elaborar un diagnóstico, proponerse metas y elaborar planes de mejora que apunten al logro de
esas metas.
Por otro lado, las instancias correspondientes del MINERD, deben elaborar materiales
didácticos-metodológicos que apunten a diferentes estrategias de abordaje de los dominios y
temas señalados como más emergentes en este informe y la resolución de problemas, con el
fin de socializarlos en talleres con los docentes y dar seguimiento a los docentes en la
aplicación de estas estrategias en el aula.
Además se orienta a que las instituciones de formación inicial y capacitación continua de los
docentes, usen estos resultados para revisar las estrategias que se están aplicando en la
enseñanza- aprendizaje de los contenidos matemáticos que resultaron más débiles. El
MINERD, a través del INAFOCAM puede identificar docentes con más necesidades de
capacitación.
46
En el seguimiento que se da a los centros educativos y los docentes, incluir un indicador sobre
“el uso que dan a los resultados de las evaluaciones nacionales e internacionales” para la
mejora.
Las instancias correspondientes deben diseñar clases modelos con los temas que los alumnos
dominan poco para desarrollar con los docentes estrategias didácticas válidas. Estas clases se
pueden modelar en programas radiales y televisivos educativos como Radio Educativa
Dominicana y a través de la Tecnología. También deben revisar los enfoques de enseñanza
aprendizaje, los textos escolares, los aspectos didácticos, metodológicos y los recursos
usados en el proceso de enseñanza aprendizaje de estos dominios y proponer ajustes.
Se recomienda que los docentes sean entrenados en el uso de estrategias de resolución de
problemas como Aprendizaje Basado en Problemas (ABP), para que los estudiantes alcancen
niveles avanzados de razonamiento.
47
Anexos
Tabla Anexo No. 1
Niveles
1
Descripción de los niveles taxonómicos en los procesos
cognitivos de Matemática
Descripción
Se refiere a procesos que implican el conocimiento y la comprensión de
hechos y datos, recordar información, definir un concepto, identificar
elementos
-Define conceptos matemáticos.
-Reconoce el lenguaje matemático, modelos, diagramas, símbolos para representar
Conceptos e ideas matemáticas.
-Identifica elementos, expresiones y figuras matemáticos
Se refiere a procesos que implican la comprensión de relaciones simples e
interacciones de varios elementos, la construcción de significados a partir de
elementos dados, el establecer conexiones.
2
-Establece relaciones entre figuras y elementos matemáticos
-Resuelve ejercicios matemáticos que involucren hasta dos procesos matemáticos
-Clasifica objetos matemáticos
- Establece relaciones con objetos matemáticos
-Opera con objetos matemáticos
-Describe procesos matemáticos
-Describe propiedades entre elementos de objetos matemáticos
-Establece conexiones entre objetos matemáticos
53
Se refiere a aplicar principios, resolver problemas, analizar los elementos que
intervienen en una situación, sus relaciones e implicaciones.
3
-Resuelve ejercicios que involucran más de dos procesos matemáticos
-Selecciona la información necesaria para resolver problemas matemáticos.
-Usa esquemas, tablas, gráficas, dibujos, para resolver problemas matemáticos.
-Evalúa la validez de los resultados de un problema matemático cotidiano.
- Describe el proceso utilizado al resolver problemas matemáticos.
-Planifica, escoge y aplica métodos y estrategias adecuadas para resolver
problemas matemáticos.
-Plantea y resuelve problemas donde haya que calcular e inferir datos
-Aplica propiedades en la resolución de problemas matemáticos
-Hace demostraciones matemáticas
-Evalúa la pertinencia de la solución de un problema
-Resuelve problemas que involucra conexiones entre la matemática y otras áreas.
48
Tabla Anexo No. 2
Descripción de los dominios en Octavo Grado
Dominio
Numérico
Algebraico
Geométrico
Métrico
Estadístico
Descripción
Trata sobre el conjunto de los números racionales e irracionales en sus
diferentes formas de representación, las operaciones de adición,
sustracción, multiplicación, división, potenciación y radicación, las
propiedades de los números reales y sus aplicaciones en la resolución de
problemas del entorno.
Se fundamenta en el manejo e interpretación del lenguaje algebraico,
mediante el uso de constantes y variables, enfatizando la traducción
de un lenguaje al otro y viceversa, así como también a la evaluación de
expresiones algebraicas, la resolución de ecuaciones e inecuaciones y la
resolución de problemas de aplicaciones.
Abarca los conceptos básicos de geometría sobre localización de puntos en
el plano cartesiano, transformaciones geométricas como traslación,
rotación, reflexión y simetrías, embaldosado del plano y aplicación del
concepto de fractal. Se estudian los conceptos básicos de los cuerpos
geométricos redondos y sus propiedades.
En este tema se estudian las diferentes estrategias para calcular el área y el
volumen de la superficie de los cuerpos redondos: cono, cilindro y esfera y
la resolución de problemas de aplicaciones prácticos.
Trata sobre recolección, organización y análisis de datos provenientes de
poblaciones y/o muestras, mediante tablas, distribuciones de frecuencias,
construcción e interpretación de diferentes tipos de gráficos.
Además se estudia la probabilidad de ocurrencia de sucesos obtenidos al
azar, analizando tablas, diagramas en árbol, realizando experimentos y
simulaciones para resolver problemas prácticos.
Tabla Anexo No. 3
Dominio
Numérico
Algebraico
Geométrico
Métrico
Estadístico
Totales
Porcentajes
Tabla de especificaciones para Octavo
Grado
Cantidad de ítems
por dominio
13
8
7
6
6
40
100%
Niveles de complejidad de los ítems
1
2
3
3
3
3
1
2
12
30%
6
3
2
3
2
16
40%
4
2
2
2
2
12
30%
49
Tabla Anexo No. 4
Descripción de los dominios en Tercer Ciclo de Adultos
Dominio
Numérico
Descripción
Se estudian los números enteros y racionales en sus diferentes formas de
presentación a través de las operaciones aritméticas de adición, sustracción,
multiplicación, división, potenciación y radicación, orientados en el uso de las
propiedades y los cálculos comerciales y/o financieros en la resolución de
problemas prácticos.
Se estudian los conceptos básicos de geometría como rectas, ángulos, planos,
teoremas, el teorema de Pitágoras y sus aplicaciones, la localización de
Geométrico puntos y figurasen el plano cartesiano, con o sin material cuadriculado, las
generalidades y características de los cuerpos geométricos prisma, pirámide,
cilindro, cono y esfera y problemas de aplicación.
Métrico
Estadístico
Estudia las estrategias para calcular el área de la superficie y el volumen de
Prismas y pirámides de diferentes bases. Además, cómo calcular el área de la
superficie y el volumen de conos, cilindros rectos y esfera. Se incluyen
estrategias para la resolución de problemas de aplicaciones
Prácticas.
Trata sobre recolección, organización, análisis e interpretación de datos
provenientes de poblaciones y/o muestras, mediante tablas o gráficos.
Además se estudia la probabilidad de ocurrencia de sucesos obtenidos al azar,
se realizan experimentos y simulaciones de eventos aleatorios, y se resuelven
problemas de aplicación.
Tabla Anexo No. 5
Dominio
Tabla de especificaciones para Tercer Ciclo de Adultos
Cantidad de ítems
por dominio
Niveles de complejidad de los ítems
1
2
3
Numérico
13
5
5
3
Geométrico
11
3
5
3
Métrico
8
2
4
2
Estadístico
8
2
4
2
Totales
40
12
18
10
100%
30%
45%
25%
Porcentajes
50
Tabla Anexo No. 6
Descripción de los dominios en Media Modalidad General
Dominio
Descripción
Trata sobre el uso correcto del lenguaje lógico y conjuntista a través del estudio de
proposiciones, tipos de razonamientos, demostraciones, construcción de diferentes tipos
de pruebas, conceptos básicos de la teoría de conjuntos, relaciones
y operaciones entre conjuntos, mediante el uso adecuado de la simbología y las
aplicaciones a la resolución de problemas.
Lógico
conjuntista
Trata sobre el estudio de las expresiones algebraicas, el uso adecuado del lenguaje
matemático, las operaciones fundamentales con expresiones algebraicas, las ecuaciones
e inecuaciones y los sistemas en una y dos variables de primer y segundo grados.
Estudia también las relaciones y funciones, el análisisde gráficas de funciones, las
ecuaciones exponenciales y logarítmicas, los números complejos en forma binómica y par
ordenado, matrices y determinantes y sus operaciones fundamentales y el binomio de
Newton, las sucesiones y series y sus aplicaciones a la resolución de problemas
prácticos.
Algebraico
Geométrico
Trigonométrico
Estadístico
Cálculo
Estudia los conceptos fundamentales de la geometría plana como punto, recta, plano,
ángulos, polígonos, su clasificación y la aplicación de postulados y teoremas
fundamentales sobre los mismos del Incluye además, el estudio del razonamiento y las
diferentes formas de demostración, los cuerpos geométricos, áreas y volúmenes.
Comprende la trigonometría plana, las razones, funciones e identidades y ecuaciones
trigonométricas, sus aplicaciones para resolver problemas del mundo real. Los números
complejos en forma trigonométrica, operaciones y propiedades
Estudia la recolección, organización y análisis de datos estadísticos, la probabilidad
teórica y experimental y sus operaciones a través de las reglas que las rigen y sus
aplicaciones en la vida cotidiana. Estudia además el análisis combinatorio y sus
propiedades.
Estudia los conceptos básicos sobre límites, operaciones y propiedades, el uso de la
derivada y sus aplicaciones para resolver problemas sobre máximos y mínimos de una
función, así como también las razones de cambio relacionadas con situaciones del mundo
real.
Tabla Anexo No. 7
Dominio
Lógico conjuntista
Algebraico
Geométrico
Trigonométrico
Estadístico
Cálculo
Totales
Porcentajes
Tabla de especificaciones para Media Modalidad
General
Cantidad de
ítems por
dominio
6
18
9
6
7
4
50
100%
Niveles de complejidad de los ítems
1
2
3
3
6
4
1
2
1
17
34%
2
8
3
2
2
2
19
38%
1
4
2
3
3
1
14
28%
51
Tabla Anexo No. 8
Descripción de los dominios en Media Modalidad Técnico
Profesional y Artes
Dominio
Lógico
conjuntista
Algebraico
Geométrico
Trigonométrico
Estadístico
Descripción
Trata sobre el uso correcto del lenguaje lógico y conjuntista a través del
estudio de proposiciones, tipos de razonamientos, demostraciones,
construcción de diferentes tipos de pruebas, conceptos básicos de la teoría
de conjuntos, relaciones y operaciones entre conjuntos, mediante el uso
adecuado de la simbología y las aplicaciones a la resolución de problemas.
Trata sobre el estudio de las expresiones algebraicas, el uso adecuado del
lenguaje matemático, las operaciones fundamentales con expresiones
algebraicas, las ecuaciones e inecuaciones lineales y cuadráticas. Estudia
también las relaciones y funciones lineales y cuadráticas con análisis de
gráficas, la pendiente y ecuación de la recta, los números complejos en
forma binómica y par ordenado y aplicaciones a resolución de problemas.
Estudia los conceptos fundamentales de la geometría plana como punto,
recta, plano, ángulos, polígonos, su clasificación y áreas. Incluyendo la
aplicación de postulados y teoremas fundamentales en demostraciones
geométricas. Se estudia además las transformaciones geométricas
isométricas: traslaciones, reflexiones y rotaciones.
Comprende la trigonometría plana, las razones, funciones e identidades
trigonométricas fundamentales, sus aplicaciones para resolver problemas
del mundo real. La ley del seno y del coseno y sus aplicaciones.
Estudia la recolección, organización y análisis de datos estadísticos, las
medidas de tendencia central, correlación y dispersión. La probabilidad
teórica y experimental y sus operaciones a través de las reglas que las
rigen y sus aplicaciones en la vida cotidiana.
Tabla Anexo No. 9
Dominio
Tabla de especificaciones para Media Modalidad Técnico
Profesional y Artes
Cantidad de
ítems por
dominio
Niveles de complejidad de los ítems
1
2
3
Lógico conjuntista
8
3
3
2
Algebraico
19
6
8
5
Geométrico
8
4
2
2
Trigonométrico
5
1
2
2
Estadístico
5
1
2
2
Totales
45
15
17
13
100%
33%
38%
29
Porcentajes
52