Programación Estructurada

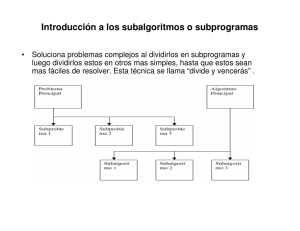
Introducción a los subalgoritmos o subprogramas
•
Soluciona problemas complejos al dividirlos en subprogramas y
luego dividirlos estos en otros mas simples, hasta que estos sean
mas fáciles de resolver. Esta técnica se llama “divide y vencerás” .
Introducción a los subalgoritmos o subprogramas
•
Se dice que el programa principal invoca al subprograma, el
subprograma ejecuta la tarea y luego devuelve el control al
programa.
Introducción a los subalgoritmos o subprogramas
• Un programa puede llamar a su ves a sus
propios subprogramas
COMUNICACIÓN CON SUBPROGRAMAS: Parámetros
La lista de parámetros esta compuesta de los nombres de
los mismos y del tipo de datos que representan, los del
mismo tipo se separan con comas "," y cada tipo diferente
se separa con punto y coma ";".
Procedure Ejemplo(a, b : Integer; c, d : String);
Para llamar a un procedimiento que utiliza parámetros se
pueden utilizar como tales otras variables o constantes,
siempre y cuando sean del mismo tipo que los declarados.
Ejemplo(1, 2, 'Hola', 'Adios');
Funciones y Procedimientos: Subprogramas
Los parámetros
•
Son canales de comunicación para pasar datos ente programas y subprogramas en
ambos sentidos.
•
Estan asociados a variables. constantes, expresiones, etc., y por tanto, se indican
mediante los correspondientes identificadores o expresiones.
•
Se utilizan en la llamada o invocación al subprograma se denominan parámetros
actuales, reales o argumentos, y son los que entregan la información al subprograma.
•
Los parámetros que la reciben en el subprograma se denominan parámetros formales o
ficticios y se declaran en la cabecera del subprograma.
•
Los parámetros son opcionales y si no se necesitan no se deben usar. Para utilizarlos
es necesario declararlos: PROCEDURE nombre (lista de parámetros);
•
En una llamada a un subprograma tiene que verificarse que:
–
–
El número de parámetros formales debe ser igual al de actuales.
Los parámetros que ocupen el mismo orden en cada una de las Listas deben ser compatibles
en tipo.
Ej. Programa que use parametros ..
PROGRAM Parametros;
VAR
Saludo : String;
PROCEDURE Imprime_5 (a : String);
VAR
Contador : Integer;
BEGIN
FOR contador := 1 to 5 DO
{Imprime 5 veces la cadena almacenada }
WriteLn(a);
{en la variable "a", que es la información}
END;
{que llega como parámetro }
BEGIN
Saludo := 'Bienvenidos al programa';
Imprime_5 (Saludo);
{llama al procedimiento Imprime_5, usando como}
{parámetro la variable Saludo }
Imprime_5 ('Fin');
{Utiliza la cadena "fin" como parámetro }
END.
Creación de los procedimientos
1.- Que debe hacer el procedimiento
2.- Declaramos el procedimiento, despues de haber declarado variables y
constantes, antes del cuerpo del programa principal.
PROCEDURE Titulo;
BEGIN
WriteLn ('Programa de Turbo Pascal');
END;
Uso de los procedimientos
Una vez declarado el procedimiento es posible utilizarlo como una instrucción
de Turbo Pascal. Al uso de un procedimiento se le conoce como llamada al
procedimiento.
PROGRAM Procedimientos;
PROCEDURE Titulo;
BEGIN
WriteLn ('Programa de Turbo Pascal');
END;
BEGIN
WriteLn ('Programa ejemplo del uso de procedimientos');
Titulo;
{Llama al procedimiento}
WriteLn;
Titulo;
{Vuelve a llamar al procedimiento}
END;
Variables locales y globales
En Pascal cada
identificador tiene un
campo de acción,
solo dentro de éste
campo es posible
utilizarlo. Ej.: Las
variables, que pueden
ser globales o locales.
PROGRAM Variables;
VAR
Hola : String;
PROCEDURE prueba;
VAR
Adios : String;
BEGIN
{En esta sección si es posible usar la variable Hola}
Adios := 'Adios, que les vaya bien';
WriteLn (Adios);
END;
BEGIN
{En esta sección no se reconoce a la variable Adios}
Hola := 'Hola, bienvenidos al programa';
WriteLn (Hola);
WriteLn (Adios);
{Al compilar el programa se generará un error ya}
prueba;
END.
ÁMBITO: VARIABLES LOCALES Y GLOBALES
Las variables utilizadas en los principales y subprogramas se clasifican en dos
tipos:
· Variables locales.
· Variables globales.
Una variable local es aquella que está declarada y definida dentro de un
subprograma, en el sentido de que está dentro de ese subprograma y es
distinta de las variables con el mismo nombre declaradas en cualquier parte
del programa principal. El significado de una variable se confina al
procedimiento en el que está declarada.
Una variable global es aquellas que está declarada para el programa o
algoritmo principal, del que dependen todos los subprogramas.
La parte del programa/algoritmo en que una variable se define se conoce como
ámbito (scope, en inglés)
Ventajas de variables locales: Hace a los subprogramas independientes, con la
comunicación entre el programa principal y los subprogramas manipulados
estructuralmente a través de la lista de parámetros.
ÁMBITO: VARIABLES LOCALES Y GLOBALES
ÁMBITO: VARIABLES LOCALES Y GLOBALES
Definición de las funciones
Las funciones son, al igual que los procedimientos, un conjunto de sentencias
que se ejecutan constantemente, la diferencia entre éstas y los
procedimientos es que las funciones regresan un valor.
FUNCTION nombre(parámetros) : tipo_de_datos;
FUNCTION Promedio (a, b : Real) : Real; {Promedio de dos números reales}
BEGIN
Promedio := (a + b) / 2;
END;
Uso de las funciones
PROGRAM Funciones;
VAR
X, Y, Z : Real;
Como las funciones devuelven
un valor específico la forma
más usual de utilizarlas es
por medio de asignaciones
de una variable a la
función.
FUNCTION Promedio (a, b : Real) : Real;
{Promedio de dos números reales}
BEGIN
Promedio := (a + b) / 2;
END;
BEGIN
X := 5.89;
Y := 9.23;
Z := Promedio (X, Y);
{Iguala Z al valor devuelto por la función
Promedio}
WriteLn('El promedio de ',X,' y ',Y,' es:
',Z);
END.
Procedimieto HALT
El procedimiento HALT ya se habia revisado anteriormente, pero se tomó
como una instrucción, siendo que es realmente un procedimiento
predefinido de Turbo Pascal que nos permite terminar nuestro programa en
cualquier punto del mismo.
El procedimiento EXIT provoca la salida del procedimiento que se está
ejecutando y nos regresa al lugar de donde fue llamado.
Procedimientos INC y DEC
El procedimiento INC incrementa en 1 el contenido de cualquier variable de
tipo entero, es lo mismo en un programa teclear:
Variable := Variable + 1;
o telcear:
Inc(Variable);
El procedimiento DEC decrementa en 1 el valor de cualquier variable de
tipo entero que se le indique, se usa igual que INC:
DEC (Variable);
Procedimiento versus función
Los procedimientos y funciones son subprogramas cuyo diseño y misión son
similares, sin embargo, existen unas diferencias esenciales entre ellos:
1. Un procedimiento es llamado desde el algoritmo o programa principal
mediante su nombre y una lista de parámetros actuales, o bien con la
instrucción llamar_a (call).
Al llamar al procedimiento se detiene momentáneamente el programa que
se estuviera realizando y el control pasa al procedimiento llamado.
Después de que las acciones del procedimiento se ejecutan, se regresa a
la acción inmediatamente siguiente a la que se llamó.
2. Las funciones devuelven un valor, los procedimientos pueden devolver 0,1 o
n valores y en forma de lista de parámetros.
3. El procedimiento se declara igual que la función, pero su nombre no está
asociado a ninguno de los resultados que obtiene.
Programacion Estructurada
• Los avances tecnológicos no necesariamente están acompañados por
una evolución en las técnicas de construcción de programas.
• Se requieren programas mas complejos y de gran tamaño.
• Diseño Descendente o Diseño Top-Down
• Las técnicas de desarrollo y diseño de programas, que se utilizan en la
programación convencional o lineal, tienen inconvenientes, sobre todo a
la hora de verificar y modificar programas.
• Técnicas que facilitan la la comprensión del programa: Programación
estructurada
• Pioneros de esta metodología: Dijkstra, Warnier, Jackson, Chapin y
Bertini; y de los Lenguajes de Programación Estructurada Niklaus Wirth,
Dennis Ritchie y Kenneth Thompson.
Estructura: Es la descomposición ordenada de las partes de un todo.
Conjunto de elementos interrelacionados que forman un todo.
Programación Estructurada: Consiste en el diseño, escritura y prueba
de un programa, construido con estructura, o sea con una organización
ordenada del todo en partes interdependientes.
Herramientas. Estructuras Básicas. Figuras Lógicas.
Teorema de la Estructura
Aporte de BOHN y JACOPINI (1966). Matemáticamente todo problema puede
resolverse con tres figuras lógicas (secuencia, alternativa y repetitiva o
iterativa).
La programación estructurada se consigue mediante la descomposición en
partes, segmentos, rutinas o subproblemas interdependientes; que pueden
ser considerados como las unidades razonablemente pequeñas, que deben
representar por si mismas un contenido lógico, coherente y completo.
Esta segmentación debe realizarse de lo general a lo particular, organizando
por niveles con grado de detalle creciente, hasta lograr que todos los
tratamientos hayan sido explícitamente considerados.
Esto se puede esquematizar de distintas maneras (conjuntos, segmentos,
llaves).
Este procedimiento recibe el nombre de refinamiento paso a paso, el lema
didáctico es: “divide y será fácil”.
Teorema de la Estructura
Se basa en el concepto de diagrama o programa
propio, el mismo consiste en que toda estructura
tenga un solo punto de entrada y un solo punto
de salida.
Un diagrama es estructurado si tiene únicamente
como figuras lógicas: secuencia, capacidad de
decisión y capacidad de repetición; y si además
está construido con estructura.
Métodos
Con la filosofía de la programación estructurada distintos autores han desarrollados trabajos
que varían unos de otros en el método, pero todos tienen como bases los conceptos
teóricos de Dijkstra.
Método Jackson. La filosofía del mismo tiene características comunes con la programación
estructurada. Las estructuras básicas se llaman diagramas de bloques y se representan
con los símbolo. La representación de la secuencia de acciones se hace en forma de
árbol, leyéndose de izquierda a derecha a un mismo nivel.
PROGRAMA
INICIO
º
PROCESO
FIN
*
*
SECUENCIAL
ALTERNATIVA
FIN DE ARCHIVO
REPETITIVA
IMPRIME
TOTALES
TOTALES
CALCULO
CARGAS
FAMILIARES
TIENE
º
CALCULO HORAS
EXTRAS
NO TIENE
º
HAY HORAS
º
NO HAY
º
Método Bertini
En esta metodología las estructuras básicas se representan con los siguientes símbolos.
Estas estructuras forman los que se denominan árboles programáticos, donde cada nivel
es, como en otros modelos, los refinamientos que se van realizando.
PROGRAMA
SECUENCIAL
ALTERNATIVA
REPETITIVA
PROGRAMA
PARA CADA
EMPLEADO
FIN
INICIO
HORAS
EXTRAS
CARGA
FAMILIA
NO
SI
NO
SI
Método Warnier
Una de las características de esta manera de hacer programas estructurados consiste
en la representación por medio de lo que se denomina cuadro de descomposición en
secuencias, forma gráfica que utiliza llaves para representar los niveles de
descomposición del problema.
Las estructuras básicas de esta metodología son las siguientes:
• Secuencia: acciones especificadas que no son ni repeticiones ni alternativas. La
secuencia de acciones es de arriba hacia abajo en el cuadro de descomposición de
secuencia
• Repetitiva: En esta estructura, entre paréntesis se escribe el número de veces que
se repite
PRINCIPIO
(1 vez)
PRINCIPIO
(1 vez)
TRATAMIENTO A
(0, 1 vez)
REPETITIVA
TRATAMIENTO
(t veces)
FINAL
(1 vez)
ALTERNATIVA
TRATAMIENTO B
(1, 0 vez)
FINAL
(1 vez)
Comparación con programación tradicional
Veamos un ejemplo práctico …
A partir de los datos ingresados por teclado (Libreta,
Nota1 y Nota2), se desea informar la condición del
alumno (Libre, Regular o Promoción).
Para regularizar y/o promocionar se deberá aprobar los
dos parciales.
Al final informar cuantos alumnos hay en cada una de las
condiciones.
Ventajas
•
Mejor comprensión del problema: se avanza de lo general a lo particular, segmentando en partes
interrelacionadas. Todo programa estructurado puede ser leído desde el principio al fin, sin
interrupciones, en la secuencia normal de lectura. Mejor clarificación del problema.
•
Amortigua la lógica individual: tiende a la construcción lógica normalizada, amortiguando la lógica
individual que en principiantes alcanza altos niveles, y después se arraigan en los programadores
provocando dificultades en la transferencia del mantenimiento de programas.
•
Facilita el trabajo en equipo: Las distintas partes o subprogramas pueden encomendarse a
distintas personas. Un programa puede hacerse entre varias personas.
•
Propende a la formación de la biblioteca propia: Puesto que muchas de estas rutinas pueden
constituir procesos comunes a otras aplicaciones, con lo que se ahorra tiempo de programación.
•
Facilita la prueba: Ya que ésta se realiza sobre partes razonablemente pequeñas, lo que hace mas
fácil identificar los errores. Se realiza un claro seguimiento del problema.
•
Facilita la legibilidad de la documentación: Por ende permite una fácil transferencia de la
aplicación entre distintos programadores, evitando así los dueños de programas, solo lo entienden
los que lo hicieron. El mismo diagrama sirve para documentar.
•
Facilita la optimización, el mantenimiento y las modificaciones: Como está compuesto por
partes razonablemente pequeñas, rápidamente individualizables, es más fácil depurar, mantener o
modificar las mismas. Las modificaciones afectan solamente algunas partes.
Ventajas
Se cometen menos errores: Por la misma naturaleza del método, que divide en partes al problema, y cada
una de esas partes tienen menos instrucciones que el diagrama hecho en forma convencional.
La demostración teórica es la siguiente : e = k * n2 (1)
Donde :
e: cantidad de errores que se cometen en un programa
k: factor de proporcionalidad que depende de la experiencia del programador
n: número de instrucciones del programa
O sea la cantidad de errores es directamente proporcional al cuadrado del número de instrucciones y a la
experiencia del programador.
Supongamos que el programa de n instrucciones lo dividimos en dos subprogramas de n1 y n2 instrucciones
respectivamente, donde n n1 + n2 y en el que la cantidad de errores de cada subprograma es:
e1 = k * n12; e2 = k * n22
Si sumamos:
et = e1 + e2 = k (n12 + n22)
(2)
Si en la fórmula (1) reemplazamos n por su equivalente n1 + n2, se obtiene:
e = k (n1 + n2)2 = k (n12 + n22 + 2 n1 n2) = k (n12 + n22) + k 2 n1 n2
(3)
Si restamos al error del programa e (3), el error de los subprogramas et (2), se tiene:
 = e - et = k 2 n1 n2
Donde  es la cantidad mayor de errores que se cometen en la programación tradicional respecto de la
estructurada.
Esta deducción nos dice que cuando mayor sea la cantidad de subprogramas en que se divide un programa
tradicional, mayor será la diferencia .