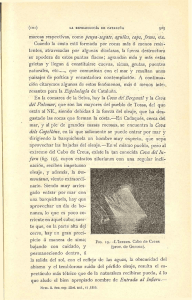
Generador de oleaje aleatorio con motor lineal

ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
ENINVIE – UAZ 2004
Encuentro de Investigación en Ingeniería Eléctrica
Zacatecas, Zac, Marzo 4 —5, 2004
Generador de oleaje aleatorio con motor lineal
Roberto Herrera Charles,
Centro de Investigación y Desarrollo de Tecnología Digital.-IPN
Av. del Parque 1310 Mesa de Otay, Tijuana, B.C. -22510.
TEL: +(664)6231344, ext. 82875, correo-e: [email protected],
Luis P. Sánchez Fernández,
Centro de Investigación en Computación – IPN
Av. Juan de Dios Batiz s/n casi Esq. Miguel Othon de Mendizabal,
IPN Zacatenco 07738. CD. de México.
TEL: +(555)7296000, ext. 56573, correo-e: [email protected],
Resumen — Los generadores de oleaje requieren realizar operaciones cíclicas, que en forma natural
son movimientos lineales, por lo que, estas operaciones son realizada por actuadores o dispositivos con
tales características. Tradicionalmente, estos son implantados por sistemas hidráulicos o cajas de
engranes mecánicos. Este artículo presenta un generador de oleaje con un motor lineal, el cual se
programa para generar diversos oleajes aleatorios, que se utilizan para realizar pruebas
experimentales con modelos físicos a escala en laboratorios de investigación hidráulica.
Abstract — Wavemakers are implemented using hydraulic systems or mechanical transmission.
The progresses of the technology in lineal motor will replace these systems. This paper shows the
wavemaker with a lineal motor. It has been used for experimentals tests of physical scale model in
hydraulic laboratory. The use of lineal motor makes possible the generation of several random sea
waves.
Palabras Clave — motores lineales, generador de oleaje, simulación aleatoria, espectros de oleaje.
I. INTRODUCCIÓN
A
MPLIA parte
de la automatización contiene movimientos lineales de forma natural. Sin embargo,
estos son implantados por motores rotatorios que requieren de mecanismos de transmisión o
bien de accionamientos que utilizan sistemas neumáticos o hidráulicos, como el caso de los
generadores de oleaje que se utilizan en los laboratorios de hidráulica experimental [1] [2]. Estos,
además de aumentar los costos en instalación y mantenimiento, disminuyen la respuesta dinámica y
aumentan la inercia y fricción. Los motores (eléctricos) lineales al no requerir de sistemas mecánicos
de transmisión, transfieren directamente su energía a la aplicación. Sus ventajas [3][4] en relación a
los motores rotacionales son:
• Menor fricción y no existe reacción inversa (“backslash”) lo que resulta en una alta
precisión.
• No poseen limitaciones mecánicas en la aceleración y velocidad; estos son sólo limitados por
el ancho de banda del sistema que mide la posición, usualmente un codificador, y por la
potencia electrónica.
• Alta vida y confiabilidad, debido que no ostentan partes mecánicas y su contacto es nulo o
mínimo.
• Habilidad para ejercer el empuje sobre el elemento móvil sin contacto físico.
1
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
12
Este artículo presenta un sistema basado en un motor eléctrico lineal. Su programación genera
diversos oleajes aleatorios que se utilizan para realizar pruebas hidráulicas experimentales para el
estudio e investigación con modelos físicos a escala.
II. PRINCIPIO TEÓRICO
Los motores lineales aparecieron a finales del siglo XIX. Sin embargo, los últimos 25 años han
marcado su auge y desarrollo. Debido a que sus costos tienden a disminuir, y que los dispositivos y
sistemas modernos requieren de mayor exactitud y velocidad, sus aplicaciones son cada vez más
comunes y frecuentes donde se requiere alta velocidad combinada con precisión.
Fitzgeral et al.[5] exponen que es similar el análisis para los motores lineales y rotacionales. En
general, los desplazamientos lineales equivalen a los angulares, y las fuerzas lineales sustituyen a los
pares de torsión. Bajo estas consideraciones, se pueden usar las mismas deducciones que en los
análisis de motores rotacionales. De hecho, la forma más generalizada de lograr un motor lineal es
desenrollar, de manera imaginaria, un motor de inducción rotatoria, no obstante se desprecia el efecto
punta, que es mínimo a bajas velocidades.
A. Principios teóricos de la operación de los motores lineales
De manera similar a los motores rotatorios, los motores lineales constan de dos partes un rotor y un
estator, que algunos suelen llamar primario y secundario [4][6], aunque no siempre existe esta
correspondencia. El primario generalmente es el que recibe la potencia de la fuente, y también indica
al elemento fijo.
Los principios por los que opera un motor lineal son: 1) Alineamiento magnético. 2) Interacción de
los campos magnéticos y la corriente basado en la ley de Ampere o la ecuación de Lorentz. La
potencia de un motor lineal, de manera análoga a los motores rotatorios está dada por la siguiente
ecuación:
Po = Fv
(1)
Donde Po es la potencia de salida N m/s (Watts); F es la fuerza N ; V es la velocidad en m/s.
Desempeño de los motores lineales. Sea Vs la velocidad síncrona de la onda viajera en un motor
lineal. Si la velocidad del elemento móvil es V, como se muestra en la figura 1, entonces el
desplazamiento S está dado por:
s=
Vs − V
Vs
Secundario
(2)
v
vs
Primario
Figura 1. Motor lineal de inducción
B. La teoría de operación del bucle de servocontrol del motor lineal
El sistema de generador se implanta con el controlador del motor lineal (E100-AT) y con él se
construye un esquema de control (sección 4.a) para la generación de los espectros de energía del
oleaje referidos en la sección 3.b.
El esquema clásico de control, para un motor lineal, es controlar la corriente para determinar la
torsión en función de la velocidad angular y con ello controlar su velocidad. El esquema de control
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
13
para un motor lineal se muestra en la figura 2, que además controla la temperatura y puede controlar
la posición deseada del motor con las curvas almacenadas en la memoria del manejador.
Figura 2. Esquema de servo control para motor lineal Linmot P01-37120
El servo control determina la velocidad deseada con respecto a las secuencias de posiciones. Es
decir, al derivar contra el tiempo las posiciones, se determina la velocidad y posición solicitada, con
el resultante de una corriente; el valor de la corriente determina la fuerza, ésta se aplica al comando
del motor a través de la modulación PWM (Modulación de ancho de pulso).
C. Características del motor lineal utilizado en actuador del canal
Para el sistema de generador de oleaje se utiliza, como actuador, un motor lineal P01-37120/80
160L fabricado por Linmot [7] este es un motor lineal de doble lado (DLIM): Dicho motor tiene
núcleo móvil de 6.3 pulgadas de desplazamiento sobre un montaje para motor lineal PF01-37 100F,
tabla 1. El manejador electrónico E100-AT controla al motor y tiene las características eléctricas:
máxima corriente 3 A, voltaje lógico 4-48 V., voltajes de potencia 48 V. El núcleo móvil del motor
requiere de un lubricante especial para minimizar la fricción y desgaste.
TABLA 1
CARACTERÍSTICA DEL MOTOR LINEAL PF01-37120
Mín. desplazamiento
Máx. desplazamiento
Fuerza Pico
Máxima aceleración
Masa móvil (rotor)
Masa estator
Longitud (rotor)
Radio (rotor)
Longitud (estator)
Radio (estator)
19 µ m
100 mm.
122 N.
247 m/s2
635 g.
740 g.
365 mm.
20 mm.
227 mm.
37 mm.
El controlador del motor lineal (E100-AT) se comanda desde el puerto serie RS-232 de una
computadora personal PC. El motor lineal se posiciona de tres formas: 1) por una curva que se
almacenan en el controlador del motor (ver sección 2.b), 2) por una señal de voltaje analógico y 3)
por el comando de codigo que se envia al puerto RS-232 en linea.
III. PRINCIPIOS DE LA GENERACIÓN DEL OLEAJE
A. Modelo progagación de ondas en un canal de generación de oleaje
La solución a las ondas que se propagan sobre la superficie del agua en un canal son ondas (olas)
que son controladas por la fuerza gravitacional [8]. Cuando un líquido está en reposo posee una
superficie libre horizontal. Cualquier perturbación en la superficie provoca un movimiento en el
líquido, generalmente del tipo oscilatorio, que se propaga sobre toda la extensión de la superficie. Por
lo que, bajo el principio de la hidrodinámica, este movimiento es un movimiento sin vórtices (no
rotacional) y con un potencial de velocidad φ ( x, z , t ) para un campo de velocidad V (u ( x, t )ir, w( z, t )kr) .
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
14
Ecuación de gobierno [9]. La ecuación (3) de continuidad para un flujo de agua se obtiene al
aplicar la ley de conservación de masa o continuidad para un diferencial de volumen o de control.
∂ρ
∂ρ
∂ρ
1 ∂ρ
∂v ∂u ∂w
(
+u
+v
+w )+
+
+
=0
ρ ∂t
∂x
∂y
∂z
∂x ∂y ∂z
(3)
Siendo:
ρ ( x, y, z , t ) es la función de densidad del flujo, v(x,t) su velocidad en x, u(y,t) su velocidad en y, y
w(z,t) su velocidad en z.
El principio de conservación de la masa, establece que no puede aparecer o desaparecer masa en el
interior de un volumen de control, a menos de que esta haya pasado a través de la superficie que
delimita sus fronteras. El término dentro del paréntesis de la ecuación (3) puede verse como la
derivada total de ρ ( x, y, z , t ) con respecto al tiempo:
Dρ dρ
dx
dy
dz
ó
donde u =
v=
w=
Dt
dt
dt
dt
dt
(4)
La ecuación de continuidad (3) de forma reducida queda, tal como se indica en (5).
1 dρ
+ ∇ ⋅V = 0
ρ dt
dρ
para el agua E = 2.07 × 10 9 Nm − 2
E≡ρ
dt
(5)
El agua se considera un fluido incomprensible, debido a que se requiere incrementar la presión a
1x106 N/m2 para obtener un cambio en su densidad de 0.05%. Si consideramos que no cambia su
densidad la ecuación (5) se reduce al Laplaciano del potencial de velocidad.
1 dρ
= 0 ∇ ⋅ V = 0 ó ∇ 2φ = 0
ρ dt
(6)
Esta es la ecuación de gobierno con la que podemos modelar el oleaje en el canal, si consideramos
que se tiene un fluido no rotacional e incompresible.
Dado que solo tenemos propagación de las olas en una sola dirección (x), consideramos un modelo o
ecuación diferencial en dos dimensiones (figura 3), donde las paredes laterales tienen una función de
potencial periódico y la condición frontera del fondo no existe flujo.La parte superficial, que es
nuestro interés, tiene condiciones de frontera cinemáticas y dinámicas dadas por la fuerza de
gravedad.
z
Cinemática de condiciones de
frontera de superficie libre
dφ dη
+
= 0 en z = 0
dz dt
Dinámica de condiciones de
frontera de superficie libre
η=
1 ∂φ
g ∂t
en z = 0
L
H
x
w
u
h
∇ 2φ = ∇ 2ψ = 0
0< x < L
−h < z <η
C. F. L.
φ( x, t ) = φ( x + L, t )
φ( x, t ) = φ( x, t + L )
∂φ
Condiciones de frontera del fondo
w=−
= 0 en z = − h
(Requerimiento cinemática)
∂z
Figura 3. Condiciones de frontera para ondas de frontera libre.
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
15
El potencial de la velocidad en la superficie sigue la forma que toma la ola sobre las coordenadas en
que se desplaza. En el caso del eje z toma una forma hiperbólica, la cual se hace constante su valor
(por ejemplo z = 0) y representar el cambio de nivel del agua en la ecuación (7).
η ( x, t ) =
1 ∂φ
g ∂t
en z = 0
(7)
Otra suposición importante es considerar que el movimiento ondulatorio puede idealizarse, si un
punto de la superficie libre va subiendo y bajando con una aceleración local igual. Esta aceleración
constante g está dada por la fuerza de campo gravitacional el cual es constante si la masa no cambia.
Esto se expresa en
r
r
∂v r
= f = − gk ,
∂t
(8)
∂φ
= − gz + const.
∂t
(9)
De la ecuación de Bernoulli, bajo las consideraciones de las relaciones entre el gradiente y potencial
de una función para un flujo no rotacional, que relaciona la presión con la fuerza de gravedad y la
derivada del potencial de velocidad; y considerando que la presión en la superficie libre es constante
p = 0, se puede obtener la siguiente relación.
c=
g
tanh(kh) .
k
(10)
Resolviendo el sistema de ecuaciones (8) y (9) se tiene la relación de
k = gh ,
(11)
la cual es conocida como la fórmula de Airy. Esta relación expresa la velocidad de desplazamiento
de la onda c en función del número de onda k (“wave number”) y de la profundidad del canal h
conocido como el tirante en el generador de oleaje. Se consideran tres tipos de aproximación para
esta ecuación: Aguas profundas, medias, y someras o pocas profundas. Esta relación está dada entre
la profundidad del canal h y la longitud de la ola L y que influye la interacción entre la profundidad y
la ola.
En aguas profundas tanh(kh) es igual a 1 para valores h/L > 0.5 es decir kh > π y k=c/g. Para
aguas poco profundas tanh(k) es igual a kh para valores de h/L, es decir kh > π /10. Para aguas
intermedias se cumple la formula de Airy. Con estas aproximaciones y la condición dinámica de la
frontera libre, se modela la forma de las olas al propagarse en el canal.
B. Modelo teórico de un generador de oleaje
Considérese un modelo sencillo como el de la figura 4, donde se realiza la medición del oleaje
exactamente enfrente de la paleta o pistón.
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
16
L
z
H
x
h
Paleta o Pistón
que genera el oleaje
S
Figura 4. Esquema de paleta del generador.
Un pregunta interesante es ¿Que relación existe entre el movimiento S de la paleta con respect a la
altura H, el periodo T y la longitud L de la ola producida? Una respuesta simple es la ecuación (12) y
se obtiene al calcular el volumen desplazado por paleta (Sh) que es igual al volumen contenido en la
ola (H/k), si tuvieramos una onda cuadrada de altura H constante, y su número de onda k, en vez de
una senoidal. Es decir, Sh=H/k de la cual tiene la ecuación (12) dado que k = 1/L, en radianes k =
2ð/L ó bien L = 2ð-k.
H/S=h/L
(12)
Este modelo compara el volumen de agua desplazada por la paleta con el agua contenida en la
crestas de las olas.
Un modelo más completo es resolver la ecuación de oleaje dado por las ecuaciones (6) y (10) para
fronteras libres en la superficie, (ver sección 3.a) y con la función de entrada en que una frontera
lateral es la función del generador. La relación que se obtiene es
H 2(cos( 2 k p h − 1)
=
S sinh 2k p + 2k p h
(13)
Donde kp es la constante de número de ola para ondas progresivas y ésta se determina por la
siguiente ecuación
σ 2 = gk p tanh( k p h )
(14)
Siendo; σ la frecuencia σ = 1 / T , g es la constante de gravedad 9.8 m/s2, y h es la altura de nivel
del agua.
La solución supone que la señal que se aplica al pistón es armónica, por lo que el período del
movimiento de la paleta es el mismo que el periodo T del oleaje.
C. Técnicas utilizadas para la generación de series de tiempo del oleaje aleatorio
Se utilizan tres métodos generales, para generar el espectro de potencia del oleaje: El primero,
filtrando una señal de ruido blanco. El segundo, en forma discreta, con una serie de Fourier, dados
los componentes de potencia de cada uno de los armónicos de la serie. El tercero, en la forma
contínua, se dan los parámetros significativos de la altura (H1/3) y período (T1/3) significativo y con
ecuaciones de espectros empíricas como Mitsuyasu [10], Pierson y Moskowitz, JONSWAP[1], etc.,
se puede obtener el espectro continuo a producir. Por ejemplo el espectro de Bretschneider dado por
la ecuación siguiente,
-4
2
(15)
S(f) = 0.257 H 1/3
T1/3 (T1/3 f) -5 e [-1.03(T1/3 f) ] .
A los valores del espectro deseado se multiplica por la función de transferencia, conocida como
ecuación (17) de eficiencia de la paleta que se obtiene al resolver la ecuación diferencial para las
condiciones de frontera libre,
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
F(f, h) =
H
4sinh 2 (kh)
=
⋅
2S 2kh + sinh(kh)
17
(16)
Donde H es la altura de la ola producida en el canal, S es el desplazamiento de la paleta (“stroke”),
y h la profundidad del agua frente a la paleta en el canal. La constante k es el número de ola y está se
determina por la solución de la fórmula de Airy (11) de la teoría de propagación de olas pequeñas.
Ruido blanco: Se produce una señal de ruido blanco, usando un método experimental por ejemplo
el de Gold y Rander [11], esta señal se hace pasar por un filtro digital al cual se le ajustan sus
parámetros para producir el espectro que se desea. Se puede utilizar un filtro que se ajusta de manera
dinámica.
Usando la transformada inversa de Fourier: Se aplica la transformada inversa de Fourier al
espectro de amplitud discreto, obteniéndose la señal de oleaje a producir en el dominio del tiempo.
Con este método se obtiene una fase constante cero para todas las frecuencias. Para el caso en que el
espectro sea contínuo, se divide éste para obtener M bandas de frecuencias características f n con una
ancho frecuencia ( ∆f ), para convertir un espectro discreto y aplicarle el mismo procedimiento, para
obtener el espectro de amplitud a partir del espectro de potencia se aplica la ecuación (17) ó (18)
para el caso discreto y continuo respectivamente.
a n = 2S ( f n )
(17)
a n = 2 S ( f )∆f
(18)
Sumatoria de la serie de Fourier. Este método consiste en obtener la señal η (t) , del espectro a
producir, como una sumatoria de serie de senos (19).
N
η (t) = ∑ sin( n an f t + θ )
n =1
(19)
Donde θ es una variable aleatoria entre [- π , π ]. N es el número de componentes.
El término oleaje aleatorio es usado en este artículo para describir olas, las cuales se generan para
simular un estado de la naturaleza del mar. Aunque en realidad se producen series de tiempo seudo
aleatorias que en determinado período de tiempo se repiten.
IV. SISTEMA DE GENERACIÓN DE OLEAJE
El canal donde se genera el oleaje es una sección rectangular de 12 m. de longitud, 40 cm. de
profundidad y 30 cm. de ancho, construido con una estructura metálica de aluminio y solo en la
parte donde se hacen mediciones experimentales tiene paredes de mica transparente. Inicialmente se
utilizó un motor rotatorio y un sistema de engranes para la generación de oleaje regular (función
seno) que fue sustituido por el motor lineal, figura 6, con el cual se genera oleaje aleatorio (irregular).
El canal está instalado en el Laboratorio de Hidráulica de Ticoman [12] de la Escuela Superior de
Ingeniería y Arquitectura (ESIA-Zacatenco)-IPN.
A. Esquema de control
El esquema de la generación del oleaje aleatorio [13] se muestra en la figura 5. La diferencia de los
espectros indica donde hay que modificar el espectro. Es decir el algoritmo controla con un valor fijo
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
18
para el tipo de espectro a producir y el error modifica al espectro (en sus parámetros). El control ha
de lograr los siguientes objetivos: Eficiencia y precisión como sea posible, operación con oleaje
regular e irregular unidireccional y que no sea influido por las condiciones de las estructuras que se
están estudiando.
M
M’
*R
E
+
Algoritmo de
Control
motor
lineal
C
f
Manejador
del
Motor
f
canal
de oleaje
f
M’= Comando de control
M = Variable a manipular
B = Señal de realimentación
Elemento
de medición
y procesamiento
*R = Referencia
E = Error
C = Canal
B
altura
oleaje
Figura 5. Esquema de control de bucle cerrado.
En el Canal C el proceso a controlar es la producción y propagación del oleaje en el canal. La
ecuación de gobierno está determinada por el Laplaciano del potencial de velocidad (6). El parámetro
de interés, para el modelo de canal, es la velocidad de fase de las olas, que determina el retardo entre
su generación y medición.
Referencia R o valor deseado de la variable a comandar. Para nuestro caso es el espectro del oleaje
aleatorio, que puede ser un oleaje medido en campo o empírico. El espectro se transforma en una
señal por la suma de funciones senos obtenidos por las fórmulas (17) a (19).
Señal de retroalimentación B: Es la altura del oleaje producido. Para determinar su espectro de
energía, esta señal determina las amplitudes de energía que tiene cada una de las componentes del
oleaje producido en el canal.
Señal del Error E: Las amplitudes obtenidas se comparan con los valores de amplitudes del
espectro deseado, el error de cada comparación se utiliza para corregir la amplitud del cada un de las
componentes del espectro producido en el canal.
Salida del algoritmo de control M’: El principio, es enviar la primera señal que se estima con el
modelo y mantenerla operando hasta que se obtienen datos suficientes para estimar el espectro. Una
vez que se tiene un espectro se compara con el calculado. El tiempo de control discreto lo determina:
1) el retardo al propagarse el oleaje producido, y 2) la captura y medición de datos suficientes.
Variable a manipular M: Una vez obtenido los nuevos valores de amplitud del espectro se calculan
su número de onda k, para determinar una nueva señal de comando para general el espectro oleaje
aleatorio.
B. Actuador del generador de oleaje
El motor lineal (figura 6) impulsa la paleta de generador. La paleta es de tipo pistón, el cual es
genera diferentes oleajes. El equipo permite la generación del oleaje continuo en un modo de tiempo
acotado o cíclico. La estimación de espectro se hace con el método parámetrico y se utiliza el
software StudyWave desarrollado en el CIC [12]. Para generar la serie de tiempo se puede utilizar
algoritmos desarrollados en Maple, MatLab o LabVIEW, ya que el manejador sólo requiere generar
una serie de tiempo, que es la curva a almacenar es su memoria y que comandará la posición del
motor lineal.
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
19
Figura 6. Sistema de motor lineal para generación de oleaje aleatorio.
C. Mediciones experimentales
Se realizaron varios experimentos de oleaje aleatorio con el método de ruido blanco. La señal de
ruido es filtrada, con las amplitudes de variación de las funciones de transferencia, que son obtenidas
directamente de la variación del espectro de oleaje y se obtiene una serie de tiempo como se muestra
en la figura 7a. Este método emplea un programa en Labview para obtener la serie de tiempo
aleatoria (figura 7.a) a partir de su espectro de frecuencia (figura 7.b).
.
Figura. 7. a. Serie de tiempo aleatoria
Figura. 7. b Espectro de serie aleatoria.
D. Trabajos futuros
Si se desea describir adecuadamente el oleaje no es suficiente con el espectro del oleaje
unidireccional, por que se puede observar que el registro del oleaje se compone del oleaje
propagándose en múltiples direcciones [1] [14]. Para un modelado más realista es necesario un
espectro de oleaje direccional S ( f ,θ ) . Para producir este tipo de oleaje en laboratorio se utiliza varias
unidades actuadoras (paletas) de generadores por lo que requiere tener un estanque con múltiples
generadores que se pueden coordinar y sincronizar para producir el espectro [15]. Con un manejador
E400-AT se puede manejar y sincronizar hasta cuatro motores, con lo que es factible generar oleaje
aleatorio multidireccional.
V. CONCLUSIONES
La simulación dinámica del oleaje aleatorio puede ser generada a partir pistones que hacen el
desplazamiento armónico de un volumen de agua, la cantidad del volumen depende de la profundidad
del canal del desplazamiento del pistón y la constante de número de ola. Una manera sencilla de
ENINVIE Encuentro de Investigación en IE, 4—5 Marzo, 2004
20
tener un sistema para generar oleaje aleatorio con mayor precisión es un motor lineal controlado por
computadora. Los motores lineales ofrecen amplia ventajas en las aplicaciones que requieren
desplazamientos lineales. Dado que sus condiciones de contacto son mínimas no tiene limitaciones
dinámicas en cuantos a velocidad y aceleración. Este sistema nos permite contar con un equipo
como base experimental para los procesos de oleaje e investigación de algoritmos de generación de
oleaje con técnicas de autoaprendizaje como las redes neuronales.
RECONOCIMIENTOS
Este trabajo de investigación se realizó con los apoyos de COFAA, CITEDI, ESIA y CIC del IPN, México.
REFERENCIAS
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
[14]
[15]
[16]
Y. Goda, Random Seas and Design of Maritime Structures. Scientific World, 2000.
J. L. Carrillo Aguado, “Hidráulica para el desarrollo” Investigación Hoy, IPN sep-oct. 1995.
Lammer, M. G. M., “Linear lead in utrasmooth motion”, Mach, Des., pp 60-64. 1994.
I. Cruz G. y Salvador Dueñas M., Motores Lineales, Tesis ESIME-Zacatenco, México. 1993.
Fitzgeral A.G. et al, Máquinas Eléctricas. Ed. Mac Graw-Hill, México. pp 217-220. 1992.
Sen P. C. Principle of Electric Machines and Power Electronics. Ed. John Wiley, USA. pp. 278-280. 1997.
Sulzer Electronics. Motor User Manual 1.3. Sulzer Electronics. AG. Zurich, 1999. http://www.linmot.com, 1999.
Galvin, C. J. "Wave-Height Prediction for Wave Generators in Shallow Water" Memoria Técnica 4, Marina U.S.A, Coastal
Engineering Research Center, Marzo, 1964.
Dean, R. G. y Dalrymple. Water Wave Mechanisms for Engineers and scientists. World Scientific. USA, 1991.
Mitsuyasu, H.. “On the growth of spectrum of wind-generated waves(2)-spectral shape of wind waves at finite fetch“. Proc. 17th
Japanese Conf. Coastal Engg., 1970, pp 1-7.
Gold B. y Rander Ch. M., Digital Signal Processing. McGraw-Hill 1969.
CIC-ESIA. “Convenio de colaboración Interinstitucional–IPN”, CIC-ESIA-IPN México, octubre de 2002.
Herrera Ch. R. y Sánchez F. Luis Pastor. “Método de Control Automático de Generación de Oleaje Irregular para Laboratorio de
Investigación, Utilizando motores lineales. CICINDI 2002, Pachuca.
Dean, R. G. y Dalrymple. Costal processes. Cambridge, USA, 2002.
Shaffer H. A., Fuchs, J.U. y Hyllested Peter. “An Absorbing Multidirectional Wavemaker for Costal applications”. Proceeding Costal
Engineering, Syndney Australia, 2000.
Barrientos, Antonio et al. Control de Sistemas Continuos. Mac Graw-Hill España. 1996.