Paralelogramos - El cordel de Ariadna

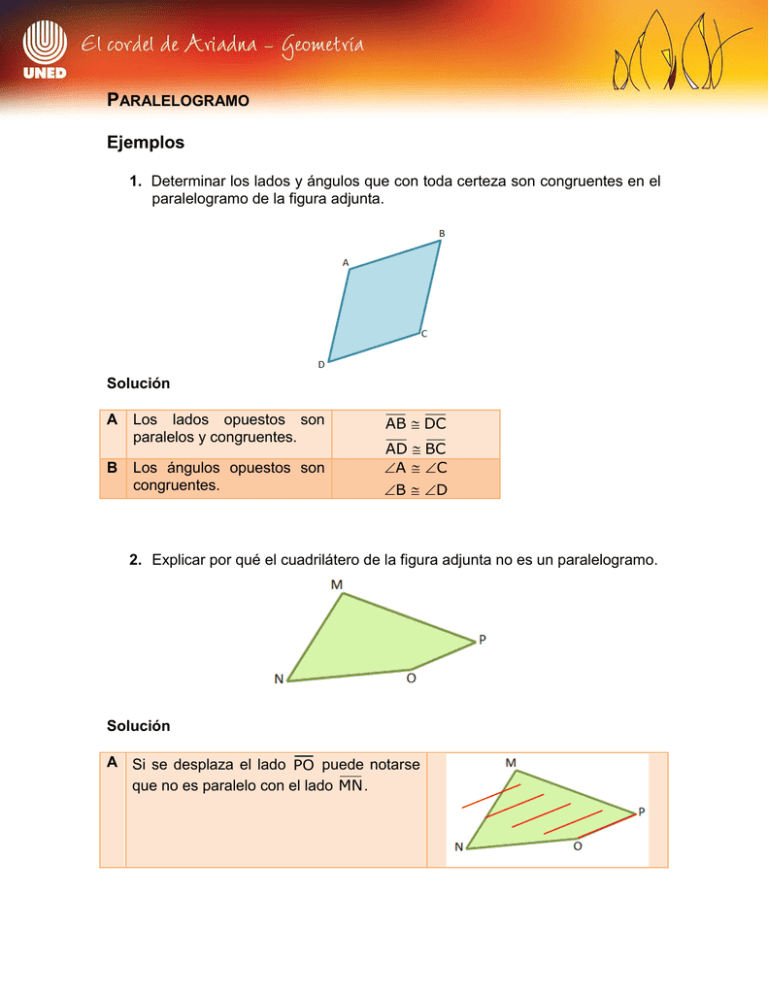
PARALELOGRAMO
Ejemplos
1. Determinar los lados y ángulos que con toda certeza son congruentes en el
paralelogramo de la figura adjunta.
Solución
A
B
Los lados opuestos son
paralelos y congruentes.
Los ángulos opuestos son
congruentes.
AB  DC
AD  BC
A  C
B  D
2. Explicar por qué el cuadrilátero de la figura adjunta no es un paralelogramo.
Solución
A Si se desplaza el lado PO puede notarse
que no es paralelo con el lado MN .
B Si se desplaza el lado NO puede notarse
que no es paralelo con el lado MP .
3. Dibujar un cuadrilátero que tenga un par de lados paralelos pero que no sea
un paralelogramo.
Solución
A
El cuadrilátero tiene dos lados opuestos
paralelos y otros dos lados opuestos que
no son paralelos.
B
Si se desplaza el lado RS puede notarse
que es paralelo con el lado UT .
C
Si se desplaza el lado RU puede notarse
que no es paralelo con el lado ST .
Ejercicios
1. En la figura adjunta se tienen los paralelogramos
calcular la longitud del segmento CE .
ABCD y
DEFG ,
2. Dibuje un paralelogramo y determine los lados y los ángulos que con toda
certeza son congruentes.
3. Explique por qué el cuadrilátero de la figura adjunta no es un paralelogramo.
Soluciones
1.
A En el paralelogramo ABCD sus lados
opuestos son paralelos y congruentes.
B En el paralelogramo DEFG sus lados
opuestos son paralelos y congruentes.
C Se calcula la longitud del segmento CE .
BA  CD
 CD  5 cm
GF  DE
 DE  3 cm
CE  CD  DE
 CE  5 cm  3 cm
 CE  8 cm
2.
A
Se dibuja el paralelogramo.
B
Los lados opuestos
congruentes.
C
son
paralelos
Los ángulos opuestos son congruentes.
3.
A
Si se desplaza el lado EF puede
notarse que no es paralelo con el
lado GH .
B
Si se desplaza el lado FH puede
notarse que no es paralelo con el
lado EG .
y
ST  KH
SK  TH
S  H
K  T