Perpendicularidad y paralelismo

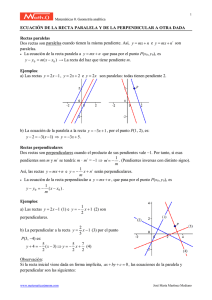
FACULTAD DE CIENCIAS DE LA EDUCACIÓN
CARRERA PEDAGOGÍA EN MATEMÁTICA
Profesor: Rodrigo Jiménez Villarroel
Tema: Perpendicularidad y Paralelismo
1. Se dice que dos rectas son perpendiculares cuando al
cortarse forman cuatro ángulos de igual medida. Por
consecuencia, todos los ángulos iguales son rectos. Se
representa con el símbolo  . En la imagen, se tiene que
MN  PQ .
2. Se dice que dos rectas son oblicuas cuando se cortan y no
son perpendiculares.
3. Postulado: Por un punto exterior a una recta, en un plano,
pasa una y sólo una recta perpendicular a dicha recta.
4. Teorema: Si por un punto exterior a una recta se traza una perpendicular y varias
oblicuas, se cumple:
4.1. El segmento de perpendicular comprendido entre el punto y la recta es menor que
cualquier segmento de oblicua.
4.2. Los segmentos de oblicuas cuyos pies equidistan del pie de la perpendicular son de
igual medida.
4.3. De dos segmentos de oblicuas cuyos pies no equidistan del pie de la perpendicular,
es mayor aquel que dista más.
 Realizar las demostraciones correspondientes.
5. Teorema recíproco del anterior: Si por un punto exterior a una recta se trazan varias
rectas que cortan a la primera, se cumple que:
5.1. El menor de los segmentos comprendidos entre el punto y la recta es perpendicular
a ésta.
5.2. Si dos segmentos oblicuos son iguales, sus pies equidistan del pie de la
perpendicular.
5.3. Si dos segmentos oblicuos son desiguales, el pie del segmento mayor dista más del
pie de la perpendicular que el segmento menor.
 Desarrolle la demostración.
6. La longitud del segmento perpendicular trazado desde el punto a la recta corresponde a
la distancia del punto a la recta.
7. Se dice que dos rectas son paralelas cuando están en
un mismo plano y no se cortan por mucho que se las
prolongue, es decir, no tienen ningún punto común.
 En la figura se tiene que la recta AB es paralela a
CD, es decir, AB CD
8. Teorema: Dos rectas de un plano, perpendiculares a una tercera, son paralelas entre sí.
 Demostración por absurdo.
8.1. Corolario: Por un punto exterior a una recta, pasa una paralela a dicha recta.
Demostrar.
9. Postulado de Euclides: Por un punto exterior a una recta, pasa una sola paralela a
dicha recta.
9.1. Corolario I: Dos rectas paralelas a una tercera, son paralelas entre sí.
9.2. Corolario II: Si una recta corta a otra, corta también a las paralelas a ésta.
9.3. Corolario III: Si una recta es perpendicular a otra, es también perpendicular a toda
paralela a esta otra.
Demostrar.
10. La relación de paralelismo es
10.1. Idéntica, toda recta es paralela a sí misma.
10.2. Recíproca, si una recta es paralela a otra, ésta es paralela a la primera.
10.3. Transitiva, dos rectas paralelas a una tercera, son paralelas entre sí.
11. Paralelas cortadas por una secante
11.1. Postulado: Toda secante forma con dos paralelas ángulos correspondientes
congruentes.
LEMA: Si una secante forma con dos rectas de un plano, ángulos correspondientes
congruentes, dichas rectas son paralelas. La demostración se realiza por el
método de reducción al absurdo.
Demostración lema:
Sea la siguiente construcción auxiliar:
Se trata de demostrar entonces que si 1 y
5 tienen igual medida, entonces las rectas
MN // PQ .
HIP: m1  m5 (puede ser cualquier par
de ángulos correspondientes).
TES: MN // PQ
Supongamos que MN no es paralela a PQ
Entonces se puede trazar una recta paralela a
PQ por el punto O que se llamará TU tal
como lo señala la imagen.
Luego mROT  mPO ' O
Además mMOR  mPO ' O
Entonces mROT  mMOR
Lo que es imposible, a menos que la recta TU coincida con la recta MN . Por lo tanto,
debe cumplirse que MN y PQ sean paralelas.
11.2. Teorema: Toda secante forma con dos paralelas ángulos alternos internos
congruentes. Demostrar y redactar su recíproco.
11.3. Teorema: Toda secante forma con dos paralelas ángulos alternos externos
iguales. Demostrar. ¿Cuál es su recíproco?
11.4. Teorema: Dos ángulos conjugados internos, entre paralelas, son suplementarios.
Demostrar y enunciar su recíproco.
11.5. Teorema: Los ángulos conjugados externos, entre paralelas, son suplementarios.
Demostrar y enunciar su recíproco.
12.
Propiedades de ángulos con lados perpendiculares o paralelos.
12.1. Teorema: Dos ángulos que tienen sus lados respectivamente paralelos y
dirigidos en el mismo sentido tienen igual medida.
12.2. Teorema: Dos ángulos que tienen sus lados respectivamente paralelos y
dirigidos en el sentido contrario tienen igual medida.
12.3. Teorema: Si dos ángulos tienen sus lados respectivamente paralelos, dos de ellos
dirigidos en el mismo sentido y los otros dos en sentido contrario, dichos ángulos
son suplementarios.
12.4. Teorema: Dos ángulos agudos cuyos lados son respectivamente perpendiculares
tienen igual medida.
12.5. Teorema: Dos ángulos, uno obtuso y otro agudo, que tienen sus lados
respectivamente perpendiculares son suplementarios.
12.6. Teorema: Dos ángulos obtusos que tienen sus lados respectivamente
perpendiculares son iguales.
13.
Realizar los siguientes ejercicios:
13.1. A partir de la figura, demostrar que si AB CD entonces 1  2  3  2R
13.2. Demuestre que si CE es bisectriz del BCD
y A  B entonces EC AB
Bibliografía:
L. Galdos. Geometría y Trigonometría. Libro III.
Clemens. Geometría. Capítulo I.
Aguilar, A. Geometría, trigonometría y geometría analítica. Ed. Prentice Hall.