Métodos numéricos para ecuaciones en derivadas parciales

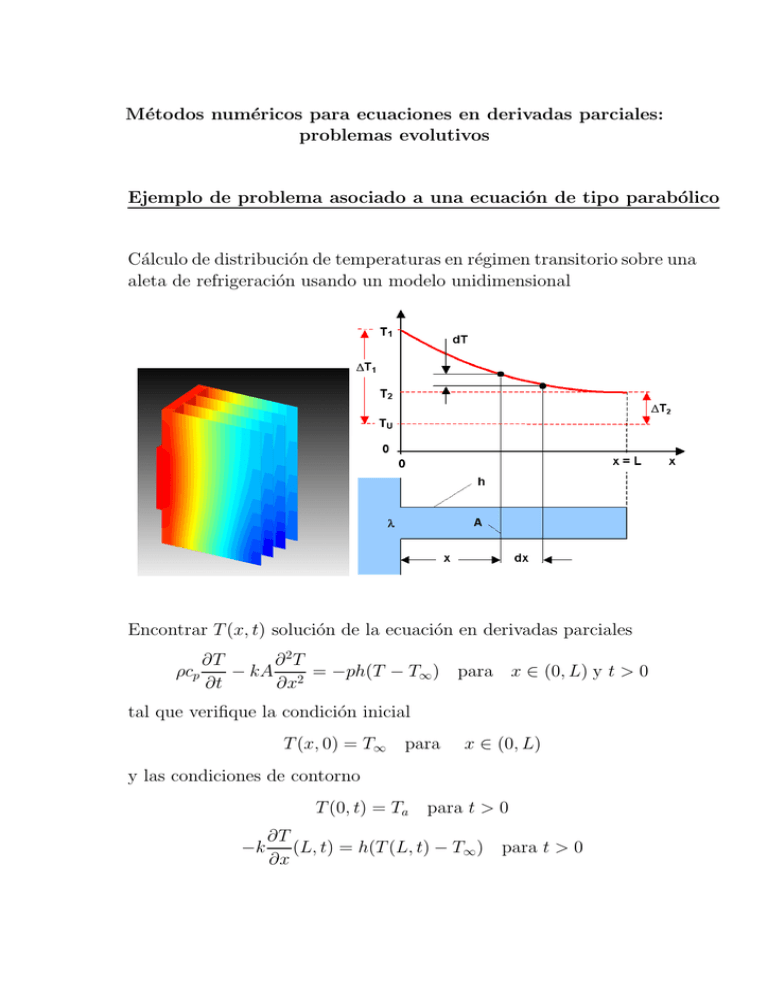
Métodos numéricos para ecuaciones en derivadas parciales:
problemas evolutivos
Ejemplo de problema asociado a una ecuación de tipo parabólico
Cálculo de distribución de temperaturas en régimen transitorio sobre una
aleta de refrigeración usando un modelo unidimensional
Encontrar T (x, t) solución de la ecuación en derivadas parciales
∂ 2T
∂T
− kA 2 = −ph(T − T∞ ) para x ∈ (0, L) y t > 0
ρcp
∂t
∂x
tal que verifique la condición inicial
T (x, 0) = T∞
para
x ∈ (0, L)
y las condiciones de contorno
T (0, t) = Ta
−k
para t > 0
∂T
(L, t) = h(T (L, t) − T∞ ) para t > 0
∂x
Primer paso: semidiscretrización espacial
• Se denota Ti(t) la aproximación de T (xi, t)
• Se usa (de nuevo) la aproximación
∂ 2T
T (xi−1, t) − 2T (xi, t) + T (xi+1, t)
(xi, t) ≃
2
∂x
(∆x)2
para semidiscretizar la ecuación del calor
∂ 2T
∂T
− kA 2 = −ph(T − T∞ )
ρcp
∂t
∂x
en (xi, t) mediante
ρcp
Ti−1(t) − 2Ti(t) + Ti+1(t)
dTi
− kA
= −ph(Ti(t) − T∞)
dt
(∆x)2
• Las condiciones de contorno se tratan como en el problema estacionario:
- en el nodo izquierdo (temperatura conocida)
T1(t) = Ta
- en el nodo derecho (flujo de calor convectivo)
−k
Tnx(t) − Tnx−1(t)
= h(Tnx(t) − Tamb )
∆x
2
Segundo paso: discretización temporal
• Se denota T~ (t) = (T1(t), T2(t), . . . Tnx(t))
• Tras la semidiscretización espacial, se busca el vector T~ (t) solución de
dT~
M
+ K T~ = ~b
dt
para t > 0
con condición inicial
T~ (0) = T~0
• La integración temporal de este problema de valor inicial puede hacerse
con cualquiera de los esquemas estudiados
Algunas observaciones
• La matriz M es diagonal, lo que permite escribir fácilmente el sistema
en la forma
dT~
= K̂ T~ + ~c
dt
tras eliminar T1 (t) y Tnx(t) usando las condiciones de contorno.
• La integración del problema de valor inicial con métodos implı́citos lleva
a resolver un sistema de ecuaciones lineales (dada la linealidad de la
ecuación diferencial) en cada paso
• Debe equilibrarse la tolerancia pedida a ambas discretizaciones (espacial
y temporal)
3
Esquema basado en Euler explı́cito
M
dT~
+ K T~ = ~b
para t > 0
dt
T~ (0) = T~0
• Formulación matricial del método:
T~ n+1 − T~ n
+ K T~ n = ~bn
M
∆t
donde M es diagonal y permite despejar
T~ n+1 = T~ n + ∆t(K̂ T~ n + ~cn )
• Algoritmo de resolución:
- Se toma T~ 0 a partir de la distribución inicial de temperaturas
- Se construyen las matrices M y K
- Para n = 0, 1, 2, · · ·
se calcula T~ n+1 (explı́citamente) a partir de T~ n y ~cn
4
Esquema basado en Euler explı́cito (cont.)
Cálculo de Tin+1 con esquema de Euler explı́cito
• Se discretiza la ecuación
ρcp
dTi
Ti−1(t) − 2Ti(t) + Ti+1(t)
− kA
= −ph(Ti(t) − T∞)
dt
(∆x)2
mediante:
n
n
Tin+1 − Tin
Ti−1
− 2Tin + Ti+1
ρcp
− kA
= −ph(Tin − T∞ )
2
∆t
(∆x)
• Se obtiene ası́ para Tin+1:
Tin+1 = Tin + ∆t
ph n
kA
n
n
n
(T
−
2T
+
T
)
−
∆t
(T − T∞ )
i−1
i
i+1
ρcp (∆x)2
ρcp i
n+1
• Las ecuaciones para T1n+1 y Tnx
se toman de las condiciones de contorno
5
Función aleta mdfevol programada en GNU Octave
Implementación del esquema de Euler explı́cito
• Llamada a función aleta mdfevol:
octave:> [x,T]=aleta mdfevol(L,A,p,k,rho,cp,T0,Tamb,Tini,...
fcnh,nx,tfin,nt);
donde (ayuda con help aleta mdfevol):
L: longitud de la aleta
A: sección (transversal) de la aleta
p: perı́metro (transversal) de la aleta
k: coeficiente de conducción térmica
rho: densidad
cp: calor especı́fico
T0: temperatura en extremo caliente
Tamb: temperatura ambiente
Tini: temperatura inicial
fcnh: función que describe el coeficiente de pelı́cula
nx: número de puntos usados en discretización
tfin: tiempo final de cálculo
nt: número de pasos de tiempo
• Ejemplo: aleta con coeficiente de convección constante
definición de función h(x) (archivo coefh.m)
function h = coefh(x)
h=10;
octave:> L=1;A=1;p=1;k=1;rho=1;cp=1;T0=500;Tamb=300;...
Tini=300;tfin=1;
octave:> [x,T]=aleta mdfevol(L,A,p,k,rho,cp,T0,Tamb,Tini,...
"coefh",10,tfin,1000);
octave:> plot(x,T)
6
Esquema basado en Euler implı́cito
M
dT~
+ K T~ = ~b
para t > 0
dt
T~ (0) = T~0
• Formulación matricial del método:
T~ n+1 − T~ n
+ K T~ n+1 = ~bn+1
M
∆t
donde se debe resolver en cada paso
(M + ∆tK)T~ n+1 = M T~ n + ∆t~bn+1
(la matriz podrı́a factorizarse sólo una vez si ∆t es fijo)
• Algoritmo de resolución:
- Se toma T~ 0 a partir de la distribución inicial de temperaturas
- Se construyen las matrices M y K
- Para n = 0, 1, 2, · · ·
se calcula T~ n+1 resolviendo un sistema de ecuaciones lineales
7
Esquema basado en Euler implı́cito (cont.)
Cálculo de Tin+1 con esquema de Euler implı́cito
• Se discretiza la ecuación
ρcp
dTi
Ti−1(t) − 2Ti(t) + Ti+1(t)
= −ph(Ti(t) − T∞)
− kA
dt
(∆x)2
mediante:
n+1
n+1
Tin+1 − Tin
Ti−1
− 2Tin+1 + Ti+1
ρcp
= −ph(Tin+1 − T∞ )
− kA
2
∆t
(∆x)
• Se obtiene ası́ para Tin+1:
−
kA n+1
ρcp
2kA
kA n+1 ρcp n
n+1
T
+
(
+
+
ph)T
−
T
=
T + phT∞
i−1
i
(∆x)2
∆t (∆x)2
(∆x)2 i+1
∆t i
n+1
• Las ecuaciones para T1n+1 y Tnx
se toman de las condiciones de contorno
8
Función aleta mdfevol2 programada en GNU Octave
Implementación del esquema de Euler implı́cito
• Llamada a función aleta mdfevol2:
octave:> [x,T]=aleta mdfevol2(L,A,p,k,rho,cp,T0,Tamb,Tini,...
fcnh,nx,tfin,nt);
donde (ayuda con help aleta mdfevol2):
L: longitud de la aleta
A: sección (transversal) de la aleta
p: perı́metro (transversal) de la aleta
k: coeficiente de conducción térmica
rho: densidad
cp: calor especı́fico
T0: temperatura en extremo caliente
Tamb: temperatura ambiente
Tini: temperatura inicial
fcnh: función que describe el coeficiente de pelı́cula
nx: número de puntos usados en discretización
tfin: tiempo final de cálculo
nt: número de pasos de tiempo
• Ejemplo: aleta con coeficiente de convección constante
definición de función h(x) (archivo coefh.m)
function h = coefh(x)
h=10;
octave:> L=1;A=1;p=1;k=1;rho=1;cp=1;T0=500;Tamb=300;...
Tini=300;tfin=1;
octave:> [x,T]=aleta mdfevol2(L,A,p,k,rho,cp,T0,Tamb,Tini,...
"coefh",10,tfin,100);
octave:> plot(x,T)
9