Funciones racionales

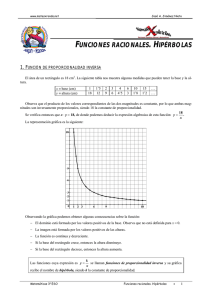
Funciones racionales
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:
.
Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones.
Traslaciones de hipérbolas
Las hipérbolas
son las más sencillas de representar.Sus asítontas son los
ejes. El centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.
A partir de estas hipérbolas se obtienen otras por traslación.
1. Traslación vertical
El centro de la hipérbola es: (0, a).
Si a>0,
se desplaza hacia arriba a unidades.
El centro de la hipérbola es: (0, 3)
Si a<0,
se desplaza hacia abajo a unidades.
El centro de la hipérbola es: (0, -3)
2. Traslación horizontal
El centro de la hipérbola es: (-b, 0). Si b> 0,
unidades.
El centro de la hipérbola es: (-3, 0)
se desplaza a la izquierda b
Si b<0,
se desplaza a la derecha b unidades.
El centro de la hipérbola es: (3, 0)
3. Traslación oblicua
El centro de la hipérbola es: (-b, a)
El centro de la hipérbola es: (3, 4).
Para representar hipérbolas del tipo:
se hace la división entre los polinomios de primer grado que aparecen en la expresión y
se escribe como:
usando la conocida propiedad
Dividendo=Divisor.Cociente + Resto
Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a
los ejes.
El centro de la hipérbola es: (-1, 3).
Funciones definidas a trozos
Son funciones definidas por distintos criterios, según los intervalos que se
consideren.
El dominio lo forman todos los números reales menos el 2.
Función valor absoluto
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los
siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es
negativa se cambia el signo de la función.
4 Representamos la función resultante.
D=
EJERCICIOS:
1Representa las funciones definidas a trozos:
2Representa las funciones valor absoluto:
f(x) = |x - 2|
f(x) = |x² -4x + 3|
f(x) = |x| − x
3Representa las funciones racionales y determina su centro:
f(x) = 6/x
Considera las funciones
a)
b)
c)
4.-
1)
2)
3)
4)
5)
Calcula el dominio de la función b)
Indica en donde se encuentran las asíntotas de la función c)
Calcula los puntos de corte con los ejes de la función a)
Indica cuáles de ellas tienen la gráfica creciente.
Dibuja la gráfica de la función b)
5.A Comenta las características de la gráfica anterior:
Dominio y recorrido.
Signo.
Cortes con los ejes.
Crecimiento y decrecimiento.
Simetrías.
Asíntotas.
Discontinuidades.
B Determina la expresión algebraica de la función f(x) representada anteriormente.
C Obtén gráficamente la solución de las siguientes ecuaciones e inecuaciones.
a. f(x) = 0
b. f(x) = -2
c. f(x) = -10
d. f(x) < 0
D Dibuja en la siguiente representación la gráfica de g(x) = 7x-12 y de h(x) = x2-2x+1.
F Obtén gráficamente la solución de las siguientes ecuaciones e inecuaciones.
a. f(x) = g(x)
b. |f(x)|=|h(x)|
c. f(x) = h(x)
d. f(x)< g(x)
e. h(x) > g(x)