tema: estática i – primera condición de equilibrio

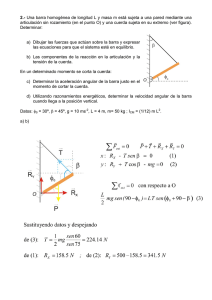
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
SEMANA 01
FÍSICA – Estática I
ESTÁTICA: LA ESTÁTICA ESTUDIA A LAS LEYES Y CONDICIONES QUE DEBEN CUMPLIR LAS
FUERZAS (F) QUE ACTÚAN SOBRE UN CUERPO QUE ESTÁ EN EQUILIBRIO.
1.- Fuerza: Es el resultado de toda interacción manifestada entre dos cuerpos.
1.1.
Medición Estática de la Fuerza: (Ley de Hooke) F = Kx, Hooke, fue el primero
que estableció esta relación mediante el invento de un resorte comprensor para un
reloj. F: fuerza; k: constante;
x: elongación.
1.2.
Naturaleza de las Fuerzas:
*. Fuerza Gravitacional: Es la fuerza de Atracción entre dos cuerpos debido a sus
respectivas masas, estas fuerzas son muy débiles.
**. Peso: El peso de los cuerpos (W) es una fuerza gravitacional y se debe a que la
masa de la tierra (M) atrae a la masa (m) de los cuerpos. W = mg
W: peso; m = masa ; g = aceleración de la gravedad. El peso es un vector que
apunta al centro de la tierra y puede variar de un lugar a otro ya que depende de la
aceleración de la gravedad.
*. FUERZAS ELECTRO MAGNÉTICAS:
*. Fuerza Eléctrica: Es la fuerza de atracción o reacción de dos cuerpos cargados
de electricidad.
*. Fuerzas Magnéticas: Es una fuerza adicional a la eléctrica se da cuando las
cargas están en movimiento.
*. Fuerzas Nucleares: Son fuerzas que se manifiestan cuando las distancias entre
los cuerpos son menores a 10-15m, son fuerzas de corto rango. ( se manifiesta
dentro de los átomos)
2.- Tensión (T) en una Cuerda: Debido a una fuerza(F), jalamos una cuerda fija en un
punto, las moléculas del cuerpo se separan, sin embargo para contrarrestar esta fuerza aparece
una fuerza de restitución llamada Tensión(T), la cual se opone a la fuerza exterior F., dando
origen a una separación imaginaria.
B
M
0
Mg. G. Alfredo Medina Corcuera
0
A
0
F
1
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
M
FÍSICA II
A
T
0
0
CORTE
IMAGINARIO
3.- Comprensión ( C ) en una Barra: Tomemos una apoyada en el punto B y en el otro
extremo A aplicamos una fuerza F que comprime la barra; debido a la fuerza F las moléculas de la
barra se acercan y para contrarrestar este acercamiento aparece una fuerza de resistencia,
llamada comprensión ( C ) la cual se opone a la fuerza exterior.
B
0
M
M
C
A
0
0
F
A
0
0
F
CORTE
IMAGINARIO
4.- fuerza normal:
consideramos un cuerpo pesado sobre una superficie plana; debido al
contacto de las moléculas inferiores se comprimen, producto del contacto aparece una fuerza
llamada normal(n) para contrarrestar el acercamiento molecular, generando una fuerza
perpendicular al contacto.
N
5.- Diagrama de Cuerpo Libre (DCL):
Es el aislamiento imaginario de un cuerpo de
todas las fuerzas externas que actúan sobre el.
*. El Peso (W), verticalmente hacia abajo ( hacia el centro de la tierra)
*. Tensión (T) que siempre sale del DCL, siguiendo la dirección de la cuerda.
*. A lo largo de una misma cuerda de poco peso actúa la misma fuerza de tensión. (T).
*. (N) La Normal aparece del contacto entre dos superficies sólidas.
T
plano inclinado
W
N
DIAGRAMA DE CUERPO LIBRE (D.C.L.).- Es el gráfico de todas las fuerzas actuantes en un
cuerpo en forma aislada.
6.-Ley de Inercia - Primera Ley de Newton:
Si las fuerzas resultantes sobre un
cuerpo es nula, entonces dicho está en reposo o con movimiento rectilíneo uniforme.(MRU).
Mg. G. Alfredo Medina Corcuera
2
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
*. Inercia: Propiedad Inherente a los cuerpos y que les permite conservar su estado de
reposos o de movimiento.
7.-Ley de la Acción y Reacción – tercera ley de Newton.
Si un cuerpo actúa
contra otro con una fuerza llamada acción, el segundo actuará contra el primero con una fuerza de
igual intensidad llamada reacción, esta se dará en la misma recta pero en dirección contraria.
8.- Primera Condición de Equilibrio:
Un cuerpo está en equilibrio de traslación si la
suma de las fuerzas aplicadas sobre el cuerpo es cero. Digamos un cuerpo está en equilibrio
cuando no acelera, esto indica que no debe cambiar de módulo ni la dirección de la velocidad. F
= 0.
El sistema de fuerzas, que actúan sobre el cuerpo en equilibrio de traslación, deben formar un
polígono cerrado.
F1
F2
F3
F1 + F2 +F3 = 0
TEOREMA DE LAMY.-
“Si tres fuerzas coplanares actúan sobre un cuerpo en equilibrio,
éstas necesariamente son concurrentes. El módulo de cada fuerza es directamente proporcional al
seno del ángulo opuesto”.
F3
F1
F
F
= 2 = 3
Senα Senβ Senθ



F2
F1
Mg. G. Alfredo Medina Corcuera
3
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
EJERCICIOS PARA PRACTICAR:
DESARROLLADOS:
1. El sistema mecánico mostrado se encuentra en equilibrio. Sabiendo que:
WA = WC = 20N y WB = 30N, determinar la tensión en la cuerda vertical. No hay
rozamiento.
(1)
(2)
HA
T
RA
WA
(3)
RC
RA
WB
De la figura (1):
RA 
WA
sen
De la figura (3):
Rc 
Wc
sen
De la figura ( 2 ):
F
V
HC
RC
WC
0
T  RA sen  RC sen  WB
T  WA  WC  WB
T  70 N
A)40N
B) 50N
C) 60N
Mg. G. Alfredo Medina Corcuera
D)70N
E) 80N
4
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
2. La figura muestra un rodillo de peso W en equilibrio. Determinar la tensión T en la
cuerda AB. No hay rozamiento. Indique la afirmación correcta.
R
T
W
F
V
F
W  Tsen  R cos 
0
x
0
T cos   Rsen
Combinando ambas ecuaciones:
W  Tsen  T
cos 2 
sen
B) T  W sec
A) T  W cos 
T  Wsen

C) T  Wtg
D) T  Wsen
E) T = W
3. El sistema mecánico mostrado se encuentra en equilibrio. Sabiendo que W = 20N y P =
40N. Hallar el peso del bloque R. No hay rozamiento.
N
P
W
R
F
T
R
A) 20N
0

P W
sen30 0
B) 30N
W  P  .Rsen30 0
R  40 N

C) 40N
Mg. G. Alfredo Medina Corcuera
D) 50N
E) 60N
5
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
4. La figura muestra un sistema mecánico en equilibrio. Sabiendo que W = 20N y P = 50N,
determinar el peso de la polea móvil.
W
w
T1
PP
T1
W
(1)
W
W
P
(2)
(3)
De la figura (1): PP= 2W – T1 = 40N – T1
De la figura (3): T1 = P – W = 30N
En la ecuación anterior:
PP= 40N – 30N = 10N
A) 5N
B) 8N
C) 10N
D) 9N
E) 12N
5.- La figura muestra una esfera de peso W = 50N en equilibrio. Sabiendo que la tensión
en la cuerda oblicua (2) es 150N, determinar el peso del bloque.
T2
T1
Mg. G. Alfredo Medina Corcuera
6
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
W
FÍSICA II
P
De la figura:
W  T2 sen37  P
A) 30N

B) 40N
3
P  150.  50  40 N
5
C) 45N
D) 35N
E) 50N
6.- Calcular el peso P necesario para mantener el equilibrio en el sistema mostrado en la figura.
En el cual A pesa 100 kg, Q pesa 10 kg. El plano y las poleas son lisas. La cuerda AC es
horizontal y la cuerda AB es paralela al plano.
Calcular también la reacción del plano sobre el cuerpo A.
Las fuerzas que actúan sobre el cuerpo A son: el peso 100 kp, la reacción del plano
inclinado N, la fuerza que ejerce la cuerda horizontal que es igual al valor del peso Q=10 kp, la
fuerza que ejerce la cuerda paralela al plano inclinado que es igual al peso P.
Se establece un sistema de referencia cuyos ejes son paralelo al plano inclinado y
perpendicular al mismo, respectivamente. Se sustituye las fuerzas cuyas direcciones no coinciden
con las de los ejes por la acción simultánea de sus componentes rectangulares.
Mg. G. Alfredo Medina Corcuera
7
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
En el equilibrio la resultante de las fuerzas debe ser cero: la fuerza resultante a lo largo del
eje X debe ser cero, y la fuerza resultante a lo largo del eje Y debe ser cero.
Tenemos así, un sistema de dos ecuaciones con dos incógnitas N y P
P=100 sen 30º+10 cos 30º
N+10 sen30º=100 cos30º
El resultado es:
P=58.66 kp
7.- La pluma de 4 m de la grúa de la figura pesa 200 kg y está sosteniendo una carga de 1000 kg.
Calcular: La tensión del cable AB y las componentes de la fuerza que ejerce la articulación C
Una articulación ejerce una fuerza cuyo módulo es desconocido y cuya dirección también lo es.
De forma equivalente, podemos decir que las componentes rectangulares Fx y Fy de dicha fuerza
son desconocidas.
Podemos ponerlas en principio con cualquier orientación, Fx hacia la izquierda o hacia la derecha,
Fy hacia arriba o hacia abajo. Ahora bien, la disposición de las demás fuerzas nos sugiere en la
mayor parte de los casos, el sentido correcto de dichas componentes.
La resultante de las fuerzas es cero
Mg. G. Alfredo Medina Corcuera
8
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
Fy=T sen30º+200+1000
Fx=T cos 30º
La suma de los momentos respecto de la articulación es cero
-200 (2cos60º-1000) 4cos60º + T(4sen30º) = 0
De la última ecuación obtenemos T=1100 kp
8.- En el problema esquematizado en la figura, la barra tiene una longitud de 5 m y pesa 20 kg, el
cilindro tiene un peso de 30 kg y un radio de 0.5 m. Suponer que no hay rozamiento entre la barra
y el cilindro, y que el coeficiente est tico de rozamiento entre el extremo derecho de la barra y el
plano horizontal es 0.3. La esfera está sujeta, a su vez, por una cuerda de 1.3 m de longitud.

Calcular la fuerza de rozamiento y la tensión de la cuerda cuando el ángulo entre la barra y
el plano horizontal es de 15º.
¿Deslizará o no la barra?, razonar la respuesta.
I En este problema hemos de tener en cuenta que la fuerza de rozamiento que actúa sobre un cuerpo
apoyado en un plano es en general, una magnitud desconocida. Solamente podemos expresarla
mediante una fórmula cuando el cuerpo está a punto de deslizar o está deslizando.
Cuando el cuerpo está a punto de deslizar, la fuerza de rozamiento tiene el valor máximo Fr=eN,
donde N es la reacción del plano a lo largo del que desliza el cuerpo, y e es el coeficiente estático
de rozamiento.
Equilibrio de la barra
Mg. G. Alfredo Medina Corcuera
9
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
La resultante de las fuerzas es cero
F cos15º+N=20
F sen15º=Fr
La suma de los momentos respecto al extremo derecho de la barra es cero
N(0)+Fr(0) - Fx+20(2.5)cos15 =0
El valor de x (brazo de F) y el ángulo q se obtienen de la figura

De la ecuación de los momentos obtenemos el valor de F, fuerza que ejerce el cilindro sobre la
barra F=12.7 kp.
Y de las dos primeras ecuaciones despejamos Fr=3.3 kp y N=7.7 kp.
Equilibrio del cilindro
Mg. G. Alfredo Medina Corcuera
10
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
Todas las fuerzas que actúan sobre el cilindro pasan por su centro. La resultante es cero.
N'=T sen+F cos15º+30
F sen15º=T cos
Se obtiene:
T=3.6 kp y N'=43.6 kp
El máximo valor de la fuerza de rozamiento es 0.3 N=2.31 kp. El valor calculado es Fr=3.3 kp.
Luego la barra NO puede estar en equilibrio en esta posición.
CA I
AUTO-EVALUACIÓN
1. Una barra ingrávida se encuentra en equilibrio. hallar la deformación que experimenta el
resorte de K = 30 N/cm, debido al peso del cuerpo de 300N.
a) 5 cm.
b) 10cm. c) 20cm. d) 25 cm.
e) 30cm.
K
30º
2. Una esfera homogénea de 40 kg se mantiene en equilibrio. Determine la deformación del
resorte ideal de K = 250 N/cm. (g= 10m/s2, superficie lisa).
a) 2cm
b) 3cm
c) 4cm d) 5cm
e) 6cm
37º
Mg. G. Alfredo Medina Corcuera
11
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
3. Una barra homogénea de 16Kg se encuentra en reposo tal como se muestra. Si el módulo de
la reacción en "A" es de 100N. Determine el módulo de la reacción "B" (g=10m/s2)
a) 80N
b) 160N
c) 180N d) 100N e) 120N
A
37º
B
4. Si el bloque de 2Kg está en equilibrio bajo la acción de la cuerda AB y de la fuerza
determinar la fuerza de tensión en la cuerda AB. (g = 10m/s2)
a) 4 ˆi + 5 ˆj b) –4 ˆi + 5 ˆk c) -5 ˆi + 10 ˆj -20 ˆk d) -5 ˆi - 10 ˆj +20 ˆk
e) 5 ˆi +10 ˆj +20 ˆk
F  10j  5i
,
z
A
g
y
B
F
x
5.- En el sistema mecánico mostrado el bloque de 8kg se encuentra en equilibrio bajo la acción de
la fuerza F=50N y de las cuerdas AB y BC, que lo sostienen. Si la fuerza de tensión en la
cuerda AB es (-50 ˆi +60 ˆj -30 ˆk ) N, determinar la fuerza de tensión en la cuerda BC. (g = 10m/s2)
a) 10 ˆi - 20 ˆj +20 ˆk
b) -15 ˆi -20 ˆj +30 ˆk c) 50 ˆi +20 ˆj -20 ˆk d) 50 ˆi -20 ˆj e) 20 ˆi -30 ˆk
y
C
A
B
x
F
z
6. Determinar el momento de la fuerza F = 50N, paralela al eje "Y", respecto al origen de
coordenadas.
a) 100 ˆk - 150 ˆi b) -200 ˆk +150 ˆi c) 200 ˆk -150 ˆi
d) 200 ˆi -150 ˆk
e) 200 ˆj +150 ˆi
Mg. G. Alfredo Medina Corcuera
12
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
z
F o
y
3m
1m
3m
x
7.- Se muestra el D.C.L. de un tronco que realiza un M.R.U. Determine la masa de dicho tronco
(g=10m/s2)
a) 10kg
b) 12kg
c) 18kg d) 128kg e) 12,8kg
mg
V
30º
128N
128N
8.- Una barra OA de 30 kg de peso y 2 m de longitud, articulada en O, se apoya sobre una caja
rectangular de 10 kg de peso y de dimensiones 0.75 y 0.5 m. La caja puede deslizar sobre el
plano horizontal. Sabiendo que el ángulo entre la barra y el plano horizontal es de 30º, calcular:


La fuerza sobre la articulación O
La fuerza que ejerce plano horizontal sobre la caja y su punto de aplicación.
 ¿Deslizará o no la caja?. Razona la respuesta.
Dato: el coeficiente estático de rozamiento entre la caja y el plano horizontal vale 0.5
Mg. G. Alfredo Medina Corcuera
13
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
9.- Calcular el peso máximo del disco de la figura, sabiendo que la tensión máxima que puede
soportar la cuerda es de 15 kg.

Calcular también la reacción en la articulación A
Datos: peso de la barra 6 kg, longitud 40 cm; radio del disco 20 cm.
10.- Se levanta un cuerpo de 200 kgf mediante un plano inclinado de 2,8 m de largo y 1,5 m de
altura. El extremo de la cuerda que sube el cuerpo, se adapta a un torno, cuya manivela es de 0,8
m y el radio del torno es de 0,2 m. ¿Cuál es la potencia aplicada al torno, para mantener el
sistema en equilibrio?
Respuesta: 26,75 kgf
11.- En un taller mecánico, se levanta el motor de un automóvil, cuyo peso es de 350 kgf, por
medio de un aparejo diferencial. Si los radios de las poleas son R = 15 cm y r = 12 cm, ¿cuál es la
fuerza que equilibra ese peso?
Respuesta: 35 kgf
12.- Los radios de un aparejo diferencial son R = 20 cm y r = 15 cm. Si se aplica una fuerza de 80
kgf, ¿cuál es el peso del cuerpo que la equilibra?
Respuesta: 640 kgf
13.- Calcular a que distancia de una potencia de 60 kgf estará apoyada una barra rígida de
hierro, para equilibrar un cajón de 300 kgf que está a 0,75 m del apoyo.
Respuesta: 3,75 m
14.- Calcular la potencia que es necesario aplicar a una polea fija, para levantar un peso de 80
kgf.
Respuesta: 80 kgf
15.- Sobre un cilindro de 30 cm de diámetro (que puede girar en torno a un eje), está arrollada
una soga. Si se le aplica una fuerza de 1,8 kgf, ¿cuál es el valor del momento que hace girar el
cilindro?
Respuesta: 0,27 kgf
Mg. G. Alfredo Medina Corcuera
14
UNIVERSIDAD CATÓLICA “LOS ANGELES” DE CHIMBOTE
FÍSICA II
SABÍAS QUÉ...
ALBERT EINSTEIN (1879 – 1955)
La obra del matemático y físico alemán Albert Einstein le ha convertido en uno de los científicos
más famosos de la historia. Sus teorías acerca de la relatividad introdujeron un nuevo y revolucionario
modo de pensar en el espacio, el tiempo y el Universo. También estableció la relación entre masa y
energía con la famosa ecuación E=mc2.
Einstein adquirió la ciudadanía estadounidense en 1940. Se opuso a la guerra a pesar de que,
paradójicamente, sus teorías fueron utilizadas para fabricar bombas nucleares, las armas más
destructivas que han existido jamás. Einstein vio muchas de sus teorías confirmadas
experimentalmente mientras vivió.
Mg. G. Alfredo Medina Corcuera
15