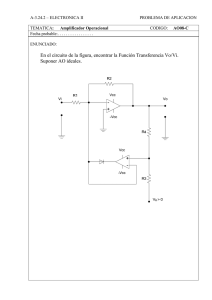
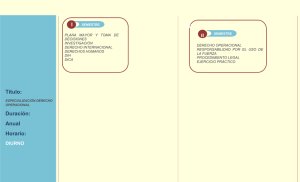
ω ω π ω ω

Electrónica Analógica (305-010-303)
Diciembre 2009
SOLUCIONES
APELLIDOS Y NOMBRE:
DNI:
------------------------------------------------------------------------------------------------------------------------1) Se desea realizar un oscilador senoidal empleando la red pasiva mostrada en la figura, cuya
función de transferencia se indica. Se pide:
R
C
V1
10C
R= 10 k
C= 22 nF
V2
=
V1
V2
10R
10
1 

21 + j 100ωRC −

ωRC 

a) Dibujar el esquema de un oscilador senoidal que utilice:
La red pasiva indicada
Un amplificador operacional ideal
El menor número posible de componentes adicionales (resistencias, etc.).
Se debe justificar el valor de los componentes adicionales.
(2 puntos)
SOLUCION:
La red RC presenta una transferencia real cuando se
anula la parte imaginaria del denominador. En estas
condiciones:
V2 10
=
V1 21
Para obtener la condición de oscilación (GB=1), se
debe utilizar un amplificador no inversor con
ganancia 21/10 = 2,1
La ganancia del amplificador es 1+R2/R1, por lo que:
1+R2/R1 = 2,1
R2= 1,1 R1
(R2 debería ser algo mayor que 1,1 R1 para garantizar el arranque)
b) Determinar la frecuencia de oscilación. (1 punto)
SOLUCION:
Para que exista oscilación, la red RC debe presentar una transferencia real:
ω 2 R 2C 2 =
1
100
ω=
1
10 RC
f =
1
= 72,3Hz
20πRC
2) El amplificador operacional del circuito de la figura se
puede considerar ideal, excepto por tener la tensión de salida
limitada a los valores de alimentación. El comportamiento de
los diodos queda definido por las siguientes expresiones:
V D < 0,7 V → ID = 0
ID > 0 → V D = 0,7 V
a) Determinar las tensiones Va, Vb y Vc en función de Ve,
para valores de Ve en el intervalo –1V < Ve < 1 V.
Representarlas con las acotaciones oportunas. (2,5 puntos)
SOLUCION:
Este circuito es un rectificador de media onda con dos
salidas (Va y Vc).
Se supone que el operacional no se satura.
Va
El estudio se realiza para dos situaciones diferentes: Ve<0 y
Ve>0.
Ve
1
Ve
-1
Si Ve<0:
-2
D1 OFF → Va= 0
D2 ON → Vc = −
1
R3
⋅Ve = −2 ⋅Ve
R1
Vb = Vc + 0,7 = 0,7 − 2 ⋅Ve
Vb
2,7
Vbmin= 0,7V ; Vbmax= 2,7V
Los valores máximo y mínimo de Vb no alcanzan la
saturación.
0,7
-1
-0,7
-2,7
Si Ve>0:
Vc
R
D1 ON → Va = − 2 ⋅Ve = −2 ⋅Ve
R1
2
1
D2 OFF → Vc= 0
Vb = Va − 0,7 = −0,7 − 2 ⋅Ve
Vbmin= -2,7V ; Vbmax= -0,7V
-1
Los valores máximo y mínimo de Vb no alcanzan la
saturación.
b) Indicar de forma razonada cuál es la función que realiza este circuito y para que margen de
tensiones de entrada funciona correctamente. (1 punto)
SOLUCION:
Es un rectificador de media onda con 2 salidas: En Va se obtienen las semiondas negativas
(con Ve>0). En Vc se obtienen las positivas (con Ve<0).
Funciona correctamente mientras el operacional no se satura. Vesatpos= (0,7-10)/2= -4,65V.
Vesatneg= (-0,7+10)/2= 4,65V. Funciona bien para -4,65 < Ve < 4,65 V.
Ve
3) El cicuito de la figura utiliza un operacional que
se puede considerar ideal excepto por tener limitada
la tensión de salida al margen definido por las
tensiones de alimentación (± Vcc= ± 10 V). En el
instante t=0 el condensador está descargado.
R1= 50 k
R2= 200k
C1= 100nF
R3= 3,3 k
R4= 2,2 k
a) Obtener una expresión analítica de Vo en función
de V1 y V2 en el dominio del tiempo, que sea
válida para t >= 0 (en este apartado suponer que el
operacional no está saturado). (2 puntos)
SOLUCION:
El circuito es un integrador inversor con dos entradas. Tiene la peculiaridad de que la
entrada no inversora (V + ) del operacional está conectada a una tensión constante, pero
distinta de cero.
Calculamos el valor de V +
V + = Vcc ⋅
R4
2.2
= 10 ⋅
= 4V
R3 + R4
3.2 + 2.2
Ahora calculamos las corrientes i 1 e i 2 que fluyen por las resistencias R1 y R2. Por
comodidad, las consideramos positivas si fluyen de derecha a izquierda.
i1 =
V + − v1 4 − v1
=
R1
50k
V + − v2 4 − v2
i2 =
=
R2
200 k
La corriente que fluye por el condensador C 1 (en sentido de derecha a izquierda) es:
ic = i1 + i2 =
4 − v1 4 − v2
+
50k
200k
Expresando la corriente i c en amperios y las tensiones en voltios:
ic = 10 −6 ⋅ (100 − 20 ⋅ v1 − 5 ⋅ v2 )
La tensión v o en el instante t=0, y puesto que el condensador está inicialmente descargado,
es:
vo (t = 0) = V − = V + = 4V
Para t>0, el condensador se carga debido a la corriente i c . Como la tensión en su borna
izquierda es constante e igual a 4V, será la tensión v o (t) la que cambie de valor con el
tiempo. Por lo tanto:
vo =
1
10 −6
i
dt
=
(100 − 20 ⋅ v1 − 5 ⋅ v2 )dt = 10 ⋅ ∫ (100 − 20 ⋅ v1 − 5 ⋅ v2 )dt
c
C1 ∫
C1 ∫
teniendo en cuenta que el condensador tiene una capacidad de 100 nF = 10 -7 F.
Finalmente, la expresión analítica pedida en este apartado se obtiene sacando el término
constante (1000·t) fuera de la integral, e imponiendo la condición inicial v o (t=0)= 4V.
vo = 4 + 1000 ⋅ t − 10 ⋅ ∫ (20 ⋅ v1 + 5 ⋅ v2 )dt
(t en segundos; v o , v 1 y v 2 en voltios)
b) Determinar y representar gráficamente con las acotaciones oportunas la evolución temporal de
la señal en Vo (en el margen 0 a 6 milisegundos) , cuando se aplica la señal V1 indicada, siendo
V2= 0 . (1,5 puntos)
SOLUCION:
Se estudia en primer lugar el tramo 0 < t < 3 ms, durante el que v 1 = v 2 =0.
V1 (V)
vo = 4 + 1000 ⋅ t
Para t= 0, v o = 4
6
Para t= 3 ms, v o = 4+3 = 7V
t (ms)
0
Para estudiar el segundo tramo (3 < t < 6 ms) se
parte del final del primer tramo (v o = 7V).
Tomando como nuevo origen de tiempos el
comienzo de este tramo, y sabiendo que v 2 =0 ,
vo = 7 + 1000 ⋅ t − 200 ⋅ ∫ v1dt
Vo (V)
7V
6,4V
4V
Para t=0 (3 ms tiempo absoluto)
t (ms)
vo ( t = 0 ) = 7
y para t=3ms (6 ms tiempo absoluto), con v1= 6V
vo (t = 3ms ) = 7 + 1000 ⋅ t − 1200 ⋅ t = 7 − 200 ⋅ t
vo (t = 3ms ) = 7 − 200 ⋅ 3m = 7 − 0,6 = 6,4V
Gráfica obtenida mediante simulación.
0
3
6