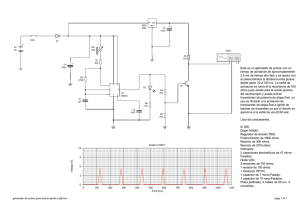
45 F Ejercicios Complementarios

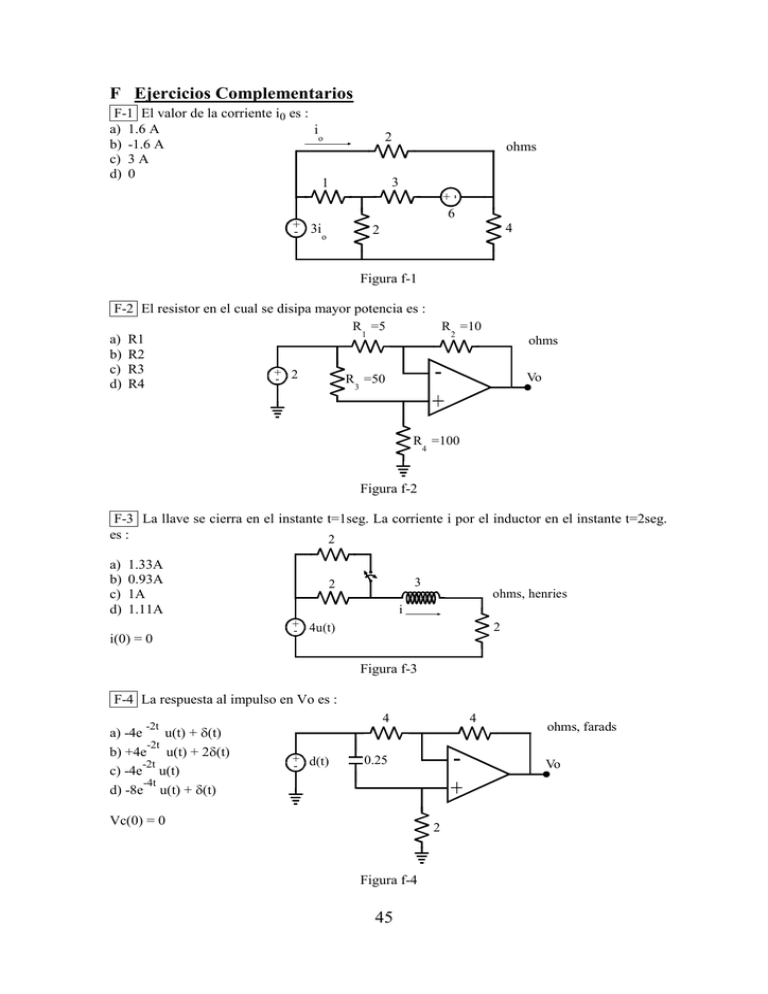
F Ejercicios Complementarios
F-1 El valor de la corriente i0 es :
a) 1.6 A
i
o
b) -1.6 A
c) 3 A
d) 0
1
2
ohms
+
-
3
6
+ 3i
o
4
2
Figura f-1
F-2 El resistor en el cual se disipa mayor potencia es :
R =5
1
a) R1
b) R2
c) R3
+ 2
R =50
d) R4
3
R =10
2
ohms
Vo
R =100
4
Figura f-2
F-3 La llave se cierra en el instante t=1seg. La corriente i por el inductor en el instante t=2seg.
es :
2
a)
b)
c)
d)
1.33A
0.93A
1A
1.11A
i(0) = 0
3
2
ohms, henries
i
+ 4u(t)
-
2
Figura f-3
F-4 La respuesta al impulso en Vo es :
4
-2t
a) -4e
u(t) + δ(t)
-2t
b) +4e u(t) + 2δ(t)
-2t
c) -4e u(t)
-4t
d) -8e u(t) + δ(t)
+ d(t)
-
4
0.25
Vc(0) = 0
Vo
2
Figura f-4
45
ohms, farads
F-5 Encontrar la expresión analítica de la respuesta al escalón de la red, Vo (t). Dibujar la
respuesta en función del tiempo, en escala.
1mhy
Vo(0) = 0
i(0) = 0
+
i
+ u(t)
-
1 nf
1K
Vo(t)
-
Figura f-5
F- 6 El valor de la resistencia equivalente de Thevenin vista entre los terminales a-a` es :
2
a)
b)
c)
d)
3.5 ohms
2.7 ohms
1.5 ohms
2 ohms
2
a
ohms
+
V
2V
1
1
1
-
a´
Figura f-6
F- 7 El valor de R1 es tal que V2 = -10v. La potencia disipada en R1 es :
1K
1K
1K
ohms
a) 1/8 w
b) 8 mw
R
c) 64 mw
1
1 +d) 1w
V
2
Figura f-7
F- 8 La llave cambia de posición en t=1seg. La tensión V en el instante t=1.2seg es :
3
a)
b)
c)
d)
5v
4v
1.63v
3.26v
ohms, farads
+
+ 8 u(t)
-
0.2
3
0.2
V
-
V(0) =0
Figura f-8
46
i
+
-
F - 9 En la red de la figura, el interruptor se cierra y se alcanza el estado permanente en ella. En
t=0 el interruptor se abre. La expresión de i (t) es : ( todos en mA )
-t/90ns
7
a) -20.5 e
cos ( 10 t +_/8 )
100
ohms, henries,farads
b) (-0.8+15t) e-107t
c)
7
-107t
V
1.7 e
cos (10 t + 10 _ )
d)
-t/10ns
-t/1us
-0.25 e
+ 25.25 e
1µH
5 +10nF
100
Figura f-9
F - 10 Obtener y graficar las respuestas Vo (t) al escalón y al impulso.
10K
Vo(t)
Vs +-
18 nF
15K
15K
Figura f-10
F - 11 La tensión de Thevenin entre 1-1` es :
a)
b)
c)
d)
i
0
1v
5v
12v
2
4
1 ohms
4
5 +-
+ 3i
-
1´
Figura f-11
F - 12 La inductancia equivalente del circuito de la figura es :
L =L2 = 1H
1
a) 0
b) 1Hy
c) 2Hy3Hy
L
M=0.5H
1
M
L
2
Figura f-12
47
F - 13 El instante de tiempo en el cual la tensión sobre el capacitor es 0 volt es :
a) 2.7 seg.
b) 6.9 seg.
c) 10 seg.
d) J
Vc(o) = 0
10
ohms, farads
Vc
+
10u(t)
2
u(t)
10
Figura f-13
F - 14 La respuesta Vo (t) al impulso es :
a)
b)
c)
d)
u (t)
d (t) + u (t)
(1 + t) u (t)
-t
e u (t)
1
d(t)
ohms, henries
+
Vo(t)
1
Figura f-14
F - 15 Hallar el valor de R1 para que la respuesta al escalón Vo (t) sea críticamente
amortiguada.
C
R
1
R
2
Vo(t)
Vs +-
C
Figura f-15
F - 16 El valor de la corriente i es :
a)
b)
c)
d)
0
0.93 A
1.57 A
3.21 A
+ Va 2
+
4 -
2
ohms
i
4
3Va
Figura f-16
F - 17 El equivalente de Norton entre los terminales a-a` es :
a) 2A senwt // 5 ohms
b) 4A senwt // 8 ohms
c) -1A senwt // 8 ohms
d) -1 A senwt // 2 ohms
Is = 2 sen wt
a
i
s
10
10
a´
1:2
(ideal)
Figura f-17
48
ohms
F - 18 La llave cambia de posición en el instante t=1seg. La corriente i por el resistor en el
instante t=2seg. es :
2
ohms, henries
a) 0.383 A
b) 0.766 A
c) 1.73 A
2
+ 4u(t)
2
d) 2 A
Figura f-18
F - 19 La respuesta al impulso en Vo es :
-t/25.2
a) -δ(t) + e
u(t)
-t/25.2
b) 2 δ(t) + 25.2 e
u(t)
-t/25.2
c) δ(t) - e
u(t)
-t/25.2
d) [ 2 + ( 1 - e
) ] u(t)
220nF
ohms, farads
180K
180K
180K
180K
Vo
d(t) +-
Figura f-19
F - 20 Encontrar la expresión analítica de la respuesta al escalón de la red, Vc (t). Dibujar la
respuesta en función del tiempo, en escala.
1mH
1K
ohms, henries, farads
Vc(0) = 2V
i
i(0) = 0
+
u(t)
Vc 1nF
1K
Figura f-20
F - 21 El equivalente Thevenin entre los terminales a-a` es :
a)
b)
c)
d)
-111mV // 5450 ohms
110mV // 10K
-111mV // 475 ohms
356mV // 927 ohms
10K
1K
0.01 +-
1K
+
V
1
-
Figura f-21
49
a ohms
V1
25
10K
a´
-3
-2
F - 22 En el instante t=10 seg. se abre la llave. La tensión Vo en el instante t=10 seg. es :
a)
b)
c)
d)
100
3.76V
7.53V
11.3V
0
0.1 u(t)
10K
i
10µF
+
Vo
-
1K
ohms, farads
10i
10u(t)
Figura f-22
F - 23 La respuesta al impulso Vo (t) del circuito es :
a)
b)
c)
d)
-2t/RC
-2/RC e
u(t)
-2t/RC
-2/RC e
u(t) - 2 δ(t)
-2 δ(t)
-2 d(t) - RC δ´(t)
R
R
R
C
d(t) +-
Vo
Figura f-23
F - 24 En la red de la figura se ha alcanzado en t=0 el estado permanente. En t=0 el interruptor
se cierra. La expresión de Vc(t) es :
a) ( 1+ 17.2 t ) mV e -33 10 6 t
7
c) 25.2 mV e -1.1 10 6 t cos ( 9.9 10 t + 45 °)
b) -0.25 mV e -9.9 10 7 t + 25.2 mV e -1.1 10 6 t
6
d) 8.8 mV cos ( 1.1 10 t + 45 ¬°°°) e -9.9 10 7 t
10nH
0.01
5
ohms, henries, farads
0.01 +
Vo(t)
1µF
Figura f-24
F - 25 El equivalente Thevenin visto entre 1 y 1´ es : [ Vth/Rth ]
a)
b)
c)
d)
100 V / 0.45 ohms
0.5 V / 100 ohms
0.314 V / 37.3 ohms
0.0083 V / 98.3 ohms
10K
i
1 ohms
1K
u(t) +-
10K
100i
100
1K
1´
Figura f-25
50
F - 26 Entre 1 y 1¨ del circuito del problema anterior se conecta la siguiente red . El valor de
-6
V0(t) para t= 6.28 10 seg. es :
ohms, farads
a) 0
1mH
b) 0.314 V
i
c) 0.52 V
d) -0.157 V
1nF
Vc(0) = 0
i(0) = 0
Figura f-26
F - 27 Obtener y dibujar las respuesta al escalón y al impulso del circuito de la figura.
C
R
R
R
R = 100K
C = 1µF
Vc(0) = 0
Vo
R
Vs
+
-
R
Figura f-27
F - 28 En el circuito de la figura la corriente de Norton entre los terminales 1 y 1´ es :
a)
b)
c)
d)
100K
0.95 mA
4.07 mA
10.7 mA
0.1 A
1K
1
0.04V
+
V1
-
1
ohms
10K
10K
100
+ 1
-
1´
Figura f-28
F - 29 En el circuito de la figura la resistencia de Thevenin entre los terminales del capacitor
es:
a)
b)
c)
d)
R
R/2
R/4
2R
51
En el mismo circuito la respuesta al impulso es :
-t/T
a) -Vs/2T e
u(t)
-t/T
b) -Vs/T e
u(t) + 2 Vs δ(t)
R
-t/T
c) Vs/T e
u(t) - Vs δ(t)
-t/T
+ u(t)
d) -Vs/2T e
u(t) + Vs δ(t)
R
ohms, farads
R
R
Vo
R
C
R
Figura f-29
F - 30 En el circuito de la figura la máxima tensión sobre el capacitor es :
a)
b)
c)
d)
1V
2V
32.6 V
74.5 V
1mH
+ u(t)
-
La llave se encuentra cerrada
Se abre en t = 1mseg.
ohms, henries, farads
+
10K
1µF
Vo(t)
-
Figura f-30
F - 31 En el circuito de la figura la resistencia de Thevenin entre los terminales 1 y 1´ es :
100K
1
ohms
a) 90 ohms
100i
b) 1100 ohms
c) 5030 ohms
10K
1K
i
1K
d) 17.5 kohms
+ Vg(t)
-
100
1´
Figura f-31
F - 32 En el circuito de la figura la resistencia de Thevenin entre los terminales del capacitor
es :
a) R1 + R2
R
1
b) (R1 + R2)/2
c) R1 + R2 // R3
Vo
R
R
d) 2 R1 + R2
C
3
1
+
Figura f-32
d(t) +
-
R
En el mismo circuito la respuesta al impulso es :
52
2
a)
b)
c)
d)
-t/T
Vg R2/R1 + R2 (-1/T e
u(t) +d(t))
-t/T
Vg (R2//R1)/R1//R2 + R1 (-1/T e
u(t) )
-t/T
Vg R2/R1 + R2 (-1/T e
u(t) )
-t/T
Vg 1/ 1+R2/R1 (-1/T e
u(t) + 2 Vg d(t))
F - 33 En el circuito de la figura la tensión sobre el capacitor 1 mseg. después de abrir la llave
es :
t = 1mseg
a) 0.216 V
b) 0.864 V
c) 1 V
d) 2.1 V
Vo(0) = 0
i(0) = 0
1mH
1K
ohms, henries, farads
+
i
u(t)
1µF
1K
Vo
-
Figura f-33
F - 34 Hallar el equivalente Norton visto entre los terminales 1 y 1´:[ I N // R N ]
0.04 Va
+ Va 1 ohms
R
1mA u(t)
R
R
R
R = 1K
1´
Figura f-34
F - 35 Graficar Vo(t).
1µF
ohms, farads
+
1mA u(t)
1K
Vo(t)
-
t = 2mseg.
1K
1µF
Figura f-35
F - 36 Obtener la respuesta al impulso en Vo
1K
ohms, farads
10K
1K
10K
+-
-
+
d(t)
1nF
Vo
+
100K
100K
Figura f-36
F - 37 En el circuito de la figura VC1(0) = VC2(0)= 0. La expresión de VO(t) es :
53
a)
b)
c)
d)
-6
-5
1.11 ( e -t / 10 - e -t / 10 )
-6
-5
-10 ( 1 - e -t / 10 - e -t / 10 )
-6
-5
11.1 ( e -t / 10 - e -t / 10 )
-6
- 10 ( e -t / 3 10 sen ( 2 _ 50 KHz t ))
En el mismo circuito, para que el transitorio sea nulo, VC1(0) VC2(0) deben ser :
a)
b)
c)
d)
+ Vc2 -
VC1(0) =
VC2(0) = 0
VC1(0) = 1V
VC2(0) = -1V
VC1(0) = - 1V
VC2(0) = 0
No hay juego de valores posibles
1 nF
1K
1 nF
-
10K
Vo(t)
Vc +
1
u(t) +-
Figura f-37
F - 38 La respuesta Vo(t) con condiciones iniciales nulas en los capacitores es :
a)
b)
c)
d)
-6
100pF
-7
11 ( 1 - e -t / 10 + e - t / 10 )
-6
u (t) ( 11 - e -t / 10 )
11 u(t)
-6
-10 u(t) ( 1 - 9 / 11 e -t / 10 )
10K
1K
Vo(t)
100pF
u(t) +-
Figura f-38
F - 39 La respuesta al escalón del circuito, con condiciones iniciales nulas en los capacitores
es :
1nF
-t / 10 -5
-t / 10 -4
)) u(t)
a) ( 2 + 10 / 9 ( e
-e
-t / 10 -5
-t / 10 -4
10K
)) u(t)
b) ( 1 + 10 / 9 ( e
-e
-t / 10 -5
c) ( 1 + 10 / 9 e
) u(t)
-t / 10 -4
-t / 10 -5
d) 10 / 9 ( e
-e
) u(t)
Vo(t)
10K
10nF
Figura f-39
54
u(t) +-
F - 40 La respuesta Vo(t) para t = 4 seg. es :
a)
b)
c)
d)
C
C R = 10s
1
1
C R = 0.1s
2
2
R =R
-0.32 V
-0.12 V
0.15 V
0.43 V
1
R
2
R
2
C
1
2
1
Vo(t)
u(t) - u(t-2) +-
Figura f-40
Graficar la respuesta completa
F - 41 La expresión de Vo(t) para Vi(t) = u(t) es :
-t
R
CR = 1s
- t / 10
a) ( e - 0.1 e
) u(t)
-t
b) (1 - e cos ( t + 45°)) u(t)
-t
c) (1 - t ) e u(t)
-t
d) d(t) + e u(t)
Vc(0) = 0
C
C
Vo(t)
u(t) +-
R
Figura f-41
F - 42 La respuesta al impulso V2(t) es :
a) d (t) - u (t)
-t
b) ( 1 - e ) u(t)
-t
c) ( e - 1) u(t)
-t
d) e cos ( t +_ / 2) u(t)
C
C R = C R =1s
1
1
2
2
R
2
1
Vo(t)
d(t) +-
C
1
Figura f-42
55
R
2
F - 42 Obtener la respuesta al impulso y al escalón del circuito de la figura. Graficar V2(t).
RC = 0.001s
R /R = 10
ohms, farads
1
R
Vi
+
-
C
R
1
R
Vo
C
R
R
Figura f-43
F - 44 Obtener la respuesta al impulso y al escalón del circuito de la figura :
Graficar ambas respuestas.
C
2R
R
Vo(t)
Vi +-
C/2
R
R
RC = 0.001s
Figura f-44
F - 45 Para ambos circuitos obtener:
C
a) La respuesta al impulso del
circuito.
b) La respuesta al escalón
R
R
Vo(t)
Vi +-
C
R
R
1pF
1M
Vg(t)
1nF
+
Va
-
ohms, farads
1K
1mA/V
Figura f-45
F - 46 En el circuito de la figura Vc1 (0) = Vc2(0) = 0.
56
Vo(t)
R = 1K
C = 1nF
a) Calcular Vo(t). V1(t) = 1V u(t)
R1 = 1K, R2 = 10K, C1 = C2 = 1nF
b) Determinar los valores de Vc1(0) y Vc2(0) para anular el transitorio en Vo(t).
c) Calcular Vo(t). V1(t) = u(t) - u(t-2)
R1C1 = 10s
R2C2 = 0.1s
+
Vc2
C
V1(t)
Vc1
C
+
-
1
2
R
+
R
ohms, farads
-
2
Vo(t)
1
Figura f-46
F - 47 Encontrar la respuesta Vo(t) con condiciones iniciales nulas en los capacitores, en los
siguientes circuitos :
1nF
100pF
ohms, farads
10K
10K
1K
Vo(t)
Vo(t)
100pF
+
-
10K
10nF
V (t)=u(t)
1
+
-
V (t)=u(t)
1
Figura f-47
F - 48 Encontrar Vo(t).
Vc (0) = 0
R
RC=1seg.
C
V (t)=u(t)
1
ohms, farads
ohms, farads
C
Vo(t)
+
-
R
Figura f-48
57
F - 49 Determinar la respuesta al impulso.
C
R1 C1 =R2 C2 =1seg.
R
V (t)=d(t)
1
ohms, farads
1
1
Vo(t)
+
-
C
2
R
2
Figura f-49
F - 50 Obtener y graficar la respuesta al escalón y al impulso de los siguientes circuitos :
C
ohms, farads
R1 /R=10
RC=10mseg.
R
Vo(t)
R
R
1
V (t)
1
R
C
+
-
R
(a)
C
RC=10mseg.
R
2R
V
V
1
+
-
2
C/2
R
R
(b)
Figura f-50
F - 51 En la red de la figura un generador de tensión V1 puesto en 1-1´produce una tensión V2
a circuito abierto en 2-2. La red es recíproca, esto significa :
a) Si se coloca un generador de tensión en 2-2´de valor V1 aparece una tensión a circuito
abierto en 1-1´de valor V2.
58
b)
Si se coloca un generador de tensión en 2-2´ de valor V1 aparece una corriente en
cortocircuito en 1-1´ de valor en módulo igual a V2.
c) Si se coloca un generador de corriente entre 2-2´ de valor en módulo igual a V 1 aparece una
corriente en cortocircuito en 1-1´ de valor en módulo igual a V2.
d) Si se coloca un generador de corriente entre 2-2´ de valor en módulo igual a V 1 aparece una
tensión a circuito abierto en 1-1´ de valor V2.
1
R
L
1
2
2´
C
R
1´
2
Figura f-51
F - 52 La respuesta al escalón V2(t) del circuito tendrá un transitorio nulo si :
a) iL (0) = 0
Vc(0) = 0
b) iL (0) = 0.5A
Vc(0) = 0
c) iL (0) = 0
Vc(0) = 0.5V
d) iL (0) = 0.5A
Vc(0) = 0.5V
ohms, henries, farads
1K
VC
V (t) +
1
-
iL
+
+
1µF
-
1K
V2 (t)
1mHy
-
Figura f-52
F - 53 Obtener la respuesta al impulso y al escalón del circuito de la figura.
1M
Vg(t)
ohms, farads
1pF
+
Vc
-
+
1nF
1K
1mA/V Vc
Figura f-53
59
Vo(t)
-