Curso: 2009 – 2010 Modelo: 6 Opción
Anuncio

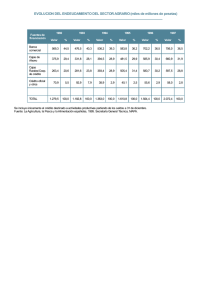
EJERCICIO RESUELTO DE SELECTIVIDAD (ANDALUCIA) Curso: 2009 – 2010 Modelo: 6 Opción: A Ejercicio: 1. ENUNCIADO: (2.5 puntos) Un supermercado se abastece de gambas y langostinos a través de dos mayoristas, A y B, que le envían contenedores con cajas completas de ambos productos. El mayorista A envía en cada contenedor 2 cajas de gambas y 3 de langostinos, al precio de 350 euros el contenedor, mientras que el mayorista B envía en cada uno 1 caja de gambas y 5 de langostinos, al precio de 550 euros el contenedor. El supermercado necesita, como mínimo, 50 cajas de gambas y 180 de langostinos pudiendo almacenar, como máximo, 50 contenedores. ¿Cuántos contenedores debería pedir el supermercado a cada mayorista paras satisfacer sus necesidades con el menor coste posible?. Indique cuál sería ese coste mínimo. RESOLUCIÓN: Ver página siguiente. 1 de 4 Resolución: Sea “x” el número de contenedores que el supermercado pide al mayorista A y sea “y” el número de contenedores que el supermercado pide al mayorista B. Conclusiones: “x” contenedores del tipo A, a 2 cajas de gambas cada uno, hacen un total de “x·2” cajas gambas. “y” contenedores del tipo B, a 1 caja de gambas cada uno, hacen un total de “y” cajas de gambas. Por las necesidades del supermercado es obligado que 2x + y 50 “x” contenedores del tipo A, a 3 cajas de langostinos cada uno, hacen un total de “x·3” cajas de langostinos. “y” contenedores del tipo B, a 5 cajas de langostinos cada uno, hacen un total de “y·5” cajas de langostinos. Por las necesidades del supermercado es obligado que 3x + 5y 180 También, por las necesidades del supermercado, es obligado que x + y 50 La resolución del sistema de inecuaciones: 2 x y 50 3x 5 y 180 x y 50 son los puntos (x , y) que ocupan el área del siguiente triángulo de vértices ABC y 50 B 36 A C 25 x 50 60 Recta 3x + 5y = 180 Recta x + y = 50 Recta 2x + y = 50 2 de 4 Y ahora vamos a calcular las coordenadas del punto A: 10 x 5 y 250 3x 5 y 180 3x 5 y 180 7x 70 2 x y 50 2 10 y 50 20 y 50 y 30 x 10 Las coordenadas del punto A son x 10 , y 30 Ahora vamos a calcular las coordenadas del punto C: 3x 3 y 150 3x 5 y 180 3x 5 y 180 2 y 30 x y 50 y x 15 50 x 50 15 x 35 30 2 y 15 Las coordenadas del punto C son x 35 , y 15 Ya tenemos totalmente descrita la región de validez, la cual es un triángulo de vértices x 10 , y 30 ; x 35 , y 15 ; x 0 , y 50 Una vez localizada la región de validez, ahora conviene definir la función COSTE, la cual es: Cx, y 350 x 550 y Para ver en qué punto, dentro de la región de validez, el valor de C x, y sea mínimo, habrá que evaluar dicha función en los vértices del mencionado triángulo. Empecemos: C 10,30 350 10 550 30 20000 C 35,15 350 35 550 15 20500 C 0,50 350 0 550 50 27500 La función C x, y , evaluada dentro de la región perteneciente al área del triángulo de vértices x 10 , y 30 ; x 35 , y 15 ; x 0 , y 50 , alcanza su mínimo valor en el punto . x 10 , y 30 . 3 de 4 Por todo esto, si el supermercado quiere satisfacer sus necesidades con el menor coste posible, tendría que pedir 10 contenedores al mayorista A y 30 contenedores al mayorista B, teniendo esto un coste de 20.000 euros. 4 de 4