TALLER 27

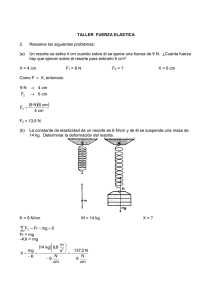
TALLER 27: FUERZAS ELÁSTICAS RECUPERADORAS
2.
Resuelve los siguientes problemas:
(a)
Un resorte se estira 4 cm cuando sobre él se ejerce una fuerza de 9 N. ¿Cuánta fuerza
hay que ejercer sobre el resorte para estirarlo 6 cm?
X = 4 cm
F1 = 9 N
F2 = ?
X = 6 cm
Como F  X, entonces:
9 N  4 cm
F2  6 cm
F2 
9 N6 cm
4 cm
F2 = 13,5 N
(b)
La constante de elasticidad de un resorte es 6 N/cm y de él se suspende una masa de
14 kg. Determinar la deformación del resorte.
K = 6 N/cm
F
Y
M = 14 kg
 Fr  mg  0
Fr = mg
–KX = mg
X
mg

K
14 kg 9,8

6
N
cm
m

s2 

137,2 N
N
6
cm
X=?
X = –22,87 cm = 0,23 m
(c)
Una masa de 5 kg descansa sobre un plano inclinado 30º respecto a la horizontal, sin
rozamiento, suspendido de un resorte, tal como se ilustra en la figura. Si el resorte se
ha alargado 8 cm, calcular la constante de elasticidad del resorte. Si la masa se
desplaza 8 cm por debajo de la posición de equilibrio y se deja en libertad, ¿cuál será
su aceleración?
F
F
X
 Fr  mgsen 30º  0
(1)
Y
 N  mgcos 30º  0
(2)
De la ecuación (1) se tiene que:
Fr = mg sen 30º
KX = mg sen 30
K
mgsen 30

X
K  306,25
5 kg 9,8
m
sen 30
s2 

0,08 m
N
m
Si la masa de desplaza 8 cm por debajo de la posición de equilibrio y se deja en libertad,
adquiere una aceleración:
F
F
X
 Fr  mgsen 30º  ma
Y
 N  mgcos 30º  0
(1)
(2)
De la ecuación (1) se despeja a:
a
Fr  mgsen 30 KX  mgsen 30 306,25  0,16  5  9,8  sen30


m
m
5
a = 4,9 m/s2
(d)
Demuestra que cuando dos resortes de constante de elasticidad k 1 y k2 se unen en
paralelo, la nueva constante del sistema es k =k1 + k2.
F
X
 F  Fr1  Fr2  0
F = Fr1+ Fr2
k.x = k1x + k2x
kx = (k1 + k2)x
De donde:
k = k1+ k2
(e) Demuestra que cuando dos resortes de constante de elasticidad k 1 y k2 se unen en serie,
k k
la nueva constante del sistema es: k  1 2
k1  k 2
Demostración:
La deformación total del sistema es:
x = x1 + x2 , donde:
x  x1  x 2 
1
F F
1

 F  
k1 k 2
 k1 k 2 
Como x 
F
k
1
F
1
1
 F   F   , entonces:
k
k
 k1 k 2 
1 1
1


k k1 k 2
1 k 2  k1

k k1  k 2
Por lo tanto:
k
k1  k 2
k1  k 2