TEOREMA DE ROLLE (I)

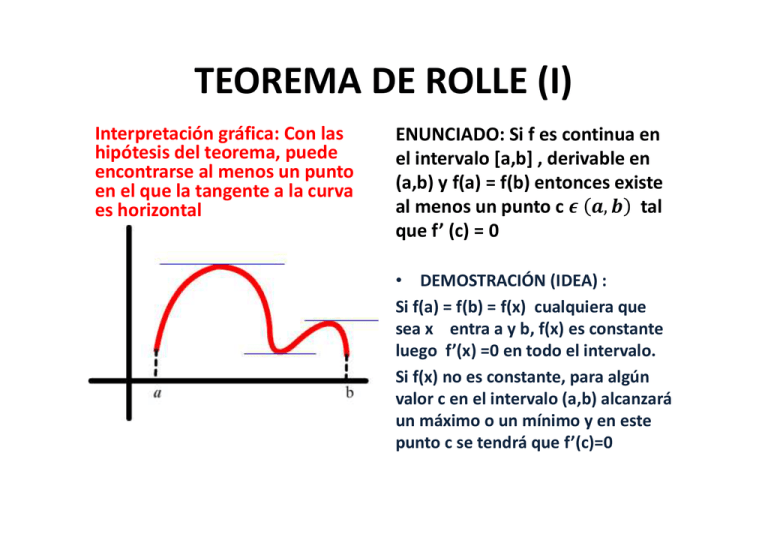
TEOREMA DE ROLLE (I)
Interpretación gráfica: Con las hipótesis del teorema, puede encontrarse al menos un punto en el que la tangente a la curva es horizontal
ENUNCIADO: Si f es continua en el intervalo [a,b] , derivable en (a,b) y f(a) = f(b) entonces existe al menos un punto c ,
tal que f’ (c) = 0
• DEMOSTRACIÓN (IDEA) :
Si f(a) = f(b) = f(x) cualquiera que sea x entra a y b, f(x) es constante luego f’(x) =0 en todo el intervalo.
Si f(x) no es constante, para algún valor c en el intervalo (a,b) alcanzará un máximo o un mínimo y en este punto c se tendrá que f’(c)=0
TEOREMA DE ROLLE (II)
¿Es necesaria la condición “derivable” en la hipótesis?
Consideremos la función f(x) = |x| en el intervalo [‐1,1].
La función es continua pero no es derivable en x = 0 . La derivada nunca se anula Ya que:
1 f’ (x) = 1 0
0
APLICACIÓN
Prueba que con independencia del valor de a, la ecuación no puede tener dos soluciones distintas entre ‐2 y 2.
SOLUCIÓN La función cumple las hipótesis del teorema de Rolle por ser un polinomio. Si tuviese dos soluciones distintas a y b entre 2 y ‐2,
f(a) = f(b) = 0 y [a,b] C [‐2,2] luego por el teorema de Rolle la derivada se anula en c , ‐2 ≤ a < c < b ≤ 2. Ahora bien, f’(x) = TEOREMA DEL VALOR MEDIO (I)
INTERPRETACIÓN GEOMÉTRICA
Si f(x) cumple las hipótesis del teorema del valor medio, existe al menos un punto entre a y b tal que la tangente a la curva en x = c es paralela a la secante que une los puntos (a, f(a)) y (b,f(b))
ENUNCIADO
Si f(x) es continua en [a,b] y derivable en (a,b) entonces existe c , tal que:
f’ (c) = TEOREMA DEL VALOR MEDIO (II)
Si f(x) es continua en [a,b] y derivable en (a , b) entonces existe c ( a, b) tal que f’ (c) = DEMOSTRACIÓN Definimos g(x) = f(x) (x – a) + f(a)
g(x) es continua en [a,b] y derivable en (a,b) porque es la diferencia entre f(x) y una recta ( secante en x=a y x = b)
Se puede comprobar que g(a) = g(b) = 0. Aplicando el teorema de Rolle , existe c (a,b) tal que g’ (c) = 0 g’(x) = f’(x) ‐
; g’(c) = 0 = f´(c) ‐
TEOREMA DEL VALOR MEDIO (III)
• Dada f(x) = 5 ‐
, halla todos los valores que cumplan el TVM en el intervalo (1, 4).
• SOLUCIÓN
El único punto conflictivo de f(x) es x = 0 que no pertenece a ( 1, 4).Se cumplen las hipótesis del TVM y f’ (x) = = Resolvemos la ecuación y c = 2, ‐2 luego la única solución es c = 2
TEOREMA DEL VALOR MEDIO (IV)
Dos coches patrulla están situados a una distancia, uno de otro, de 8 Km en una autopista. Cuando un camión pasa junto a uno de ellos se le mide una velocidad de 80 Km/h y cuatro minutos más tarde, el segundo coche patrulla mide una velocidad de 90 Km/h. Prueba que en algún momento el camión ha sobrepasado la velocidad límite de 100 Km/h y puede ser multado
SOLUCIÓN Si t = 0 es el tiempo en el que pasa junto al primer coche patrulla, s = 4 minutos = 1/15 h es cuando pasa por el segundo control. Si s(t) es la función que da la distancia recorrida, s(1/15) – s(0) = 8
1/15 – 0 = 1/15. Por el teorema del valor medio en algún momento c entre 0 y 1/15, s ‘(c) =
= 120 Km/h
/
TEOREMA DEL VALOR MEDIO GENERALIZADO (CAUCHY)
Si f(x) y g(x) son funciones continuas en [a,b], derivables en (a,b) y g’(x) ≠0 en (a,b) , entonces existe un número c (a,b) tal que :
Nota 1 : Podemos asumir que g(a) ≠g(b) ya que en otro caso, por el teorema de Rolle, g’(a) = 0 para algún valor entre a y b
Nota 2: = k ; f’(c) = kg’(c) . La interpretación geométrica es que si f(x) y g(x) cumplen las hipótesis, para algún punto c entre a y b podemos encontrar una recta tangente a f cuya pendiente es k veces la de la tangente a g..
Demostración del teorema de Cauchy
Definimos la función h(x) = f(x) – kg(x) donde k = .
h(x) es continua en [a,b] y derivable en (a,b) por ser la diferencia
de dos funciones que cumplen estas hipótesis ( k es una constante). Comprobamos que h(x) cumple el teorema de Rolle:
h(a) = f(a) g(a) = (reduciendo a común denominador)
= De manera análoga, h(b) =
. Aplicamos el teorema de Rolle : existe c entra a y b para el que h’ (c) = 0 ; h´(x) = f’(x) – k g’(x) ;
h’(c) = f’ (c) – kg’ (c) = 0 ; despejando : k = = REGLA DE L’HÔPITAL
Sean f(x) y g(x) funciones derivables en un intervalo ( a, a+r) , que g’(x) ≠ 0 en ese intervalo, que y que →
→
→
= L , entonces →
= L .
Demostración: Definimos G(x) = = F(x) y G(x) cumplen las hipótesis del teorema del valor medio generalizado en un intervalo [a,x] con a < x < a+r . Existe pues c entre a y x tal que
F(x) = ; como F(a) = G(a) = 0 y F(x) =f(x) y G(x) = g(x) para x≠ a , queda ; ahora, si x tiende a a , c que está entre a y x también tiende a a ( por la dcha) y el resultado se tiene,
Obviamente, igual razonamiento con límite por la izquierda y límite global.
APLICACIÓN 1
→
(indeterminación 0/0)
; en un intervalo abierto suficientemente pequeño centrado en 1, lnx y son continuas y derivables y (lnx)’ = 1/x no se anula.
→
→
→
→
⁄
→
= ½
CONSIDERACIONES SOBRE LA REGLA DE L’HÔPITAL
1 La regla de L’Hôpital es válida para indeterminaciones del tipo . 2 La regla de L’Hôpital es válida para indeterminaciones del tipo 0. ∞ ( SI → → ∞,
.
que es ahora una indeterminación del tipo 0/0)
3 Si el límite del cociente de derivadas nos vuelve a dar una indeterminación, reiteramos el proceso, es decir :
→
→
→
etc