Razonamiento Lógico

1
IDEPUNP/CICLO REGULAR /ABRIL– JULIO 2016
RAZONAMIENTO LÓGICO
SEMANA Nº 04
TEMA: EQUIVALENCIAS I
COORDINADOR: DENISSE MORANTE SAMANIEGO.
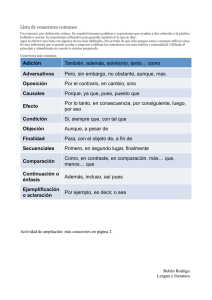
DEDUCCIONES INMEDIATAS
c)LEYDISTRIBUTIVA:(Solo se distribuye los conectores
Son razonamientos que partiendo de una sola premisa se
combinados , ,  ,   )
deduce la conclusión aplicando las equivalencias lógicas.
Esta ley consiste en repartir la proposición externa a cada
Ejemplo: Es falso que ni trabaja ni estudia
una de las proposiciones internas.
Luego, trabaja o estudia
1) A   B  C    A  B    A  C 
EQUIVALENCIAS LOGICAS
Son un conjunto de identidades que permiten simplificar o
transformar esquemas lógicos en otros equivalentes.
EQUIVALENCIAS NOTABLES
Son las diferentes leyes lógicas donde al unirlas por el
bicondicional
"  ", se obtiene una tautología. Dos
esquemas moleculares, por ejemplo A y B son equivalentes
cuando unidos por el bicondicional “  ” el resultado es una
2) A   B  C    A  B    A  C 
3) A  B  C    A  B    A  C 
4) A  B  C    A  B    A  C 
Ejemplo: Los sabios dicen la verdad; sin embargo, tienen
problemas con la sociedad o la religión los condena
Equivale a: Los sabios dicen la verdad y tienen problemas
con la sociedad; o los sabios dicen la verdad y la religión
los condena.
Simbólicamente: A   B  C    A  B    A  C 
d) LEY DE ÍDEMPOTENCIA:Por esta ley se reducen las
tautología.
LEYES DE EQUIVALENCIA
variables repetidas a una sola. Se aplica a esquemas
Sean A, B y C proposiciones cualesquiera:
conjuntivos y disyuntivos.
a)LEY CONMUTATIVA:Esta ley nos indica que todos los
1) A  A  A
2) A  A  A
conectores a excepción de la condicional (implicador y
replicador), si se cambian de orden sus componentes, sus
equivalentes significan lo mismo. .
1)
2)
3)
4)
5)
6)
A B B  A
AB B A
A B  B A
A B B A
A B B A
A BB A
Ejemplo: Jaqueline enseña Algebra y Rosa enseña lógica.
Equivale a: Rosa enseña lógica y Jaqueline enseña
Algebra.
Simbólicamente: A  B  B  A
b) LEYASOCIATIVA:(esta ley se cumple solo con los
conectores ,  , ,  )
Esta ley nos indica que cuando los conectores son iguales
estos se pueden agrupar mediante símbolos de agrupación
“( ), { }, [ ].
1)  A  B   C  A  B  C 
2)  A  B   C  A  B  C 
3)  A  B   C  A  B  C 
4)  A  B   C  A  B  C 
Ejemplo:
María enseña lógica y geometría, sin embargo estudia
economía.
Equivale a:
Ejemplo: Piura es la ciudad del eterno calor y Piura es la
ciudad del eterno calor.
Equivale a: Piura es la ciudad del eterno calor.
Simbólicamente: A  A  A
e)LEY DE LA INVOLUCIÓN (DOBLE NEGACION):Esta
ley consiste en agregar o quitar negaciones de manera par.
1)    A   A .
Ejemplo: Es absurdo que Luis no sea de Tarapoto.
Equivale a: Luis es de Tarapoto.
Simbólicamente:    A   A
f) LEY DE D MORGAN: (solo se aplica con los conectores
,  ).
Son equivalencias de esquemas conjuntivos y disyuntivos.
Conjunciones no negadas son equivalentes a disyunciones
negadas y viceversa.
1) A  B     A   B 
2) A  B     A   B 
3)   A  B    A   B 4)   A  B    A   B
Ejemplo: Es inconcebible
que Alex
sea honrado
y
trabaje.
Equivale a: Alex no es honrado y no trabaja.
Simbólicamente:   A  B    A   B
María enseña lógica, sin embargo enseña geometría y
estudia economía.
g) LEY DE CONTRAPOSICION O CONTRARRECIPROCA
Simbólicamente:  A  B   C  A  B  C 
(solo se aplica con los conectores logicos →, ←)
IDEPUNP/CICLO REGULAR /ABRIL– JULIO 2016
Se conmutan las variables manteniendo las flechas en su
misma dirección y negando ambas variables.
1) A  B   B  A
2) A  B   B  A
h)DEFINICIÓN DE IMPLICADOR: Se niega el antecedente
y el conector lógico (  ) se cambia por el conector lógico (
 ) y el consecuente se repite.
1) A  B   A  B
2) A  B    A   B 
i) LEYES DE ABSORCION (Solo se utiliza con los
conectores combinados ,   )
I) Primera ley de absorción:
 Conectores combinados ,  
 Termino externo repetido
 Conclusión : Solo el término que se repite el otro
se elimina
1) A   A  B   A
2) A   A  B   A
II) Segunda ley de absorción:
 Conectores combinados ,  
 Termino externo con su opuesto
 Conclusión: Toda la parte externa y la parte no
común.
1) A    A  B   A  B
2) A    A  B   A  B
j)LEY DE COMPLEMENTO:Se utiliza para proposiciones
opuestas por su signo.
1) A   A  V
2) A   A  F
3)  V  F
4)  F  V
k) LEY DEIDENTIDAD:Una proposición cualquiera llamada
“A” es ordenada al lado de una tautología (V ó 1) o una
contradicción (F ó 0).
1) A  F  A
2) A  V  V
3) A  F  F
4) A  V  A
l) FLECHA DE NICOD
AB  A  B
m) BARRA DE SHAFFER
A B  A  B
n)LEY DE MUTACION
A  (B  C )  B  ( A  C )
ñ) LEY DE EXPORTACION
( A  B)  C  A  (B  C )
O) LEY DE EXPANSION




A  [ A  ( B   B]
A  B  [  A  ( A  B )]
A  [ A  ( B   B )]
A  B  [  A  ( A  B )]
2
RAZONAMIENTO LÓGICO