guia 8 2014

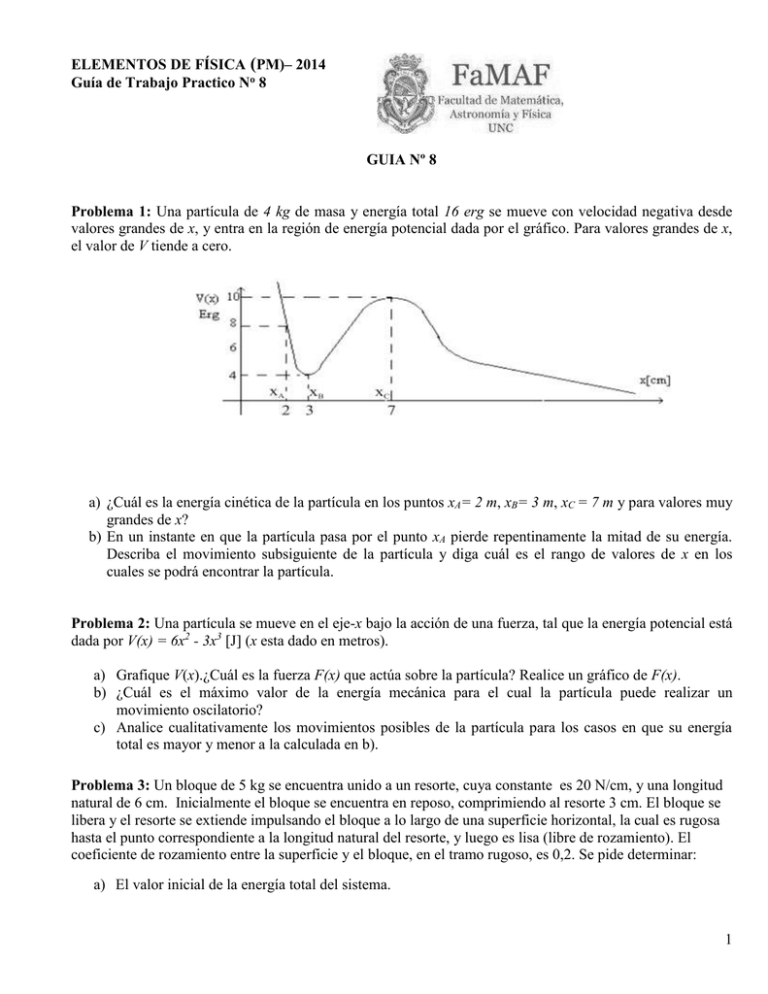
ELEMENTOS DE FÍSICA (PM)– 2014
Guía de Trabajo Practico No 8
GUIA Nº 8
Problema 1: Una partícula de 4 kg de masa y energía total 16 erg se mueve con velocidad negativa desde
valores grandes de x, y entra en la región de energía potencial dada por el gráfico. Para valores grandes de x,
el valor de V tiende a cero.
a) ¿Cuál es la energía cinética de la partícula en los puntos xA= 2 m, xB= 3 m, xC = 7 m y para valores muy
grandes de x?
b) En un instante en que la partícula pasa por el punto xA pierde repentinamente la mitad de su energía.
Describa el movimiento subsiguiente de la partícula y diga cuál es el rango de valores de x en los
cuales se podrá encontrar la partícula.
Problema 2: Una partícula se mueve en el eje-x bajo la acción de una fuerza, tal que la energía potencial está
dada por V(x) = 6x2 - 3x3 [J] (x esta dado en metros).
a) Grafique V(x).¿Cuál es la fuerza F(x) que actúa sobre la partícula? Realice un gráfico de F(x).
b) ¿Cuál es el máximo valor de la energía mecánica para el cual la partícula puede realizar un
movimiento oscilatorio?
c) Analice cualitativamente los movimientos posibles de la partícula para los casos en que su energía
total es mayor y menor a la calculada en b).
Problema 3: Un bloque de 5 kg se encuentra unido a un resorte, cuya constante es 20 N/cm, y una longitud
natural de 6 cm. Inicialmente el bloque se encuentra en reposo, comprimiendo al resorte 3 cm. El bloque se
libera y el resorte se extiende impulsando el bloque a lo largo de una superficie horizontal, la cual es rugosa
hasta el punto correspondiente a la longitud natural del resorte, y luego es lisa (libre de rozamiento). El
coeficiente de rozamiento entre la superficie y el bloque, en el tramo rugoso, es 0,2. Se pide determinar:
a) El valor inicial de la energía total del sistema.
1
b) La variación de la energía total del sistema entre el instante inicial y el momento en que el bloque
pasa por la posición correspondiente a la longitud natural del resorte.
c) La velocidad del bloque al pasar por dicha posición.
d) El máximo estiramiento que alcanzará el resorte.
e) Realizar un gráfico de energía vs. posición, tomando como cero del eje de coordenadas el punto
correspondiente a la longitud natural del resorte, y en el mismo graficar las funciones energía total y
energía potencial del sistema. Indique en este gráfico el punto donde el resorte tiene el máximo
estiramiento. ¿Es posible estimar cuál será la posición en la que el bloque se detendrá cuando vuelva
a comprimir el resorte?
2