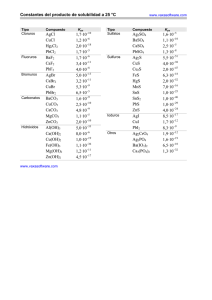
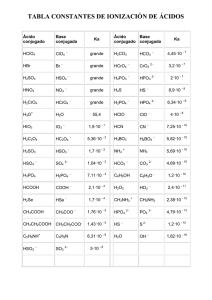
γ γ γ γ (1 )

ANÁLISIS DE DESVIACIONES PATOLÓGICAS DE LA LEY DE RAOULT.
Para una mezcla binaria se define :
(1  x2 )
d ln  1
d ln  2
 x2
dx2
dx2
donde :
1 
p1
(1  x2 ) p o1
2 
p2
x2 p o 2
GE
 (1  x2 ) ln  1  x2 ln  2
RT
 GE 
d


RT 
 GE 

ln  1  
  x2
dx
 RT 
 GE 
d


RT 
 GE 

ln  2  
  (1  x2 )
dx
 RT 
GE
 x2 (1  x2 )  A  B (1  2 x2 )  C (1  2 x2 ) 2  ...
RT
ln  1  x2 2  ( A  B  C )  (4 B  16C ) x2  12Cx2 2 
ln  2  (1  x2 ) 2 ( A  B  C )  (4 B  8C ) x2  12Cx2 2 
CASO I.
A = B =C = 0 ; GE / RT = 0 ; ln γ1 = 0 ; ln γ2 = 0
P1 = ( 1 – x2 )Po1
P2 = x2 Po2
CASO II
MEZCLAS REGULARES
B=C=0
Se forma un compuesto 1:1 en equilibrio con los otros componentes
GE
 Ax2 (1  x2 ) ;
RT
ln  1  Ax2 2 ;
ln  2  A(1  x2 ) 2
A=1 ; B=C=0
Ln γ 2
Ln γ 1
GE / RT
P2 / Po2
X1
X1
Desviaciones positivas de la Ley de Raoult
A = -1 ; B=C = 0
P1/ PO1
GE/R
Ln γ 2
Ln γ 1
X2
X1
Desviaciones Negativas de la ley de Raoult
CASO III :
B=-A
Y C=0
GE
 2 Ax2 2 (1  x2 )
RT
;
ln  1  2 Ax2 2 (2 x2  1) ; ln  2  4 A(1  x2 ) 2 x2
Sistemas: C2 H 5OH  CHCl3 A 35O C ; AgCl – NaCl a 150o C ; C5H5N-H2O
A = 1 ; B = -1 ; C = 0
Ln γ 1
o
P2 / P 2
GE / RT
Ln γ2
o
P1 / P 1
o
P1/ P 1
o
P2/ P 2
G / RT
Ln γ 2
A =1 ; B = 1 ; C = 0
SE FORMAN COMPUESTOS 1:2
CH3NO2 – (C2H5)2 O , a 45 o C ; Ta – Hg a 325 o C ; Cd – Sb a 480 o C
Zn – Sb a 550 o C ; K – Hg a 275 o y 325 o C ;
soluciones sólidas: PbBr2 – PbCl2 a 200 o C
CASO IV.
A=0 ; C=0
GE
 Bx2 (1  x2 )(1  2 x2 ) ; ln  1  Bx2 2 (3  4 x2 ) ; ln  2  B (1  x2 ) 2 (1  4 x2 )
RT
Ln γ2
E
G
/ RT
Ln γ1
A=0;B=1;C=0
Soluciones sólidas de p-dicloro benceno – p- dibromo benceno a 50 o C
CASO V.
B=0;C= -A
GE
 4 Ax2 2 (1  x2 )2 ; ln  1  4 Ax2 2 (1  x2 )(3x2  1) ; ln  2  4 A(1  x2 ) 2 x2 (2  3 x2 )
RT
Ln γ 2
Ln γ 1
G
E
/ RT
Benceno-bromobenceno a 80o C ; Cd – K a 475 oC
A=1;B=0;C=-1
E
G
/ RT
o
P1 / P 1
Ln γ 1
Ln γ2
A = -1 ; B = 0 ; C = 1
Bi – Cd a 431, 477, 500 y 533 o C
Pb – Tl a 438 o C
o
P2 / P 2