Tutorial Simulaciones

Recomendaciones y conceptos adicionales para la
realización de los TPs
Notas para la práctica de los miércoles - 66.78 - FIUBA
Andrés Altieri
Juan Augusto Maya
2 de diciembre de 2013
1.
Vectorización del código
En algunos lenguajes, como en C, las operaciones sobre vectores se realizan recurriendo a
construcciones iterativas como los ciclos for, while, etc. y para la evaluación de condiciones lógicas se recurre normalmente a contrucciones de tipo if/then/else, etc. En Matlab, estas construcciones existen, pero para muchas operaciones sobre vectores existen funciones optimizadas que
tienen un tiempo de ejecución notablemente menor que sus contrapartes iterativas o lógicas.
Por ejemplo, supongamos que tenemos dos vectores, x e y que queremos comparar, generando un tercer vector booleano out de modo que:
(
true si x(i) = y(i)
out(i) =
.
false en otro caso
Un implementación en Matlab de este código usando ciclos for serı́a:
out = false ( s i z e ( x ) ) ; % r e s e r v a de memoria para a h o r r a r tiempo
f o r n0 = 1 : l e n g t h ( x ) % para cada componente de l o s v e c t o r e s
i f x ( n0 ) == y ( n0 )
% comparo
out ( n0 ) = true ;
end
end
Una implementación de estas caracterı́sticas es adecuada para un lenguaje como C. En Matlab,
podemos recurrir al operador ==, que compara componente a componente dos vectores y devuelve un nuevo vector con unos en las posiciones donde cumpla la condición lógica. El programa anterior en una implementación eficiente serı́a:
out = ( x == y ) % l o s p a r é n t e s i s no son n e c e s a r i o s
Esto no sólo es más compacto y comprensible sino mucho más rápido. Lo mismo podrı́a hacer
con >, <, >=, ∼= etc. o con cualquier otra condición lógica.
Por otro lado, la mayorı́a de las funciones de Matlab u Octave admiten ser llamadas en forma
vectorial. Siempre debemos tener en cuenta esto ya que utilizar en forma repetida las funciones
mediante un ciclo for introducirá demoras inaceptables (además hacer el código más largo y
difı́cil de leer). Por ejemplo:
N = 1e5 ;
% c a n t i d a d de v a r i a b l e s a g e n e r a r :
% Hacer a s i :
x = randn ( 1 , N ) ; % Genero un v e c t o r de v a r i a b l e s N( 0 , 1 ) de tama ño 1xN
% y nunca a s i :
1
66.78 - Comunicaciones Digitales y Analógicas
Sugerencia para los TPs - Curso Miércoles
x = zeros ( 1 , N ) ;
f o r n0 = 1 : N
x ( n0 ) = randn ;
end
Por otro lado, en lenguajes donde los ciclos tipo for son la herramienta básica para iterar
se acostumbra repetir muchas veces una secuencia de instrucciones diferentes. Por ejemplo, supongamos que queremos generar una secuencia aleatoria de largo n de números enteros en el
intervalo 1, . . . , M y a cada uno de esos números sumarles una variable Gaussiana de media 0 y
varianza 1. Habitualmente podrı́a implementarse algo asi:
n = 1e5 ;
% c a n t i d a d de v a r i a b l e s a g e n e r a r :
out = z e r o s ( 1 , n ) ;
% Lento
f o r n0 = 1 : n
% cada i t e r a c i ó n genera uno de l o s r e s u l t a d o s f i n a l e s
out ( n0 ) = randi ( M ) ;
out ( n0 ) = out ( n0 ) + randn ; % podrı́a j u n t a r l o s dos pasos en uno
end
% Rapido
out = randi ( 1 , n , M ) ; % genero todos l o s e n t e r o s j u n t o s
out = out + randn ( 1 , n ) ; % sumo l a s normales j u n t a s
% Rapido y compacto
out = randi ( 1 , n , M ) + randn ( 1 , n ) ;
En general debemos intentar usar un código vectorizado para las tareas que sean más intensivas computacionalmente, reservando los ciclos for para operaciones que se repitan pocas veces.
Por ejemplo, si queremos evaluar simular la probabilidad de error de un sistema de comunicaciones para distintos valores de relación señal a ruido (SNR) usualmente requeriremos realizar,
para cada SNR, muchas corridas (ver la sección de Montecarlo). En ese caso podemos recorrer el
vector de SNRs con un for y vectorizar el código dentro del mismo:
SNRs = 2 : 2 : 1 0 ; % SNRs 2 , 4 , 6 , 8 , 1 0 dB
Pes = z e r o s ( s i z e ( SNRs ) ) ; % p r o b a b i l i d a d de e r r o r de sı́mbolo
f o r n0 = 1 : l e n g t h ( SNRs )
% codigo v e c t o r i z a d o
...
Pes ( n0 ) = . . .
end
En general, habrá un compromiso en la vectorización del codigo y la utilización de un código
tradicional. Podemos mencionar cuatro aspectos principales a evaluar:
Velocidad de ejecución.
Recursos de memoria.
Tiempo de desarrollo.
Legibilidad del código y robustez frente a errores de programación.
El código vectorizado en general va a ser más rápido y va a requerir más memoria. La utilización de la memoria no va a ser, por lo menos en este curso, un factor a tener cuenta por
el tipo de simulaciones que realizaremos, aunque en otro escenarios sı́ puede afectar. Desde un
punto de vista de tiempo de desarrollo, en general es más rápido implementar el código vectorizado una vez que se tiene un poco de práctica. Superado cierto umbral, aumenta la dificultad
de implementación en general. Por ejemplo, en el ejemplo anterior podrı́amos vectorizar simultaneamente todas las corridas para todos los valores de SNR, evitando el ciclo for externo, pero
probablemente serı́a más complicado y no se ganarı́a en términos de tiempos de ejecución.
2
66.78 - Comunicaciones Digitales y Analógicas
2.
Sugerencia para los TPs - Curso Miércoles
Métodos Montecarlo
Los métodos Montecarlo son, en forma amplia, un conjunto de algoritmos computacionales
que se basan en repetir un número grande de veces un experimento mediante muestreo aleatorio, con el objetivo de aproximar numéricamente la solución a un problema. Se utilizan muchas
veces cuando no existe una forma simple o una expresión cerrada que pueda implementarse para resolver un problema. Algunos de estos ejemplos son: resolver integrales multidimensionales,
optimización numérica, estimación de parámetros o muestreo de distribuciones de probabilidad.
Uno de los pilares fundamentales de los métodos Montecarlo son las llamadas leyes de los
grandes números. La ley de débil de los grandes números, enunciada a continuación es una de
las más importantes:
Teorema 2.1 (Ley débil de los grandes números). Sean X1 , X2 , . . . variables aleatorias independientes
idénticamente distribuidas, con media µ y sea:
n
X̄n =
1X
Xi
n i=1
la media muestral de las variables. Entonces, para cada > 0 tenemos:
lı́m P |X̄n − µ| > = 0.
n→∞
Este resultado implica que cuantas más realizaciones de las variables se promedien, menos
probable será que el valor que se obtenga esté alejado de la media verdadera µ. Es decir, que
repitiendo muchas veces un experimento y promediando podemos obtener un estimado de µ
que será bueno con una alta probabilidad.
Si se asume que las variables tienen varianza finita σ 2 , la prueba es muy simple usando la
desigualdad de Chebyshev:
V[X̄n ]
σ2
P |X̄n − µ| > ≤
=
−→ 0,
n n→∞
donde usamos que la varianza de X̄n es:
#
n
σ2
1X
Xi =
.
V[X̄n ] = V
n i=1
n
"
Dicha cota también nos da una idea (muy conservativa) de cuántas realizaciones debemos
promediar para que el estimador sea exacto con alta probabilidad. En particular, cuanto más
chico sea más debemos promediar.
En el curso se trabajará, en general, con el caso particular en el que las variables Xi son variables Bernoulli, es decir,
(
1 con probabilidad p
Xi =
.
0 con probababilidad 1 − p
El evento Xi = 1 puede representar un error en la transmisión de un sı́mbolo. Dichas variables
satisfacen:
E[Xi ] = p,
V[Xi ] = p(1 − p),
y por lo tanto lo que desearemos estimar es la probabilidad de error al enviar un sı́mbolo, es
decir, p. Es claro que cuanto más chico sea p, más grande deberá ser n para que la estimación se
aceptable. Por ejemplo si p = 0,001 y realizamos n = 10 experimentos, dificilmente observemos
un error dado que en promedio hay un error cada mil experimentos. Existen muchas cotas que
3
66.78 - Comunicaciones Digitales y Analógicas
Sugerencia para los TPs - Curso Miércoles
permiten estimar cuánto deberı́a ser n para garantizar que la probabilidad de que el estimador
sea malo sea muy pequeña. De hecho una cota muy holgada puede derivarse usando justamente
la desigualdad de Chebyshev. No entraremos en detalle en este análisis, sino que nos conformaremos con considerar como una regla práctica que n debe ser al menos un orden de magnitud
más grande que 1/p.
La ley débil de los grandes números puede extenderse para obtener la llamada ley fuerte de
los grandes números que dice que la convergencia a la media es con probabilidad uno y no sólo
en probabilidad. Para más detalles ver [1].
A continuación mencionamos dos ejemplos de utilización de los métodos Montecarlo para
ilustrar la ley de los grandes números y las ventajas de vectorizar el código. El segundo ejemplo
servirá de base para la implementación de los trabajos prácticos.
Ejemplo 2.1 (Estimación de π). Supongamos que queremos estimar el número π mediante un
método Montecarlo. Usamos un generador de números aleatorios que genera variables aleatorias Zi bidimensionales en el cuadrado (−1, 1) × (−1, 1). Trazamos un cı́rculo de radio R = 1
centrado en el origen de coordenadas. Sabemos que la probabilidad de que una variable de las
mencionadas caiga dentro del cı́rculo será:
πR2
π
Area circunferencia
= 2 = .
Area total
2
4
Usando las variables Zi definimos una nuevas variables Bernoulli:
P(||Zi || < 1) =
Xi = 1{||Zi || < 1}
de modo que:
P(Xi = 1) = P(||Zi || < 1) = π/4 = E[Xi ].
Si generamos n variables Xi independientes y calculamos:
n
X̄n =
1X
# de veces que Zi cayó en el cı́rculo
Xi =
.
n i=1
# total de experimentos
(1)
Aplicando la ley de los grandes números tenemos que:
π
lı́m P |X̄n − | > = 0.
n→∞
4
De esta forma podemos realizar el experimento, y utilizar la realización de 4X̄n para estimar la
constante π.
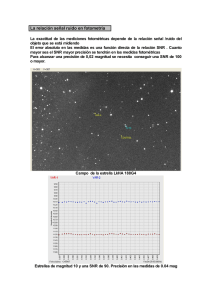
Por ejemplo, consideremos la Figura 1, donde podemos ver una realización del experimento.
Las cruces son las posiciones de las variables Zi . Tenemos n = 1000 experimentos y contamos
que m = 793 cayeron dentro del cı́rculo, es decir que podemos estimar:
π≈4
793
= 3,172.
1000
(2)
Es claro que tomando un n más grande alcanzaremos en general mayor exactitud en nuestra estimación. En la Figura 2 puede verse cómo evoluciona 4x̄n para una realización conforme
vamos agregando muestras, comparado contra el verdadero valor de π.
Veamos ahora como implementar esto en Matlab u Octave de modo rápido. A continuación
puede verse una implementación del estimador de π hecho en Matlab sin utilizar código vectorizado:
n = 1e5 ;
% c a n t i d a d de c o r r i d a s a promediar
X = zeros ( 1 , n ) ;
Xbarra = z e r o s ( 1 , n ) ;
4
66.78 - Comunicaciones Digitales y Analógicas
Sugerencia para los TPs - Curso Miércoles
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
−1
−0.5
0
0.5
1
Figura 1: Estimación de π. Evolución del estimador (1) con el número de promedios n para una
corrida.
3.3
3.25
3.2
3.15
3.1
3.05
3
1
2
3
4
5
n
6
7
8
9
10
4
x 10
Figura 2: Una realización del experimento para estimar π. La fracción de cruces dentro del cı́rculo
nos permite estimar dicho número.
f o r n0 = 1 : n
Z = [ rand rand ] * 2 − 1 ; % una r e a l i z a c i o n de l a v a r i a b l e Z
X = 0;
i f norm ( Z ) < 1
X = 1;
% una r e a l i z a c i o n de l a v a r i a b l e X
end
i f n0 == 1
Xbarra ( n0 ) = X ;
else
Xbarra ( n0 ) = ( Xbarra ( n0−1) * ( n0−1) + X ) /n0 ; % usa poca memoria
end
end
Se utilizan ciclos for para ir generando una a una las variables Xi y calculando en forma recursiva
el vector con la media muestral. A continuación puede verse una implementación vectorizada del
código:
5
66.78 - Comunicaciones Digitales y Analógicas
n = 1e5 ;
Sugerencia para los TPs - Curso Miércoles
% c a n t i d a d de c o r r i d a s a promediar
Zx = rand ( 1 , n ) * 2 − 1 ; % coordenada en x de l a s v a r i a b l e s Z
Zy = rand ( 1 , n ) * 2 − 1 ; % coordenada en y de l a s v a r i a b l e s Z
Xbarra = cumsum ( Zx . ˆ 2 + Zy . ˆ 2 < 1 ) . / ( 1 : n ) ; % media mu e s t r a l acumulada
La diferencia principal es que mientras en la versión con iteraciones se van generando una a
una las variables y actualizando la media muestral, en la versión vectorizada se realizan todas las
operaciones al mismo tiempo. Esto lleva a un código mucho mas compacto, elegante, con menor
cantidad de errores, y que en Matlab y Octave se ejecutan mucho más rápido. La desventaja
podrı́a ser que require un poco más de memoria ya que se generan todas las variables Zi al
mismo tiempo, pero esto no es problema en la mayorı́a de los casos.
Para ver las ventajas en términos de tiempo, 50 corridas de ambas rutinas arrojan un tiempo
promedio de 0,2992s para la rutina no vectorizada contra 0,0031s para la vectorizada, es decir, la
diferencia es de dos órdenes de magnitud.
Ejemplo 2.2 (Probabilidad de error de una M-PAM). El siguiente script de ejemplo calcula la
probabilidad de error de bit y de sı́mbolo para una constelación M -PAM y realiza los gráficos
correspondientes de las curvas.
clear
close a l l
clc
%% Parametros de a j u s t e de l a s i m u l a c i o n
M = 2;
% c a n t i d a d de simbolos
k = l o g 2 ( M ) ; % b i t s por simbolo
SNRbdB = 2 : 1 4 ; % SNR por b i t en dB
nsimbs = 2e6 ; % c a n t i d a d de simbolos que para cada v a l o r de SNRbdB en e l Montercarlo
%% Conversiones e i n i c i a l i z a c i o n e s v a r i a s
SNRbveces = 1 0 . ˆ ( SNRbdB /10) ; % SNR por b i t en v e c e s
SNRdB = SNRbdB + 10 * l o g 1 0 ( k ) ;
% SNR en dB
SNR = 1 0 . ˆ ( SNRdB /10) ;
% SNR en v e c e s
Eavg = 1 ;
Pes = z e r o s ( s i z e ( SNRbdB ) ) ;
Peb = z e r o s ( s i z e ( SNRbdB ) ) ;
% p r o b a b i l i d a d de e r r o r por simbolo simulada
% p r o b a b i l i d a d de e r r o r de b i t simulada
%% P ( e r r o r ) t e o r i c a :
% P r o b a b i l i d a d de e r r o r de b i t t e o r i c a de una 4−PAM
% Uso un puntero a una f u n c i o n cuyo parametro es SNR ( en v e c e s )
Pet = @ ( SNR ) 2 * (1−1/M ) * qfunc ( s q r t ( 3 * SNR /( Mˆ2 −1) ) ) ;
%% Simulacion Montecarlo
% Genero un o b j e t o ”modulador PAM” con M = 4 , codigo Gray y l a e s p e c i f i c o
% por su e n e r g i a promedio Eavg ( d e f i n i d a mas a r r i b a )
modPAM = comm . PAMModulator ( M , ' SymbolMapping ' , ' Gray ' , . . . % c o d i f i c a en Gray
' NormalizationMethod ' , ' Average Power ' , . . .
' AveragePower ' , Eavg ) ; % Energia promedio deseada = 1
% Genero un o b j e t o ”demodulador PAM” con l a s mismas e s p e c i f i c a c i o n e s que e l
% modulador
demodPAM = comm . PAMDemodulator ( M , ' SymbolMapping ' , ' Gray ' , . . . % c o d i f i c a en Gray
' NormalizationMethod ' , ' Average Power ' , . . .
' AveragePower ' , Eavg ) ; % Energia promedio deseada
f o r n0 = 1 : l e n g t h ( SNRbdB )
%% Primero t r a b a j o con simbolos y despues a n a l i z o por b i t
sigma = s q r t ( Eavg/SNR ( n0 ) ) ; % desvio de ruido
simbtx = randi ( M , nsimbs , 1 ) −1;
% simbolos a t r a n s m i t i r ( en 1 :M) ;
% l a f u n c i o n ” s t e p ” llama a l o b j e t o modulador o demodulador
simbmod = step ( modPAM , simbtx ) ; % simbolos modulados para su t r a n s m i s i o n ”OJO , son COMPLEJOS”
6
66.78 - Comunicaciones Digitales y Analógicas
Sugerencia para los TPs - Curso Miércoles
% Sumo e l ruido ( OJO sumo e l ruido como s i l a c o n s t e l a c i o n t u v i e r a p a r t e compleja )
simbmod = simbmod + sigma * ( randn ( nsimbs , 1 ) +1i * randn ( nsimbs , 1 ) ) ;
% Demodulo
simbrx= step ( demodPAM , simbmod ) ; % simbolos r e c i b i d o s
% P r o b a b i l i d a d de e r r o r de simbolo simulada
Pes ( n0 ) = nnz ( simbtx ˜= simbrx ) /nsimbs ;
%% Ahora a n a l i z o l o s e r r o r e s de b i t ( e l Gray l o hizo e l modulador )
bitstx = de2bi ( simbtx ) ; % c o n v i e r t o l o s simbolos t r a n s m i t i d o s a b i t s
bitsrx = de2bi ( simbrx ) ; % c o n v i e r t o l o s simbolos r e c i b i d o s a b i t s
% comparo l o s b i t s y cuento cuantos d i f i e r e n
Peb ( n0 ) = nnz ( xor ( bitstx , bitsrx ) ) /k/nsimbs ;
end
%% G r a f i c o s
% P r o b a b i l i d a d de e r r o r de simbolo
figure (1)
semilogy ( SNRbdB , Pet ( SNR ) , '−dr ' , ' l i n e w i d t h ' , 1 . 5 ) ;
hold on
semilogy ( SNRbdB , Pes , '−o ' , ' l i n e w i d t h ' , 1 . 5 ) ;
g r i d on
box on
x l a b e l ( 'SNR por b i t ( dB ) ' ) ;
ylabel ( ' P e ' )
legend ( ' Curva t e o r i c a ' , ' Montecarlo ' )
% P r o b a b i l i d a d de e r r o r por b i t
figure (2)
semilogy ( SNRbdB , Pet ( SNR ) /k , '−dr ' ) ;
hold on
semilogy ( SNRbdB , Peb , '−o ' , ' l i n e w i d t h ' , 1 . 5 ) ;
g r i d on
box on
x l a b e l ( 'SNR por b i t ( dB ) ' ) ;
ylabel ( ' P b ' )
legend ( ' Curva t e o r i c a ' , ' Montecarlo ' )
Observar que como se utilizan pocos valores de SNR frente a la cantidad de promedios que
se hace en cada Montecarlo, se vectoriza el código del Montecarlo para cada valor de SNR y se
utiliza un for para recorrer los valores de SNR deseadas.
Referencias
[1] Feller, William, An Introduction to Probability Theory and its Applications. John Wiley and Sons,
Tercera edición, 1968.
7