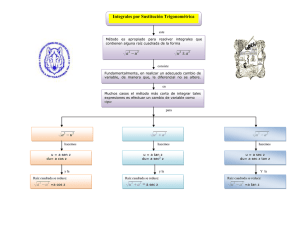
Lectura: Integración trigonométrica

Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
La siguiente lectura tiene por finalidad ser de ayuda para el estudio de la integración de funciones
trigonométricas, esta resume las técnicas de integración usadas cuando parecen potencias enteras
no negativas de funciones trigonométricas o productos particulares de estas potencias, las cuales
han sido desarrolladas en la clase. Además se finaliza con el cambio trigonométrico t = tan( x2 ),
el cual también ha sido desarrollado en clase. Finalmente, se agradece si por algún motivo se
encuentra algún error de cualquier tipo comunicárselo al profesor.
Potencias de senos y cosenos
En este caso, estamos interesados en calcular integrales cuyo integrando son potencias enteras
no negativas de las funciones seno o coseno, es decir de la forma:
Z
Z
n
sen (x) dx o bien,
cosn (x) dx
donde n ∈ Z, n ≥ 0. La técnica a emplear, se basa en decidir como modificar la potencia por
medio del uso de las propiedades de potencias e identidades trigonométricas de tal modo que la
nueva expresión (el integrando) sea más fácil de integrar. Para lograr esto, separamos el problema
en todos los posibles casos que puede asumir n, de la siguiente manera: Para n = 0
sen0 (x) = 1,
por lo que
Z
como también
Z
cos0 (x) = 1
y
0
sen (x) dx =
0
cos (x) dx =
Z
dx = x + C
Z
dx = x + C
Por otro lado, si n = 1, tenemos
Z
Z
1
sen (x) dx = sen(x) dx = − cos(x) + C
mientras que
Z
1
cos (x) dx =
Z
cos(x) dx = sen(x) + C
las cuales son integrales que se encuentran en la tabla. Con esto, hemos mostrado que tanto para
n = 0 y n = 1, las integrales son inmediatas, de esta manera, nos concentraremos en los casos que
n ≥ 2. Entonces, si n ≥ 2 separamos la posible situación en dos casos
(a) Si n es un número impar. En este caso utilizaremos las identidades
sen2 (x) = 1 − cos2 (x),
cos2 (x) = 1 − sen2 (x)
siguiendo la estrategia:
senn (x) = senn−1 (x) sen(x)
= (sen2 (x))
2
n−1
2
sen(x)
= (1 − cos (x))
La Integral Indefinida
n−1
2
sen(x)
1
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
en caso que la potencia sea del seno, y
cosn (x) = cosn−1 (x) cos(x)
= (cos2 (x))
n−1
2
cos(x)
2
= (1 − sen (x))
n−1
2
cos(x)
en caso que la potencia sea del coseno. En ambos casos, desarrollamos el binomio que aparece
como primer factor, seguidamente distribuimos el segundo factor e integramos.
Ejemplo 1. Calcularemos la integral
Z
cos3 (x) dx
Solución: En este caso n = 3, que es un número impar. Ası́
Z
Z
3
cos (x) dx = cos2 (x) cos(x) dx
Z
= (1 − sen2 (x)) cos(x)
Z
= (cos(x) − sen2 (x) cos(x)) dx
Z
Z
= cos(x) dx − sen2 (x) cos(x) dx
de manera que
Z
3
cos (x) dx =
Z
cos(x) dx −
Z
sen2 (x) cos(x) dx
es decir, para obtener el resultado debemos calcular dos integrales que son más fáciles de calcular. En el lado derecho de la igualdad la primera integral es directa, ası́ que nos concentramos
en calcular:
Z
sen2 (x) cos(x) dx
u = sen(x)
Hacemos el cambio
de manera que debemos calcular
du = cos(x) dx
Z
u3
u2 du =
+C
3
y de este modo, regresando el cambio
Z
sen3 (x)
sen2 (x) cos(x) dx =
+C
3
Finalmente, tenemos que
Z
La Integral Indefinida
sen3 (x) dx = sen(x) −
sen3 (x)
+C
3
2
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Ejemplo 2. Calculemos
Z
cos5 (x) dx
Solución: Aquı́ n = 5 que es un número impar. Por lo que, hacemos uso de la misma estrategia
planteada en el ej anterior
Z
Z
5
cos (x) = cos4 (x) cos(x) dx
Z
= (cos2 (x))2 cos(x) dx
Z
= (1 − sen2 (x))2 cos(x) dx
Z
= (1 − 2 sen2 (x) + sen4 (x)) cos(x) dx
Z
= (cos(x) − 2 sen2 (x) + sen4 (x) cos(x)) dx
Z
Z
Z
2
= cos(x) dx − 2 sen (x) cos(x) dx + sen4 (x) cos(x) dx
de manera que
Z
Z
Z
Z
5
2
cos (x) dx = cos(x) dx − 2 sen (x) cos(x) dx + sen4 (x) cos(x) dx
(1)
es decir, para obtener el resultado debemos calcular las tres integrales que aparecen en el lado
derecho de la igualdad (1). La primera es directa, y las otras dos se obtienen por medio de la
sustitución u = sen(x) con lo que du = cos(x) dx, y ası́
Z
u3
u2 du =
+C
3
y
u5
+C
5
por lo tanto, regresando el cambio y sustituyendo en la igualdad se tiene que
3 Z
sen (x)
sen5 (x)
5
cos (x) dx = sen(x) − 2
+
+C
3
5
Z
es decir
Z
u4 du =
cos5 (x) dx = sen(x) −
2
1
sen3 (x) + sen5 (x) + C
3
5
(b) Si n es par, hacemos uso de las identidades del ángulo doble:
sen2 (x) =
La Integral Indefinida
1 − cos(2x)
,
2
cos2 (x) =
1 + cos(2x)
2
3
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
siguiendo el esquema
senn (x) = (sen2 (x)) 2
n
1 − cos(2x) 2
=
2
n
en el caso que la potencia sea del seno, y
cosn (x) = (cos2 (x)) 2
n
1 + cos(2x) 2
=
2
n
en el caso en que la potencia sea del coseno. En ambos casos, desarrollamos el binomio e
integramos.
Ejemplo 3. Calculemos
Z
sen2 (x) dx
Solución. Aquı́ n = 2, que es par. De manera que
Z
Z 1 − cos(2x)
2
sen (x) dx =
dx
2
Z 1 cos(2x)
=
−
dx
2
2
Z
Z
1
cos(2x)
dx −
dx
=
2
2
Z
Z
1
1
=
dx −
cos(2x) dx
2
2
De manera que
Z
1
sen (x) dx =
2
Z
1
dx −
cos(2x) dx
2
R
u = 2x
Para determinar cos(2x) dx hacemos el cambio
y calculamos
du = 2 dx
Z
Z
du
1
1
cos(u)
=
cos(u) du = sen(u) + C
2
2
2
Z
1
1
sen (x) dx = x −
2
2
2
Z
al sustituir, se tendrá
es decir
La Integral Indefinida
2
Z
1
sen(2x) + C
2
1
1
sen2 (x) dx = x − sen(2x) + C
2
4
4
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Ejemplo 4. Calcularemos
Potencias y productos de funciones
trigonométricas
Z
cos4 (x) dx
Solución. Como n = 4 es par, hacemos
Z
Z
4
cos (x) dx = (cos2 (x))2 dx
2
Z 1 + cos(2x)
=
dx
2
Z
(1 + cos(2x))2
dx
=
4
Z
1
=
1 + 2 cos(2x) + cos2 (2x) dx
4
Z
1
1 + cos(4x)
=
1 + 2 cos(2x) +
dx
4
2
Z
1
1 cos(4x)
=
1 + 2 cos(2x) + +
dx
4
2
2
Z
1
3
cos(4x)
=
+ 2 cos(2x) +
dx
4
2
2
1
1 3
x + sen(2x) + sen(4x) + C
=
4 2
8
por lo tanto,
Z
3
1
1
cos4 (x) dx = x + sen(2x) + sen(4x) + C
8
4
8
Productos de potencias de senos y cosenos
Ahora, estamos interesados en calcular integrales de la forma
Z
senn (x) cosm (x) dx
Nuevamente, estudiaremos los posibles casos de ocurrencia para este producto de potencias.
(a) Si m = 1 y n = 1, en este caso el cálculo de la integral se hace por medio de una sustitución
(o cambio de variable) simple, haciendo por ejemplo u = sen(x) entonces du = cos(x) dx y
obtenemos
Z
u2
u du =
+C
2
de manera que, haciendo la correspondiente sustitución, se tiene
Z
sen2 (x)
sen(x) cos(x) dx =
+C
2
La Integral Indefinida
5
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Se debe notar que también es posible hacer el cambio u = cos(x). En este caso debemos tener
cuidado ya que du = − sen(x)dx Es precisamente por este motivo que se adopta de manera
convencional que la sustitución es u = sen(x) en vez de u = cos(x), aunque ambos conducen
a una solución válida.
(b) Si m = 1 y n 6= 1, se tendrá una integral de la forma:
Z
senn (x) cos(x) dx
la cual podemos resolver por haciendo el cambio u = sen(x), du = cos(x) dx, y nos queda
Z
un+1
un du =
+C
n+1
y de este modo,
senn+1 (x)
+C
n+1
Si m 6= 1 y n = 1, se tendrá una integral de la forma:
Z
cosm (x) sen(x) dx
Z
senn (x) cos(x) dx =
De manera análoga, podemos determinar que
Z
cosm+1 (x)
cosm (x) sen(x) dx = −
+C
m+1
(c) Si m es impar. En este caso, expresaremos el producto
senn (x) cosm (x) = senn (x) cosm−1 (x) cos(x)
ahora m − 1 es un número par, luego es divisible por 2 y de esta manera podemos escribir
senn (x) cosm−1 (x) cos(x) = (cos2 (x))
m−1
2
senn (x) cos(x)
por supuesto, conmutando el primer y el segundo factor. Seguidamente, aplicamos la identidad
trigonométrica cos2 (x) = 1 − sen2 (x) para obtener
(cos2 (x))
m−1
2
senn (x) cos(x) = (1 − sen2 (x))
m−1
2
senn (x) cos(x)
para luego desarrollar el binomio que aparece como primer factor y distribuir dos factores
restantes.
Ejemplo 5. Calcularemos
La Integral Indefinida
Z
sen4 (x) cos3 (x) dx
6
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Solución. m = 3 que es impar, por lo que
Z
Z
4
3
sen (x) cos (x) dx = sen4 (x) cos2 (x) cos(x) dx
Z
= (1 − sen2 (x)) sen4 (x) cos(x) dx
Z
= (sen4 (x) cos(x) − sen6 (x) cos(x)) dx
Z
Z
4
= sen (x) cos(x) dx − sen6 (x) cos(x) dx
=
Es decir
Z
sen5 (x) sen7 (x)
−
+C
5
7
sen4 (x) cos3 (x) dx =
sen5 (x) sen7 (x)
−
+C
5
7
En caso que n sea impar, trabajamos de manera análoga.
Ejemplo 6. Calculemos
Z
cos2 (x) sen5 (x) dx
Solución. En este caso n = 5 que es impar. Luego
Z
Z
2
5
cos (x) sen (x) dx = cos2 (x) sen4 (x) sen(x) dx
Z
= (sen2 (x))2 cos2 (x) sen(x) dx
Z
= (1 − cos2 (x))2 cos2 (x) sen(x) dx
Z
= (1 − 2 cos2 (x) + cos4 (x)) cos2 (x) sen(x) dx
Z
= (cos2 (x) sen(x) − 2 cos4 (x) sen(x) + cos6 (x) sen(x)) dx
Z
Z
Z
2
4
= cos (x) sen(x) dx − 2 cos (x) sen(x) dx + cos6 (x) sen(x) dx
de manera que
Z
Z
Z
Z
2
5
2
4
cos (x) sen (x) dx = cos (x) sen(x) dx − 2 cos (x) sen(x) dx + cos6 (x) sen(x) dx
y haciendo los correspondientes cambios de variable, tenemos que
Z
1
2
1
cos2 (x) sen5 (x) dx = − cos3 (x) + cos5 (x) − cos7 (x) + C
3
5
7
La Integral Indefinida
7
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
(d) Si m y n ambos son par, en este caso usaremos las identidades del ángulo doble
sen2 (x) =
1 − cos(2x)
,
2
cos2 (x) =
1 + cos(2x)
,
2
sen(x) cos(x) =
sen(2x)
2
Agrupamos convenientemente y sustituimos.
Ejemplo 7. Calculemos
Z
sen2 (x) cos2 (x) dx
Solución. Usando las identidades trigonométricas se tiene
Z
Z
2
2
sen (x) cos (x) dx = (sen(x) cos(x))2 dx
2
Z sen(2x)
=
dx
2
Z
1
=
sen2 (2x) dx
4
Z
1
1 − cos(4x)
=
dx
4
2
Z
Z
1
1
=
dx −
cos(4x) dx
8
8
1
1
= x−
sen(x) + C
8
32
por lo tanto
Z
1
1
sen(x) + C
sen2 (x) cos2 (x) dx = x −
8
32
Productos de la forma sen(mx) cos(nx).
Aquı́ estamos interesados en calcular las integrales de la forma
Z
Z
Z
sen(mx) cos(nx) dx,
sen(mx) sen(nx) dx
cos(mx) cos(nx) dx
m 6= n
Es decir, productos de senos y cosenos, donde los argumentos son múltiplos constantes distintos
de la variable x. En este caso usamos las identidades:
sen[(m + n)x] + sen[(m − n)x]
2
cos[(m − n)x] − cos[(m + n)x]
sen(mx) sen(nx) =
2
[cos(m − n)x] + cos[(m + n)x]
cos(mx) cos(nx) =
2
sen(mx) cos(nx) =
aquella que sea conveniente en el caso dado.
La Integral Indefinida
8
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Ejemplo 8. Calculemos
Potencias y productos de funciones
trigonométricas
Z
sen(2x) cos(4x) dx
Solución. Haciendo uso de la identidad trigonométrica, con m = 2, n = 4, se tiene
Z
Z
sen[(2 + 4)x] + sen[(2 − 4)x]
dx
sen(2x) cos(4x) dx =
2
Z
Z
sen(6x)
sen(−2x)
=
dx +
dx
2
2
1
1
= − cos(6x) + cos(−2x) + C
12
4
Hay que observar, que en cada caso se usa una de las identidades trigonométricas.
Potencias de tangentes y cotangentes
En esta oportunidad, estamos interesados en calcular integrales de la forma
Z
Z
n
tan (x) dx
cotn (x) dx
para ello usamos
tann (x) = tann−2 (x) tan2 (x)
= tann−2 (x)(sec2 (x) − 1)
= tann−2 (x) sec2 (x) − tann−2 (x)
en caso que la potencia sea de la función tangente. Mientras que
cotn (x) = cotn−2 (x) cot2 (x)
= cotn−2 (x)(csc2 (x) − 1)
= cotn−2 (x) csc2 (x) − cotn−2 (x)
en caso que la potencia sea de la función cotangente. En ambos casos, la integral inicial se puede
escribir como una suma de dos integrales, una de ellas se resuelve cambiando la variable mientras
que la otra es una nueva potencia de la función original reducida en dos unidades, la cual volvemos
a reducir hasta que la integral que resulte por la reducción sea inmediata.
Ejemplo 9. Calculemos
La Integral Indefinida
Z
tan3 (x) dx
9
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Solución.
Z
3
tan (x) dx =
=
Z
Z
tan(x) tan2 (x) dx
tan(x)(sec2 (x) − 1) dx
=
Z
=
tan2 (x)
− ln | cos(x)| + C
2
tan(x) sec2 (x) − tan(x) dx
Z
Z
2
= tan(x) sec (x) dx − tan(x) dx
de manera que
Z
tan3 (x) dx =
Ejemplo 10. Calculemos
Z
tan2 (x)
− ln | cos(x)| + C
2
cot5 (x) dx
Solución.
Z
5
cot (x) dx =
=
Z
Z
cot3 (x) cot2 (x) dx
cot3 (x)(csc2 (x) − 1) dx
Z
cot3 (x) csc2 (x) − cot3 (x) dx
Z
Z
3
= cot (x) csc(x) dx − cot(x) cot2 (x) dx
Z
Z
3
= cot (x) csc(x) dx − cot(x)(csc2 (x) − 1) dx
Z
Z
Z
3
2
= cot (x) csc(x) dx − cot(x) csc (x) dx + cot(x) dx
=
=−
es decir
Z
Ejemplo 11. Calculemos
La Integral Indefinida
cot4 (x) cot2 (x)
+
+ ln | sec(x)| + C
4
2
cot5 (x) dx = −
cot4 (x) cot2 (x)
+
+ ln | sec(x)| + C
4
2
Z
cot4 (x) dx
10
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Solución.
Z
4
cot (x) dx =
=
Z
Z
cot2 (x) cot2 (x) dx
(csc2 (x) − 1) cot2 (x) dx
Z
csc2 (x) cot2 (x) − cot2 (x) dx
Z
Z
2
2
= cot (x) csc (x) dx − (csc2 (x) − 1) dx
Z
Z
Z
2
2
2
= cot (x) csc (x) dx − csc (x) dx + dx
=
=−
cot3 (x)
− ln | csc(x) − cot(x)| + x + C
3
por lo tanto
Z
cot4 (x) dx = −
cot3 (x)
− ln | csc(x) − cot(x)| + x + C
3
Potencias de secantes y cosecantes
Aquı́, calcularemos integrales de la forma
Z
secn (x) dx
Z
cscn (x) dx
en estos casos nuevamente estudiamos los posibles casos que puede asumir n. Si n = 0, n = 1 o
n = 2 las integrales son inmediatas, ya que
sec0 (x) = 1,
de manera que
Z
Z
0
sec (x) dx =
dx = x + C,
o bien
Z
sec1 (x) = sec(x)
Z
sec(x) dx = ln | sec(x) + tan(x)| + C
sec2 (x) dx = tan(x) + C
Cuando la potencia a considerar es de la cosecante, encontramos que también ocurre
Z
Z
Z
0
csc (x) dx =
dx = x + C,
csc(x) dx = ln | csc(x) − cot(x)| + C
o bien
Z
csc2 (x) dx = − cot(x) + C
Por lo tanto, estudiamos que ocurre cuando n > 2, y separamos en dos casos, a saber, si n es par
o bien si n es impar.
La Integral Indefinida
11
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
(a) Si n es par, hacemos una reducción de la potencia en dos unidades y usamos las identidades:
sec2 (x) = 1 + tan2 (x)
csc2 (x) = 1 + cot2 (x)
de la siguiente manera:
secn (x) = secn−2 (x) sec2 (x)
= (sec2 (x))
n−2
2
sec2 (x)
n−2
2
= (1 + tan2 (x))
sec2 (x)
cuando la potencia es de la secante, mientras que
cscn (x) = cscn−2 (x) csc2 (x)
= (csc2 (x))
n−2
2
csc2 (x)
= (1 + cot2 (x))
n−2
2
csc2 (x)
En cualquier caso, desarrollamos el binomio, distribuimos e integramos.
Ejemplo 12. Calculemos
Solución.
Z
6
sec (x) dx =
=
=
=
Z
Z
Z
Z
Z
sec6 (x) dx
sec4 (x) sec2 (x) dx
(sec2 (x))2 sec2 (x) dx
(1 + tan2 (x))2 sec2 (x) dx
(1 + 2 tan2 (x) + tan4 (x)) sec2 (x) dx
Z
(sec2 (x) + 2 tan2 (x) sec2 (x) + tan4 (x) sec2 (x)) dx
Z
Z
Z
2
2
2
= sec (x) dx + 2 tan (x) sec (x) dx + tan4 (x) sec2 (x)) dx
=
= ln | sec(x) + tan(x)| +
Ejemplo 13. Calculemos
La Integral Indefinida
Z
2
1
tan3 (x) + tan4 (x) + C
3
4
csc4 (x) dx
12
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Solución.
Z
4
csc (x) dx =
=
Z
Z
csc2 (x) csc2 (x) dx
(1 + cot2 (x)) csc2 (x) dx
Z
csc2 (x) + cot2 (x) csc2 (x) dx
Z
Z
2
= csc (x) dx + cot2 (x) csc2 (x) dx
=
= − cot(x) −
de manera que
Z
cot3 (x)
+C
3
cot3 (x)
csc (x) dx = − cot(x) −
+C
3
4
(b) Cuando n > 2 y es impar integramos por partes, haciendo
secn (x) = secn−2 (x) sec2 (x)
y de esta manera u = secn−2 (x) y dv = sec2 (x) dx, en caso que la potencia es de la secante.
Análogamente, cuando la potencia es de la cosecante, hacemos
cscn (x) = cscn−2 (x) csc2 (x)
y ası́ hacemos u = cscn−2 (x) y dv = csc2 (x) dx.
Ejemplo 14. Calcularemos
Z
sec3 (x) dx
Solución. En este caso, hacemos


u = sec(x)
du = sec(x) tan(x) dx


dv = sec2 (x) dx v = tan(x)
de este modo
Z
La Integral Indefinida
3
Z
sec(x) sec2 (x) dx
Z
= sec(x) tan(x) − sec(x) tan2 (x) dx
Z
= sec(x) tan(x) − sec(x)(sec2 (x) − 1) dx
Z
= sec(x) tan(x) − sec3 (x) − sec(x) dx
Z
Z
3
= sec(x) tan(x) − sec (x) dx + sec(x) dx
sec (x) dx =
13
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
al despejar tenemos
2
es decir
Z
Z
sec3 (x) dx = sec(x) tan(x) + ln | sec(x) + tan(x)| + C
sec3 (x) dx =
Ejemplo 15. Calcularemos
sec(x) tan(x) + ln | sec(x) + tan(x)|
+C
2
Z
csc3 (x) dx
Solución. En este caso hacemos


u = csc(x)
du = − csc(x) cot(x) dx


2
dv = csc (x) dx v = − cot(x)
de manera que
Z
Z
3
csc (x) dx = − csc(x) cot(x) −
Z
= − csc(x) cot(x) −
Z
= − csc(x) cot(x) −
Z
= − csc(x) cot(x) −
Z
= − csc(x) cot(x) −
csc(x) cot2 (x) dx
csc(x)(csc2 (x) − 1) dx
csc3 (x) − csc(x) dx
Z
3
csc (x) dx + csc(x) dx
csc3 (x) dx + ln | csc(x) − cot(x)| + C
de modo que al despejar, se tiene
Z
2 csc3 (x) dx = − csc(x) cot(x) + ln | csc(x) − cot(x)| + C
una vez más despejamos, y obtenemos
Z
ln | csc(x) − cot(x)| − csc(x) cot(x)
csc3 (x) dx =
+C
2
La Integral Indefinida
14
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Productos de potencias de tangentes con secantes y de cotangentes con cosecantes
En esta ocasión, calcularemos integrales de la forma
Z
Z
n
m
tan (x) sec (x) ó
cotn (x) cscm (x)
Separamos en los posibles casos para n y m.
(a) Caso 1: m es par. En este caso usamos las identidades
sec2 (x) = 1 + tan2 (x)
csc2 (x) = 1 + cot2 (x)
para el correspondiente caso, haciendo la reducción:
tann (x) secm (x) = tann (x) secm−2 (x) sec2 (x)
= tann (x)(sec2 (x))
m−2
2
sec2 (x)
= tann (x)(1 + tan2 (x))
m−2
n
sec2 (x)
o bien,
cotn (x) cscm (x) = cotn (x) cscm−2 (x) csc2 (x)
= cotn (x)(csc2 (x))
m−2
2
= cotn (x)(1 + cot2 (x))
csc2 (x)
m−2
n
csc2 (x)
según sea la integral a resolver. En ambos caso, debemos desarrollar el binomio que aparece,
y distribuir los factores.
Ejemplo 16. Calcularemos
Z
tan4 (x) sec4 (x) dx
Z
tan4 (x) sec2 (x) sec2 (x) dx
Solución.
Z
4
4
tan (x) sec (x) dx =
=
=
Z
Z
tan4 (x)(1 + tan2 (x)) sec2 (x) dx
(tan4 (x) + tan6 (x)) sec2 (x) dx
=
Z
=
tan5 (x) tan7 (x)
+
+C
5
7
tan4 (x) sec2 (x) + tan6 (x) sec2 (x) dx
Z
Z
4
2
= tan (x) sec (x) dx + tan6 (x) sec2 (x) dx
La Integral Indefinida
15
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
de manera que
Z
tan4 (x) sec4 (x) dx =
tan5 (x) tan7 (x)
+
+C
5
7
(b) Caso 2: m y n son impares. En este caso, hacemos uso de las identidades
tan2 (x) = sec2 (x) − 1
cot2 (x) = csc2 (x) − 1
haciendo la reducción
tann (x) secm (x) = tann−1 (x) secn−1 (x) sec(x) tan(x)
= (tan2 (x))
n−1
2
= (sec2 (x) − 1)
secn−1 (x) sec(x) tan(x)
n−1
2
secn−1 (x) sec(x) tan(x)
o bien,
cotn (x) cscm (x) = cotn−1 (x) cscn−1 (x) csc(x) cot(x)
= (tan2 (x))
n−1
2
= (csc2 (x) − 1)
cscn−1 (x) csc(x) cot(x)
n−1
2
cscn−1 (x) csc(x) cot(x)
según sea la integral a resolver. En ambos casos, debemos desarrollar el binomio y distribuir
los factores comunes para luego integrar.
Ejemplo 17. Calcularemos la integral
Z
Solución.
Z
Z
5
3
tan (x) sec (x) dx =
Z
=
Z
=
Z
=
Z
=
Z
=
Z
=
Z
+
La Integral Indefinida
tan5 (x) sec3 (x) dx
tan4 (x) sec2 (x) sec(x) tan(x) dx
(tan2 (x))2 sec2 (x) sec(x) tan(x) dx
(sec2 (x) − 1)2 sec2 (x) sec(x) tan(x) dx
(sec4 (x) − 2 sec2 (x) + 1) sec2 (x) sec(x) tan(x) dx
(sec6 (x) − 2 sec4 (x) + sec2 (x)) sec(x) tan(x) dx
sec6 (x) sec(x) tan(x) − 2 sec4 (x) sec(x) tan(x) + sec2 (x) sec(x) tan(x) dx
Z
6
sec (x) sec(x) tan(x) dx − 2 sec4 (x) sec(x) tan(x) dx
sec2 (x) sec(x) tan(x) dx
16
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
es decir
Z
5
Potencias y productos de funciones
trigonométricas
3
tan (x) sec (x) dx =
+
Z
Z
6
sec (x) sec(x) tan(x) dx − 2
Z
sec4 (x) sec(x) tan(x) dx
sec2 (x) sec(x) tan(x) dx
de manera que nuestra integral estará resuelta si calculamos las tres integrales del lado derecho
de la igualdad. Para tal fin, basta con darse cuenta que haciendo en cada caso el cambio
u = sec(x)
du = sec(x) tan(x) dx
Z
tendremos que para resolver
sec6 (x) sec(x) tan(x) dx, debemos calcular
Z
mientras que, que para resolver
Z
y para resolver
u7
+C
7
sec4 (x) sec(x) tan(x) dx, debemos calcular
Z
Z
u6 du =
u4 du =
u5
+C
5
sec2 (x) sec(x) tan(x) dx debemos calcular
Z
u2 du =
u3
+C
3
de manera que, al sustituir la variable en cada caso, tendremos
Z
1
2
1
tan5 (x) sec3 (x) dx = sec7 (x) − sec5 (x) + sec3 (x) + C
7
5
3
(c) Caso 3: m es impar y n es par. En este caso, hacemos la reducción:
tann (x) secm (x) = (tan2 (x)) 2 secm (x)
n
= (sec2 −1) 2 secm (x)
n
o bien
cotn (x) cscm (x) = (cot2 (x)) 2 cscm (x)
n
= (csc2 −1) 2 cscm (x)
n
según sea la integral que se quiere resolver. En ambos casos, desarrollamos el binomio y distribuimos el factor, para obtener una suma de potencias de la secante o cosecante respectivamente,
las cuales se resuelven como en el apartado anterior.
La Integral Indefinida
17
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
Ejemplo 18. Calcularemos
Z
tan2 (x) sec(x) dx
Solución. Hacemos
Z
2
tan (x) sec(x) dx =
Z
(sec2 (x) − 1) sec(x) dx
Z
sec3 (x) − sec(x) dx
Z
Z
3
= sec (x) dx − sec(x) dx
=
en la primera integral aparece una potencia impar de la secante, por lo que calculamos por
partes. La segunda integral es directa (se encuentra en la tabla).
El cambio t = tan
x
2
Un cambio de variable muy particular es precisamente cuando hacemos
x
t = tan
2
que es utilizado en ocasiones que el integrando es una expresión racional de senos y cosenos.
En general, cuando se tiene una expresión racional de funciones trigonométricas este cambio es
válido, pero es importante destacar que en oportunidades otros cambios, o bien, manipulaciones
algebraicas con identidades trigonométricas, pueden conducir a un resultado correcto y de forma
más sencilla. Este cambio ocurre cuando se hace
x = 2 arctan(t)
al derivar en ambos miembros de la igualdad, se tiene
dx =
2
dt
1 + t2
Por otro lado, ya que
x
x
x
x
sen(x) = sen
+
= 2 sen
cos
2 2
2
2
x
x
sen x2
2
2 x
=2
cos
= 2 tan
cos
2
2
2
cos x2
x
x
tan
tan
= 2 1 2 = 2 2 2x sec 2
cos2 ( x2 )
tan x2
=2
1 + tan2 x2
La Integral Indefinida
18
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
Potencias y productos de funciones
trigonométricas
2 tan x2
y como t = tan
es decir sen(x) =
1 + tan2 x2
x
2
, se tiene
sen(x) =
2t
1 + t2
Mientras que,
x
x
x
= cos2
− sen2
2 2
2!
2
x
2 x
sen 2
2 x
2 x
=
cos
= cos2
1−
1
−
tan
2
2
2
cos2 x2
1 − tan2 x2
1 − tan2 x2
=
=
1
sec2 x2
cos2 ( x2 )
1 − tan2 x2
=
1 + tan2 x2
1 − tan2 x2
por lo que
es decir cos(x) =
1 + tan2 x2
cos(x) = cos
x
+
1 − t2
1 + t2
De esta forma, cuando establecemos que t = tan x2 se tiene que
cos(x) =
sen(x) =
2t
1 + t2
cos(x) =
1 − t2
1 + t2
dx =
2
dt
1 + t2
por lo que, al hacer uso de este cambio, se debe aprender las igualdades anteriores para sustituir
y luego integrar.
Ejemplo 19. Calcularemos
1
dx
1 + sen(x)
Solución. En este caso, al observar la integral, solo debemos hacer uso de las igualdades:
2t
2
sen(x) =
,
dx =
dt
2
1+t
1 + t2
que al sustituir tendremos:
Z
1
2
dt
2t
1 + 1+t2 1 + t2
Z
la cual operamos algebraicamente
Z
Z
1
2
2
dt
=
2 ) dt
2t
1 + 1+t2 1 + t2
(1 + t2 ) + 2t(1+t
2
1+t
Z
Z
1
1
=2
dt = 2
dt
2
1 + t + 2t
(t + 1)2
2
=
+C
t+1
La Integral Indefinida
19
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
por lo que
Potencias y productos de funciones
trigonométricas
Z
2
1
dx =
+C
x
1 + sen(x)
tan 2 + 1
Ejemplo 20. Calcularemos
cos(x)
dx
1 + sen(x)
Solución. En este caso, haciendo t = tan x2 se tiene
Z
cos(x) =
1 − t2
;
1 + t2
sen(x) =
2t
;
1 + t2
dx =
2
dt
1 + t2
al sustituir y operar se tiene
Z
1
1−t2
1+t2
2t
+ 1+t
2
Z
1−t2
2
1+t2
dt = 2
dt
2
1+t
1 + t2 + 2t
Z
1 − t2
dt
=
(1 + t2 )(t2 + 2t + 1)
Z
1 − t2
=
dt
(1 + t2 )(t + 1)2
descomponemos en suma de fracciones simples al integrando
A
B
Cx + D
1 − t2
=
+
+
2
2
2
(1 + t )(t + 1)
t − 1 (t − 1)
1 + t2
A(t + 1)(1 + t2 ) + B(1 + t2 ) + (Cx + D)(t + 1)2
=
(t + 1)2 (1 + t2 )
de esta manera se tiene
1 − t2 = A(t + 1)(1 + t2 ) + B(1 + t2 ) + (Cx + D)(t + 1)2
de manera que al desarrollar el lado derecho de la igualdad se tiene
−t2 + 1 = (A + C) t3 + (A + B + 2 C + D) t2 + (A + C + 2 D) t + (A + B + D)
esta igualdad genera el sistema




el cual al resolver se tiene
A+C
A + B + 2C + D
A + C + 2D



A+B+D
A = 1,
La Integral Indefinida
B = 0,
=
=
=
=
0
−1
0
1
C = −1 D = 0
20
Universidad de Los Andes
Facultad de Ciencias Forestales y Ambientales
Escuela de Ingenierı́a Forestal
Matemáticas II
U-2015
Prof. K. Chang
de manera que
Potencias y productos de funciones
trigonométricas
1
t
1 − t2
=
− 2
2
2
(1 + t )(t + 1)
t+1 t +1
y ası́
Z
1 − t2
dt =
(1 + t2 )(t + 1)2
1
t
− 2
dt
t+1 t +1
Z
Z
1
t
=
dt −
dt
2
t+1
t +1
1
= ln |t + 1| − ln |t2 + 1| + C
2
Z
finalmente, sustituimos los valores de la variable t y obtenemos
Z
1 x
x
cos(x)
dx = ln tan
+ 1 − ln tan2
+1 +C
1 + sen(x)
2
2
2
La Integral Indefinida
21