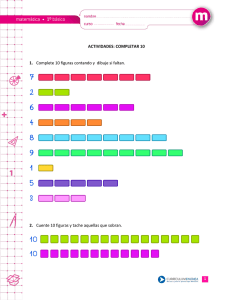
la resta llevándose hasta el número 100

FUNDAMENTOS DEL CÁLCULO ARITMÉTICO
EN EL PRIMER CICLO
DE LA ENSEÑANZA PRIMARIA.
LA RESTA LLEVÁNDOSE
HASTA EL NÚMERO 100
Autor: Ramón Galán González
Introducción.
Una de las preocupaciones que muestra el profesorado en relación a la
enseñanza de las matemáticas en el Ciclo Inicial de la Educación Primaria es la
dificultad para abordar el algoritmo de las llamadas “restas llevándose”. El mismo
profesorado es consciente que el procedimiento empleado para calcular el resultado
numérico en este tipo de operación carece de significación, no solamente para el propio
alumno sino, incluso, para él mismo. Veamos, pues, cual es el algoritmo comúnmente
empleado en las aulas. Pongamos, como ejemplo, la resta 62 – 27.
En primer lugar colocan un número debajo de otro:
62
- 27
Y proceden a continuación diciendo:
-
“De 7 al 12, faltan 5”. (Escriben el 5 debajo de las cifras de las unidades)
“De 12, nos llevamos una”
“2 y 1 que nos llevamos, son 3” (Le suman 1 a la cifra de las decenas del
sustraendo)
“Del 3 para llegar a 6, faltan 3” (Escriben el 3 debajo de las cifras de las
decenas)
Es decir:
62
- 27
3 5
Sin embargo, cuando le preguntamos al profesorado, el motivo por el cual hay
que sumar 1 a la cifra de las decenas del número que figura como sustraendo, se
muestran incapaces de dar una respuesta satisfactoria. Algunos tratan de justificar el
procedimiento diciendo: “Como no podemos quitarle a 2 unidades 7 unidades, entonces
pedimos prestada a la cifra 6, una decena, y de este modo ya tenemos 12”. En este
caso, el profesorado no cae en la cuenta que entonces, y para ser consecuente, en el
procedimiento, tendríamos que restar 1 a las cifras de las decenas del número que
figura como minuendo, en vez de sumar 1 a las cifras de las decenas del número de
abajo. Tal vez, sea en este algoritmo donde se pone de manifiesto con mayor claridad
la falta de significación que tienen, tanto para el alumno como para el profesor, los
procedimientos empleados en el cálculo aritmético. Por ello, dichos algoritmos se
presentan como procedimientos arbitrarios y extraños. Como podremos observar a
continuación, este hecho está motivado por dos razones: Una, por una metodología
inapropiada que desconecta la acción del pensamiento. Dos, por una visión unilateral y
parcial de la operación de restar, al considerarla casi exclusivamente como acción de
quitar, es decir, como acción de descomponer.
A lo largo del presente trabajo, descubriremos el misterio del algoritmo de la
“resta llevándose”, de un modo sencillo y práctico.
C
copyright 2009 Ramón Galán González
2
Fases de la estrategia empleada para la “resta llevándose”
En primer lugar y en relación a la resta llevándose, tenemos que considerarla
siempre como acción de completar y no como acción de quitar o descomponer. Luego,
la estrategia general consistirá en completar el número que figura como sustraendo en
relación a un total representado por el número que figura como minuendo. Es decir,
calcular las que le faltan al sustraendo para llegar al número formado por el minuendo.
Empleando el ejemplo la resta anteriormente mencionada 62 – 27, consistirá en
calcular las que le faltan al número 27 para completar o llegar al número 62.
Como todo proceso, la estrategia que emplearemos para dotar de significación a
la mecanización de la resta llevándose, recorrerá diversas y sucesivas fases. Por ello,
analizaremos a continuación todas y cada una de estas fases propuestas. Para mejor
comprensión de las sucesivas fases y el entrelazamiento de las mismas, tomaremos
como referencia final la mencionada resta 62 – 27.
Las fases de realización de la estrategia empleada para la “resta llevándose
serán:
1ª. Paso de las unidades a la primera decena, empleando objetos representados
y objetos simbólicos sin agrupar. Restas del tipo: 12 – 7
2ª. Paso a la decena siguiente, empleando objetos representados y objetos
simbólicos sin agrupar. Restas del tipo: 32 – 27
3ª. Paso a la decena siguiente, empleando únicamente las regletas. Restas del
tipo: 12 – 7.
4ª. Paso a la decena siguiente, empleando únicamente las regletas. Restas del
tipo: 42 – 37.
5ª. Paso a un número exacto de decenas, empleando únicamente las regletas.
Restas del tipo: 50 – 27.
6ª. Efectuar restas “llevándose” de dos números naturales menores que 100.
Restas del tipo 62 – 27.
C
copyright 2009 Ramón Galán González
3
Fase 1ª. Paso de las unidades a la primera decena, empleando objetos
representados y objetos simbólicos sin agrupar. Restas del tipo: 12 – 7
Comenzamos esta primera fase empleando la “máquina de contar”. Básicamente
consiste en tiras rectangulares de madera fina y poco pesada, cuyas dimensiones son
7 cm. de ancho y 60 cm. de alto. Estas tiras aparecen divididas en 10 partes iguales, es
decir, en 10 rectángulos de 7 cm. de ancho por 6 cm. de alto. En cada uno de estos 10
rectángulos se colocará un trozo de velcro hembra para posibilitar adherir en él los
objetos representados y plastificados. A su vez, las tiras rectangulares, y en su parte
trasera, llevarán colocadas trozos de velcro macho con el fin de adherirla al
franelograma.
Este recurso puede emplearse igualmente para trabajar la construcción del
concepto de número natural formados por dos cifras. En el caso que nos ocupa,
emplearemos este recurso como transición antes de usar las regletas.
Comenzaremos con la siguiente actividad práctica:
Formamos con naranjas el número 12, (una tira completa de 10 naranjas y otra
tira con dos naranjas sueltas) y el número 7 (una tira con 7 naranjas sueltas). Las
pegamos en el franelograma, de este modo:
C
copyright 2009 Ramón Galán González
4
Pegaremos en el franelograma dos personajes: Elena y Javier. Elena será la
chica que tiene las 12 naranjas y Javier será el chico que tiene 7 naranjas. Igualmente
pegaremos en el franelograma varias naranjas. Es decir:
Les preguntaremos a los alumnos:
- ¿Cuántas naranjas tiene Elena? 12.
- ¿Cuántas naranjas tiene Javier? 7
- ¿Quién tiene más naranjas, Elena o Javier? Elena.
- ¿Quién de los dos tiene menos naranjas? Javier.
- ¿Cuántas naranjas tiene que comprar Javier para lograr tener la misma
cantidad que Elena?
Para responder a esta última pregunta, saldrá un alumno y añadirá las naranjas
necesarias para que los dos personajes tengan el mismo número de naranjas. Con tal
fin, trasladará 5 naranjas desde el franelograma hasta las tiras rectangulares con el fin
de completar el número 12. Para ello, completará, en primer lugar, la tira de 7 naranjas
hasta tener 10 y, a continuación, colocará las dos naranjas sueltas. Al mismo tiempo
que las coloca, el alumno tiene que ir contándolas.
5
C copyright 2009 Ramón Galán González
Finalmente, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 7 naranjas hasta llegar a 12 naranjas? 5 naranjas.
El profesor escribirá en la pizarra la operación:
12
–7
5
12 – 7 = 5
Al mismo tiempo que dirá:
- “De 7 a 12 faltan 5”
Se realizarán diversos ejercicios similares variando los números y los objetos
empleados. A la par que se realizan los ejercicios de forma práctica, se realizarán de
forma numérica. Es conveniente, comenzar siendo el sustraendo el número 9, después
C
copyright 2009 Ramón Galán González
6
el 8, el 7, etc. e ir progresivamente aumentando el número que figura como minuendo.
Es decir, restas como las siguientes:
11 – 9 =
12 – 9 =
13 – 9 =
14 – 9 =
etc.
11 – 8 =
12 – 8 =
13 – 8 =
14 – 8 =
etc.
11- 7 =
12 – 7 =
13 – 7 =
14 – 7 =
etc.
Si observamos con detalle el procedimiento empleado, observaremos que el
alumno realiza dos acciones: completar y contar.
Posteriormente, se realizarán ejercicios similares pero empleando objetos
simbólicos independientes. Vemos otro ejemplo con estos nuevos objetos:
Formamos en el franelograma los números 14 y 9.
Formularemos al grupo de alumnos las siguientes preguntas:
-
C
¿Qué número hemos formado en la parte izquierda? (Señalaremos la parte
izquierda con la mano). El 14.
copyright 2009 Ramón Galán González
7
-
¿Qué número hemos formado en la parte derecha? (Señalaremos la parte
derecha con la mano). El 9.
Solicitaremos a dos alumnos que coloquen debajo de cada cantidad las tarjetas
de numeración correspondientes.
Volveremos a preguntar al grupo:
-
¿Cuántos cuadrados, cuántas unidades tendremos que añadir al número 9
para formar también en la parte derecha el número 14? 5
-
Vamos a comprobarlo.
Saldrá un alumno y realizar la acción de completar, desplazando los cinco
cuadrados desde el franelograma a las tiras rectangulares, completando primero la
decena y, posteriormente, añadiendo las 4 unidades. Es decir:
Es conveniente observar dos pequeños detalles:
Uno, que tanto el número 11 como el 6 están presentes de forma perceptiva, de
forma visual y que, por lo tanto, la acción de comparar y de completar contará con la
apoyatura de la percepción visual, quedando reducida, por ello, a que a ambos lados
haya la misma cantidad, haya la misma “imagen”.
C
copyright 2009 Ramón Galán González
8
El segundo detalle es que al comparar visualmente, tendrá que dirigir su mirada
tanto a las decenas como a las unidades y observará que en la tira de las decenas
tiene que añadir 1, puesto que falta una para tenerla completa, mientras que en la tira
de las unidades tendrá que añadir 4 puesto que no tiene ninguna. De este modo,
estamos obligando a los alumnos, mediante la percepción de la cantidad, a
descomponer el número 5 en 1 y 4.
En definitiva y mediante la percepción visual de la cantidad, el alumno irá más
allá de la simple acción de contar para realizar la acción de completar, obligándole, sin
que pueda evitarlo, a realizar la acción de componer.
Finalmente, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 9 hasta llegar a 14? 5
El profesor escribirá en la pizarra la operación:
14
–9
5
14 – 9 = 5
Al mismo tiempo que dirá:
-
“De 9 a 14 faltan 5”
Por último, realizaremos ejercicios similares con las regletas pero colocando en
el franelograma las unidades sueltas que el alumno utilizara para completar el
sustraendo hasta completar el minuendo. Lo vemos con la resta 15 – 8.
Formamos los números en el franelograma:
C
copyright 2009 Ramón Galán González
9
Formularemos al grupo de alumnos las siguientes preguntas:
-
¿Qué número hemos formado en la parte izquierda? (Señalaremos la parte
izquierda con la mano). El 15.
-
¿Qué número hemos formado en la parte derecha? (Señalaremos la parte
derecha con la mano). El 8.
Solicitaremos a dos alumnos que coloquen debajo de cada cantidad las tarjetas
de numeración correspondientes.
Volveremos a preguntar al grupo:
-
¿Cuántas unidades tendremos que añadir al número 8 para formar también
en la parte derecha el número 15? 7
-
Vamos a comprobarlo.
Saldrá un alumno y realizar la acción de completar, añadiendo las 7 unidades
sueltas, completando primero la decena añadiendo 2 unidades y, posteriormente,
añadiendo las 5 unidades sueltas. Es decir:
De nuevo y finalmente, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 8 hasta llegar a 15? 7
El profesor escribirá en la pizarra la operación:
15
–8
7
15 – 8 = 7
Al mismo tiempo que dirá:
C
copyright 2009 Ramón Galán González
10
-
“De 8 a 15 faltan 7”
Para terminar con el análisis de esta fase, indicar que es conveniente que todos
los ejercicios que realicemos de forma práctica en el franelograma, estén reflejados en
el cuaderno de actividades escritas de los alumnos, de forma que cada alumno tendrá
que escribir en su cuaderno el resultado obtenido. El cuaderno de actividades se
adjunta como documento anexo. Cada ejercicio, aparecerá escrito tanto de forma
vertical como horizontal. Es decir, los alumnos tendrán realizar de forma escrita
actividades como las siguientes:
Calcula:
1 1
- 9
C
11 – 9 =
copyright 2009 Ramón Galán González
1 3
- 8
13 – 8 =
11
2ª Fase. Paso a la decena siguiente, empleando objetos representados y objetos
simbólicos sin agrupar. Restas del tipo: 32 – 27
Comenzaremos esta segunda fase realizando ejercicios donde el alumno tenga
que completar la decena situada inmediatamente por encima del número que resta. Por
ejemplo, completar el 27 hasta llegar a 30. Completar la primera decena, hasta el 10,
no se muestra necesario dado que constituye un aprendizaje que el alumno abordó con
anterioridad al trabajar los complementarios del 10. Veamos, para comenzar, la resta
20 – 17.
Procedemos como en la fase anterior, formamos en el franelograma los números
20 y 17. Para ello emplearemos la máquina de contar y los objetos representados, por
ejemplo yogures.
Les preguntaremos a los alumnos:
- ¿Cuántos yogures tiene Elena? 20.
- ¿Cuántos yogures tiene Javier? 17
- ¿Quién tiene más yogures, Elena o Javier? Elena.
C
copyright 2009 Ramón Galán González
12
- ¿Quién de los dos tiene menos yogures? Javier.
- ¿Cuántas yogures tiene que comprar Javier para lograr tener la misma
cantidad que Elena?
Para responder a esta última pregunta, saldrá un alumno y añadirá los yogures
necesarios para que los dos personajes tengan el mismo número de yogures. Con tal
fin, trasladará 3 yogures desde el franelograma hasta las tiras rectangulares con el fin
de completar el número 20. Al mismo tiempo que las coloca, el alumno tiene que ir
contándolas.
Finalmente, el profesor preguntará al grupo:
- ¿Cuántos faltan desde 17 yogures hasta llegar a 20 yogures? 3 yogures.
El profesor escribirá en la pizarra la operación:
20
–17
3
20 – 17 = 3
Al mismo tiempo que dirá:
- “De 17 a 20 faltan 3”
C
copyright 2009 Ramón Galán González
13
Realizaremos ejercicios similares con las regletas pero colocando en el
franelograma las unidades sueltas que el alumno utiliza para completar el sustraendo
hasta completar el minuendo. Veamos la resta. 40 – 34.
Formamos los números en el franelograma:
Formularemos al grupo de alumnos las siguientes preguntas:
-
¿Qué número hemos formado en la parte izquierda? El 40.
-
¿Qué número hemos formado en la parte derecha? El 34.
Solicitaremos a dos alumnos que coloquen debajo de cada cantidad las tarjetas
de numeración correspondientes.
Volveremos a preguntar al grupo:
-
¿Cuántas unidades tendremos que añadir al número 34 para formar también
en la parte derecha el número 40? 6
-
Vamos a comprobarlo.
Saldrá un alumno y realizar la acción de completar, añadiendo las 4 unidades
sueltas. Es decir:
C
copyright 2009 Ramón Galán González
14
De nuevo y finalmente, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 34 hasta llegar a 40? 6
El profesor escribirá en la pizarra la operación:
40
–34
6
40 – 34 = 6
Al mismo tiempo que dirá:
-
“De 34 a 40 faltan 6”
Después de realizar estos cálculos empleando estos recursos materiales,
pasaremos a realizar ejercicios escritos. Es decir, los alumnos tendrán hacer en su
cuaderno, actividades como las siguientes:
Calcula:
2 0
- 1 7
20 – 17 =
3 0
- 2 5
30 – 25 =
He observado, como práctica habitual en las aulas al emplear la metodología
tradicional, que los alumnos cuando realizan este tipo restas, y al aplicar el algoritmo
que han aprendido de forma mecánica y que carece de significación para ellos,
escriben:
2 0
- 1 7
0 3
Este hecho pone de manifiesto que los alumnos no perciben la cantidad o el
número como totalidad, esto es, que operan con cifras y no con cantidades.
Una vez que el alumno ha aprendido a completar la decena situada
inmediatamente por encima del número representado en el sustraendo, abordamos el
aprendizaje del paso a la decena siguiente.
Empezaremos con ejercicios que supongan el paso de la primera a la segunda
decena, es decir, restas del tipo 21 – 18. Para ello, emplearemos los objetos
representados y las tiras de madera de la “máquina de contar”. El procedimiento será el
mismo que el utilizado en los ejercicios anteriores: formaremos los números y
completaremos el sustraendo hasta conseguir tener la misma cantidad de objetos que
representa el número que figura como minuendo. El profesor escribirá en la pizarra,y
C
copyright 2009 Ramón Galán González
15
en forma de lenguaje matemático, la acción que de forma práctica el ha realizado
alumno. Finalmente los alumnos realizarán las correspondientes actividades escritas.
Debemos comenzar con restas donde el minuendo supere en pocas unidades a
la segunda decena y donde al sustraendo le falten pocas unidades para llegar a esta
segunda decena.
Vemos la resta 21 – 18
Formamos los números:
Les preguntaremos a los alumnos:
- ¿Cuántas naranjas tiene Javier? 21.
- ¿Cuántas naranjas tiene Elena? 18
- ¿Quién tiene más naranjas, Elena o Javier? Javier.
- ¿Quién de los dos tiene menos naranjas? Elena.
-
C
¿Cuántas naranjas tiene que comprar Elena para lograr tener la misma
cantidad que Javier? 3.
copyright 2009 Ramón Galán González
16
Para responder a esta última pregunta, saldrá un alumno y añadirá las naranjas
necesarias para que los dos personajes tengan el mismo número de naranjas. Con tal
fin, trasladará 3 naranjas desde el franelograma hasta las tiras rectangulares con el fin
de completar el número 21. Para ello, procuraremos que el alumno complete en primer
lugar la decena incompleta añadiendo dos naranjas y, posteriormente, añada la naranja
suelta. Al mismo tiempo que las coloca, el alumno tiene que ir contándolas. De este
modo:
A continuación, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 18 naranjas hasta llegar a 21 naranjas? 3 naranjas
El profesor escribirá en la pizarra la operación:
21
–18
3
21 – 18 = 3
Al mismo tiempo que dirá:
-
C
“De 18 a 21 faltan 3”
copyright 2009 Ramón Galán González
17
Pasamos directamente al uso de las regletas pero, al igual que en los casos
anteriores, colocando en el franelograma las unidades sueltas que el alumno utiliza
para completar el sustraendo hasta completar el minuendo. Al mismo tiempo, nos
situamos en decenas superiores y vamos aumentando la distancia existente entre el
minuendo y el sustraendo. Veamos, como ejemplo, la resta 44 – 37.
Formamos los números en el franelograma:
Formularemos al grupo de alumnos las correspondientes preguntas:
-
¿Qué número hemos formado en la parte izquierda? El 44.
-
¿Qué número hemos formado en la parte derecha? El 37.
Solicitaremos a dos alumnos que coloquen debajo de cada cantidad las tarjetas
de numeración y volveremos a preguntar al grupo:
-
¿Cuántas unidades tendremos que añadir al número 37 para formar también
en la parte derecha el número 44? 7
-
Vamos a comprobarlo.
Saldrá un alumno y realizar la acción de completar, añadiendo en primer lugar
las 3 unidades hasta formar el número 40 y, posteriormente, colocará las 4 unidades.
Es decir:
C
copyright 2009 Ramón Galán González
18
De nuevo y finalmente, el profesor preguntará al grupo:
- ¿Cuántas faltan desde 37 hasta llegar a 44? 7
El profesor escribirá en la pizarra la operación:
44
–37
7
44 – 37 = 7
Al mismo tiempo que dirá:
-
“De 37 a 44 faltan 7”
Después de realizar estos cálculos empleando estos recursos materiales,
pasaremos a realizar ejercicios escritos. Es decir, los alumnos tendrán hacer en su
cuaderno, actividades como las siguientes:
Calcula:
2 5
- 1 8
C
25 – 18 =
copyright 2009 Ramón Galán González
3 2
- 2 5
32 – 25 =
19
3ª Fase. Paso a la decena siguiente, empleando únicamente las regletas. Restas
del tipo: 12 – 7.
Retornamos, en cierto modo, a la primera fase pero ahora sin emplear unidades
sueltas. Ahora, el alumno se desprenderá de la acción de contar y, por ello, deberá
proceder a dos acciones de completar y a una acción de componer. Estas tres
acciones constituyen la esencia de la resta “llevándose”.
Con el fin de situar en un primer plano las dos acciones de completar,
presentaremos el ejercicio como “un juego” consistente en formar el número
representado en el minuendo, añadiendo únicamente dos regletas al número que figura
como sustraendo. Posteriormente, y con el fin dirigir su pensamiento a la acción de
componer, preguntaremos al alumno sobre la cantidad total que ha añadido.
Vemos el mencionado ejemplo de la resta 12 – 7.
Construimos los números en el franelograma:
Le proponemos a un alumno la actividad, “el juego”:
-
A la izquierda tienes el número 12. A la derecha, el número 7.
-
Tienes que completar el número 7 de la derecha hasta formar otro número
12, pero añadiendo solamente dos regletas.
El alumno cogerá y colocará la regleta 3 para completar el número 10. Después,
cogerá y colocará la regleta 2 para completar el número 12. De este modo:
C
copyright 2009 Ramón Galán González
20
A continuación le preguntaremos al alumno:
-
¿Qué regletas has colocado sobre la regleta 7 para formar el número 10? La
regleta 3.
-
¿Qué regleta has puesto luego para terminar de formar el número 12? La
regleta 2.
-
¿En total, cuantas unidades has tenido que añadir a 7 para formar el número
12? 5 unidades.
-
Por lo tanto, ¿cuántas faltan de 7 para llegar a 12? Faltan 5.
- Ahora vamos a escribir el la pizarra, lo que has hecho:
12
12
Faltan 2
10
Faltan 5
Faltan 3
7
7
- Ahora lo escribimos en forma de resta:
12
–7
5
12 – 7 =
Repetiremos el ejercicio con otros números hasta que los alumnos automaticen
las tres acciones: las dos de completar, más la acción de componer.
Finalmente, realizaremos ejercicios escritos sin contar con la ayuda del
franelograma y ni las regletas. Estos ejercicios se encuentran en el cuaderno de
actividades del alumno. Como ejemplo:
Calcula las que faltan y escribe el resultado de las restas:
11
10
Faltan
1 1
- 8
11 – 8 =
Faltan
8
C
copyright 2009 Ramón Galán González
21
4ª Fase. Paso a la decena siguiente, empleando únicamente las regletas. Restas
del tipo: 42 – 37.
Esta fase es esencialmente igual que la fase anterior puesto que, como
podremos comprobar, el alumno sólo tendrá que operar con las regletas de las
unidades del número que figura como sustraendo.
Construimos los números en el franelograma:
Le proponemos a un alumno la actividad, “el juego”:
-
A la izquierda tienes el número 42. A la derecha, el número 37.
-
Tienes que completar el número 37 de la derecha hasta formar otro número
42, pero añadiendo solamente dos regletas.
El alumno cogerá y colocará la regleta 3 para completar el número 40. Después,
cogerá y colocará la regleta 2 para completar el número 42. De este modo:
A continuación le preguntaremos al alumno:
C
-
¿Qué regletas has colocado sobre la regleta 7 del número 37 para formar el
número 40? La regleta 3.
-
¿Qué regleta has puesto luego para terminar de formar el número 42? La
regleta 2.
copyright 2009 Ramón Galán González
22
-
¿En total, cuantas unidades has tenido que añadir a 37 para formar el
número 42? 5 unidades.
-
Por lo tanto, ¿cuántas faltan de 37 para llegar a 42? Faltan 5.
- Ahora vamos a escribir el la pizarra, lo que has hecho:
42
42
Faltan 2
40
Faltan 5
Faltan 3
37
37
- Ahora lo escribimos en forma de resta:
42
–37
5
42 – 37 =
Repetiremos el ejercicio con otros números hasta que los alumnos automaticen
las tres acciones: las dos de completar, más la acción de componer.
Finalmente, realizaremos ejercicios escritos sin contar con la ayuda del
franelograma y ni las regletas. Estos ejercicios se encuentran en el cuaderno de
actividades del alumno. Como ejemplo:
Calcula
Calcula las que faltan y escribe el resultado de las restas:
21
20
Faltan
2 1
- 1 8
21 – 18 =
Faltan
18
C
copyright 2009 Ramón Galán González
23
5ª Fase. Paso a un número exacto de decenas, empleando únicamente las
regletas. Restas del tipo: 50 – 27.
Es posible que el lector tenga la sensación que está leyendo siempre lo mismo.
Ello es debido a la coherencia interna de la estrategia que proponemos. Esencialmente,
estamos realizando, de forma continua, dos acciones de completar y una acción de
componer pero, y al mismo tiempo, las restas son cada vez más complejas. Es
precisamente esta coherencia interna de la estrategia lo que facilita el aprendizaje que
experimenta el alumno.
En este caso e igualmente, el alumno tendrá que realizar dos acciones de
completar. La primera, para completar la decena incompleta, esto es, hallará el
complementario del 10. La segunda, para completar el número de decenas pero
teniendo en cuenta que, después de la primera acción de completar, tenemos una
decena más. Finalmente, realizará la acción de componer para calcular el número del
resultado final, es decir, juntará, el número de decenas con el número de unidades que
ha tenido que añadir en las dos acciones de completar. Lo vemos con el ejemplo de la
resta 50 – 27.
Construimos los números en el franelograma:
Le proponemos a un alumno la actividad, pero ahora las reglas del “juego” son
un poco diferentes:
-
A la izquierda tienes el número 50. A la derecha, el número 27.
-
Tienes que completar el número 27 de la derecha hasta conseguir tener,
también en la parte derecha, el número 50. Primero tienes que poner la
regleta de las unidades que haga falta, es decir, primero la de color rojo.
Después, las regletas de las decenas que sean necesarias, las regletas de
color azul. Y lo tienes que hacer en este orden.
Evidentemente y desde el punto de vista práctico, podríamos comenzar
colocando las regletas de las decenas. Sin embargo y en este caso, no se
correspondería con la direccionalidad del algoritmo de las resta. Además desde el
punto de vista del movimiento que realiza nuestro pensamiento, partimos desde el
número 27 y completamos primero el número 30, para completar posteriormente el
número 50 tomando como punto de partida el número 30.
C
copyright 2009 Ramón Galán González
24
Cuando el alumno realice la primera acción de completar, le diremos que se
detenga y le formularemos una serie de preguntas. Es decir:
C
-
¿Qué regleta de unidades has colocado? La regleta 3.
-
¿Qué número tenías al principio en la parte derecha? El número 27.
-
¿Qué número tienes ahora en la parte derecha? El número 30.
-
¿Cuándo tenías el número 27, cuántas decenas completa tenías? Dos.
-
¿Ahora, cuando tienes el número 30, cuántas decenas completas tienes? 3
-
¿Por qué tienes ahora tres decenas completas? Porque al colocar la regleta
3 sobre la regleta 7 he formado una nueva decena.
-
Señala en el número 30 que tienes ahora, las dos decenas que tenías al
principio.
-
Señala en el número 30 que tienes ahora, la nueva decena que has formado.
copyright 2009 Ramón Galán González
25
-
Sigue con el ejercicio y termina de completar el número 50 teniendo en
cuenta que ahora tienes el número 30.
-
¿Cuántas decenas has tenido que añadir al número 30 para completar el
número 50? Dos decenas.
-
¿Qué regleta de unidades pusiste antes? La regleta tres.
-
Señala las dos regletas de decenas que has colocado.
-
Señala la regleta de las unidades que pusiste al principio.
-
¿En total qué cantidad has tenido que añadir al número 27 para completar el
número 50? 23
-
¿Cuántas faltan de 27 hasta llegar a 50? 23.
A continuación, el profesor escribirá en la pizarra, de tres formas diferentes, la
resta realizada por el alumno. En primer lugar:
- Ahora vamos a escribir el la pizarra, lo que has hecho:
C
copyright 2009 Ramón Galán González
26
50
50
Faltan 20
30
Faltan 23
Faltan 3
27
27
En segundo lugar, realizaremos la resta verticalmente. Ahora es importante, el
lenguaje que debemos emplear. Escribimos la resta en la pizarra:
5 0
-2 7
-
¿Qué regleta colocamos encima de la regleta 7, para completar el número
10, es decir, para formar una nueva decena? La regleta 3.
-
Entonces, cuando vayamos a restar diremos: de 7 a 10 faltan 3 y formamos
una nueva decena.
Escribiremos la cifra 3 en la columna de las unidades. Es decir
5 0
-2 7
3
A continuación diremos:
-
2 decenas, más una nueva decena que hemos formado, tenemos 3 decenas.
(Si se estima conveniente, escribiremos el número 1, correspondiente a la nueva
decena formada, encima de la cifra 2)
-
De 3 decenas hasta 5 decenas, faltan2 decenas.
Finalmente, escribimos las 2 decenas que faltan:
5 0
-2 7
2 3
C
copyright 2009 Ramón Galán González
27
En tercer lugar, escribiremos en la pizarra la resta colocada horizontalmente.
5 0–27 =
Después de varios ejercicios similares y con el fin de mecanizar el algoritmo, al
mismo tiempo que lo dotamos de significación, un alumno restara los dos números
empleando las dos regletas y el franelograma, otro alumno realiza la misma resta de
forma numérica en la pizarra. El resto del grupo, lo harán en su libreta. Para ello,
propondremos restas que se encuentren en la libreta de actividades numéricas de los
alumnos.
Es importante que tanto el alumno que opera con regletas como el que realiza la
resta numéricamente, vayan “hablando” conforme hacen la resta. Este hecho
favorecerá la correcta mecanización de la resta. Veamos un ejemplo para ilustrar lo que
acabamos de exponer. Veamos la resta 60 – 32
Presentamos el ejercicio tanto en el franelograma como en la pizarra.
6 0
-3 2
Se realiza la primera acción de completar:
C
copyright 2009 Ramón Galán González
28
6 0
-3 2
8
Los alumnos tendrán que decir: “Del 2 hasta llegar a 10, faltan 8. Formamos
una nueva decena.”
Se realiza la acción de completar las decenas que faltan:
6 0
-3 2
2 8
Los alumnos tendrán que decir: “3 decenas, más una nueva decena que
hemos formado, tenemos 4 decenas. De 4 decenas hasta 6 decenas, faltan 2
decenas.”
De igual modo, es conveniente que el alumno que realiza la resta con las
regletas en el franelograma, identifique los tres tipos de decenas: las 3 decenas que
tenía al principio en el número 32, la nueva decena formada y, por último, las 2
decenas que añadió al final.
Después de realizar los suficientes ejercicios empleando las regletas y el
franelograma, pasaremos a prescindir de estos recursos, empleando únicamente los
ejercicios escritos del cuaderno de actividades.
C
copyright 2009 Ramón Galán González
29
6ª Fase. Efectuar restas “llevándose” de dos números naturales menores que
100.
Ahora estamos en condiciones de descubrir definitivamente el misterio del
algoritmo de la resta llevándose. Emplearemos como ejemplo, la resta mencionada al
principio del presente trabajo: 62 – 27.
Construimos los números en el franelograma:
Le proponemos a un alumno la actividad, con las siguientes reglas del “juego” :
-
A la izquierda tienes el número 62. A la derecha, el número 27.
-
Tienes que completar el número 27 de la derecha hasta conseguir tener,
también en la parte derecha, el número 62. Primero, tienes que poner de una
vez todas las regletas rojas que haga falta, es decir, como no las pongas
ahora, en primer lugar, ya no podrás hacerlo después. Luego y en segundo
lugar, las regletas de las decenas que sean necesarias, las regletas de color
azul. Y lo tienes que hacer en este orden.
Cuando el alumno realice la primera acción, colocar las regletas rojas, le diremos
que se detenga y le formularemos una serie de preguntas. Es decir:
C
copyright 2009 Ramón Galán González
30
-
¿Cuántas unidades tenías al principio en la regleta de color rojo del número
27? 7 unidades.
Tapamos las regletas de las decenas del número de la derecha que tenemos
ahora y preguntamos:
-
¿Qué número has formado ahora con las regletas rojas? El 12.
-
¿Qué dos regletas de color rojo has tenido que colocar para formar este
número 12? La regleta 3 y la regleta 2.
-
¿Si al principio tenías 7 y ahora tienes 12, cuántas faltan de 7 para llegar a
12? 5.
Destapamos las regletas de las decenas y seguimos preguntando:
C
-
¿Cuándo decenas completa tenías al principio? Dos.
-
¿Y Ahora, cuántas decenas completas tienes? Tres
-
¿Por qué tienes ahora tres decenas completas? Porque he formado una
nueva decena.
-
Señala, las dos decenas que tenías al principio.
-
Señala la nueva decena que has formado.
-
Sigue con el ejercicio y termina de completar el número 62 teniendo en
cuenta que ya tienes tres decenas completas.
copyright 2009 Ramón Galán González
31
-
¿Cuántas decenas de color azul has tenido que añadir para completar el
número 62? Tres decenas mas.
-
¿En total qué cantidad has tenido que añadir al número 27 para completar el
número 62? 35
-
¿Cuántas faltan de 27 hasta llegar a 62? 35.
El profesor escribirá en la pizarra, tanto de forma vertical como horizontal, el
resultado de la resta sin explicar aún el algoritmo de la operación
6 2
-2 7
3 5
62 – 2 7 = 35
Antes de comenzar con la aplicación del algoritmo de la resta llevándose en su
expresión numérica, deben realizarse suficientes y variados ejercicios prácticos como
el que hemos analizado. Cuando el alumno haya automatizado el procedimiento en su
forma práctica, pasaremos a expresar el procedimiento en forma numérica. Llegado a
este punto, lo realizaremos de la siguiente forma:
Seguimos con nuestro ejemplo de la resta: 62 – 27.
Presentamos el ejercicio tanto en el franelograma como en la pizarra.
6 2
-2 7
C
copyright 2009 Ramón Galán González
32
Se realiza la primera acción: colocar las regletas rojas necesarias:
Decimos: “De 7 unidades hasta 12, faltan 5 y formamos una nueva decena”.
Escribimos:
6 2
-2 7
5
Se realiza la segunda acción: colocar las decenas que faltan:
Decimos: 2 decenas, más una nueva decena, tenemos 3 decenas. De 3
decenas hasta 6 decenas, faltan 3 decenas.”
Escribimos:
C
6 2
-2 7
3 5
copyright 2009 Ramón Galán González
33
De nuevo, es conveniente que el alumno que realiza la resta con las regletas en
el franelograma, identifique los tres tipos de decenas: las 3 decenas que tenía al
principio en el número 27, la nueva decena formada y, por último, las 3 decenas que
añadió al final.
Se muestra conveniente que cuando los alumnos muestren un cierto dominio de
la resta llevándose, se alternen este tipo de resta con ejercicios de restas sin llevarse,
es decir, restas que al efectuar la primera acción de completar no se forma una nueva
decena.
Si bien la resta sin llevarse puede pensarse como acción de quitar o como
acción de completar, en este caso, y con el fin de establecer diferencias entre ambas
restas, las realizaremos como acción de completar.
A modo de ilustración, realizaremos las restas
65 – 38 y 65 – 31.
Comenzamos con la resta llevándose: 65 – 38
Presentamos el ejercicio tanto en el franelograma como en la pizarra.
6 5
-3 8
Se realiza la primera acción: colocar las regletas rojas necesarias:
C
copyright 2009 Ramón Galán González
34
Decimos: “De 8 unidades hasta 15, faltan 7 y formamos una nueva decena”.
Escribimos:
6 5
-3 8
7
Se realiza la segunda acción: colocar las decenas que faltan:
Decimos: 3 decenas, más una nueva decena, tenemos 4 decenas. De 4
decenas hasta 6 decenas, faltan 2 decenas.”
Escribimos:
6 5
-3 8
2 7
Vemos a continuación la resta sin llevar: 65 – 31:
Presentamos el ejercicio tanto en el franelograma como en la pizarra.
6 5
-3 1
C
copyright 2009 Ramón Galán González
35
Se realiza la primera acción: colocar las regletas rojas necesarias:
Decimos: “De 1 unidad hasta 5, faltan 4, pero NO FORMAMOS UNA NUEVA
DECENA”. (Seguimos teniendo 3 decenas)
Escribimos:
6 5
-3 1
4
Se realiza la segunda acción: colocar las decenas que faltan:
Decimos: De 3 decenas hasta 6 decenas, faltan 3 decenas.”
Escribimos:
6 5
-3 1
3 4
Después de realizar los suficientes ejercicios empleando las regletas y el
franelograma, pasaremos a prescindir de estos recursos, empleando únicamente los
ejercicios escritos del cuaderno de actividades.
C
copyright 2009 Ramón Galán González
36
FUNDAMENTOS DEL CÁLCULO ARITMÉTICO
EN EL PRIMER CICLO
DE LA ENSEÑANZA PRIMARIA.
LA RESTA LLEVÁNDOSE
HASTA EL NÚMERO 100.
ANEXO:
CUADERNO DE ACTIVIDADES NUMÉRICAS.
C
copyright 2009 Ramón Galán González
37
Introducción
Los ejercicios numéricos que a continuación se ofertan, se corresponden con
cada una de las fases que acabamos de describir para la estrategia de la resta
llevándose.
Cada actividad está identificada con dos dígitos. El primero hace referencia a la
fase de la estrategia; el segundo dígito, al orden que ocupa la actividad dentro de esa
fase. Por ejemplo, la actividad 3. 4., quiere decir que es la 4ª actividad de la 3ª fase.
Cada alumno trabajará su propio cuaderno de actividades. El profesor, según
tenga organizada la clase, bien podrá entregárselo en su totalidad a cada uno de ellos,
bien entregando una a una las distintas actividades según el trabajo diario y
posteriormente archivándolas.
Es fundamental que antes de realizar las actividades en su fase numérica, se
trabajen de forma práctica mediante el recurso didáctico correspondiente hasta que los
alumnos mecanicen los movimientos y las acciones que llevan implícitas, es decir,
hasta que el pensamiento se anticipe a la acción.
Por último, no es necesario que los alumnos realicen todas las actividades de
cada una de las fases. Y por el contrario, si el profesor lo estima conveniente, pueden
añadirse más actividades para algunas de las fases. Ello dependerá de la facilidad, o la
dificultad, que muestren los alumnos.
C
copyright 2009 Ramón Galán González
38
La resta
llevándose.
llevándose.
Cuaderno de
Actividades
Alumno/a
Alumno a: _______________________________________
C
copyright 2009 Ramón Galán González
39
Alumno/a:
Alumno a:
1. 1.
Calcula:
Calcula:
C
1 1
- 9
11 – 9 =
1 2
- 9
12
12 – 9 =
1 3
- 9
13
13 – 9 =
1 4
- 9
14
14 – 9 =
1 5
- 9
15 – 9 =
1 6
- 9
16
16 – 9 =
1 7
- 9
17 – 9 =
1 8
- 9
18
18 – 9 =
1 1
- 8
11 – 8 =
1 2
- 8
12
12 – 8 =
copyright 2009 Ramón Galán González
40
Alumno/a:
Alumno a:
1. 2.
2.
Calcula:
C
1 3
- 8
13
13 – 8 =
1 4
- 8
14
14 – 8 =
1 5
- 8
15
15 – 8 =
1 6
- 8
16
16 – 8 =
1 7
- 8
17 – 8 =
1 1
- 7
11
11 – 7 =
1 2
- 7
12 – 7 =
1 3
- 7
13
13 – 7 =
1 4
- 7
14 – 7 =
1 5
- 7
15
15 – 7 =
copyright 2009 Ramón Galán González
41
Alumno/a:
Alumno a:
1. 3.
3.
Calcula:
C
1 6
- 7
16
16 – 7 =
1 1
- 6
11
11 – 6 =
1 2
- 6
12
12 – 6 =
1 3
- 6
13
13 – 6 =
1 4
- 6
14 – 6 =
1 5
- 6
15 – 6 =
1 1
- 5
11 – 5 =
1 2
- 5
12
12 – 5 =
1 3
- 5
13 – 5 =
1 4
- 5
14
14 – 5 =
copyright 2009 Ramón Galán González
42
Alumno/a:
Alumno a:
1. 4.
4.
Calcula:
C
1 1
- 4
11
11 – 4 =
1 2
- 4
12
12 – 4 =
1 3
- 4
13
13 – 4 =
1 1
- 3
11
11 – 3 =
1 2
- 3
12 – 3 =
1 1
- 2
11
11 – 2 =
1 4
- 7
14 – 7 =
1 2
- 6
12
12 – 6 =
1 6
- 8
16 – 8 =
1 8
- 9
18
18 – 9 =
copyright 2009 Ramón Galán González
43
Alumno/a:
Alumno a:
2. 1.
1.
Calcula:
C
2 0
- 1 8
20 – 18 =
2 0
- 1 5
20 – 15 =
2 0
- 1 3
20 – 13 =
2 0
- 1 1
20 – 11 =
3 0
- 2 6
30 – 26 =
3 0
- 2 7
30 – 27 =
4 0
- 3 9
40 – 39 =
4 0
- 3 2
40 – 32 =
5 0
- 4 3
50 – 43 =
6 0
- 5 4
60 – 54 =
7 0
- 6 5
70 – 65 =
8 0
- 7 1
80
80 – 71 =
copyright 2009 Ramón Galán González
44
Alumno/a:
Alumno a:
2. 2.
2.
Calcula:
C
2 1
- 1 9
21 – 19 =
2 2
- 1 9
22 – 19 =
2 2
- 1 8
22 – 18 =
2 3
- 1 8
23 – 18 =
2 1
- 1 7
21 – 17 =
2 2
- 1 7
22 – 17 =
2 4
- 1 7
24 – 17 =
2 1
- 1 6
21 – 16 =
2 3
- 1 6
23 – 16 =
2 4
- 1 6
24 – 16 =
2 1
- 1 5
21 – 15 =
2 2
- 1 4
22 – 14 =
copyright 2009 Ramón Galán González
45
Alumno/a:
Alumno a:
2. 3.
3.
Calcula:
C
2 2
- 1 5
22 – 15 =
2 1
- 1 4
2 3
- 1 5
23 – 15 =
2 3
- 1 4
23 – 14 =
2 1
- 1 3
21 – 13 =
2 1
- 1 2
21 – 12 =
2 2
- 1 3
22 – 13 =
2 4
- 1 5
24 – 15 =
2 7
- 1 9
27 – 19 =
2 5
- 1 8
25 – 18 =
2 8
- 1 9
28 – 19 =
2 5
- 1 7
25 – 17 =
copyright 2009 Ramón Galán González
21 – 14 =
46
Alumno/a:
Alumno a:
2. 4.
4.
Calcula:
C
3 1
- 2 9
31 – 29 =
3 2
- 2 9
32 – 29 =
3 2
- 2 8
32 – 28 =
3 3
- 2 8
33 – 28 =
3 1
- 2 7
31 – 27 =
3 2
- 2 7
32 – 27 =
3 4
- 2 7
34 – 27 =
3 1
- 2 6
31 – 26 =
3 3
- 2 6
33 – 26 =
3 4
- 2 6
34 – 26 =
3 1
- 2 5
31 – 25 =
3 2
- 2 4
32 – 24 =
copyright 2009 Ramón Galán González
47
Alumno/a:
Alumno a:
2. 5.
5.
Calcula:
C
3 2
- 2 5
32 – 25 =
3 1
- 2 4
3 3
- 2 5
33 – 25 =
3 3
- 2 4
33 – 24 =
3 1
- 2 3
31 – 23 =
3 1
- 2 2
31 – 22 =
3 2
- 2 3
32 – 23 =
3 4
- 2 5
34 – 25 =
3 7
- 2 9
37 – 29 =
3 5
- 2 8
35 – 28 =
3 8
- 2 9
38 – 29 =
3 5
- 2 7
35 – 27 =
copyright 2009 Ramón Galán González
31 – 24 =
48
Alumno/a:
Alumno a:
2. 6.
6.
Calcula:
C
4 1
- 3 9
41 – 39 =
4 2
- 3 9
42 – 39 =
4 2
- 3 8
42 – 38 =
4 3
- 3 8
43 – 38 =
4 1
- 3 7
41 – 37 =
4 2
- 3 7
42 – 37 =
4 4
- 3 7
44 – 37 =
4 1
- 3 6
41 – 36 =
4 3
- 3 6
43 – 36 =
4 4
- 3 6
44 – 36 =
4 1
- 3 5
41 – 35 =
4 2
- 3 4
42 – 34 =
copyright 2009 Ramón Galán González
49
Alumno/a:
Alumno a:
2. 7.
7.
Calcula:
C
4 2
- 3 5
42 – 35 =
4 1
- 3 4
4 3
- 3 5
43 – 35 =
4 3
- 3 4
43 – 34 =
4 1
- 3 3
41 – 33 =
4 1
- 3 2
41 – 32 =
4 2
- 3 3
42 – 33 =
4 4
- 3 5
44 – 35 =
4 7
- 3 9
47 – 39 =
4 5
- 3 8
45 – 38 =
4 8
- 3 9
48 – 39 =
4 5
- 3 7
45 – 37 =
copyright 2009 Ramón Galán González
41 – 34 =
50
Alumno/a:
Alumno a:
2. 8.
8.
Calcula:
C
5 1
- 4 9
51 – 49 =
6 2
- 5 9
62 – 59 =
7 2
- 6 8
72 – 68 =
8 3
- 7 8
83 – 78 =
9 1
- 8 7
91 – 87 =
5 2
- 4 7
52 – 47 =
6 4
- 5 7
64 – 57 =
7 1
- 6 6
71 – 66 =
8 3
- 7 6
83 – 76 =
9 4
- 8 6
94 – 86 =
5 1
- 4 5
51 – 45 =
6 2
- 5 4
62 – 54 =
copyright 2009 Ramón Galán González
51
Alumno/a:
Alumno a:
2. 9.
9.
Calcula:
C
7 2
- 6 5
72 – 65 =
8 1
- 7 4
9 3
- 8 5
93 – 85 =
5 3
- 4 4
53 – 44 =
6 1
- 5 3
61 – 53 =
7 1
- 6 2
71 – 62 =
8 2
- 7 3
82 – 73 =
8 4
- 7 5
84 – 75 =
9 7
- 8 9
97 – 89 =
9 5
- 8 8
95 – 88 =
8 8
- 7 9
88 – 79 =
8 5
- 7 7
85 – 77 =
copyright 2009 Ramón Galán González
81 – 74 =
52
Alumno/a:
Alumno a:
3. 1.
1.
Calcula las que faltan y escribe el resultado de las restas:
11
10
Faltan
1 1
- 8
11 – 8 =
1 2
- 9
12 – 9 =
1 3
- 9
13 – 9 =
1 3
- 8
13 – 8 =
Faltan
8
12
10
Faltan
Faltan
9
13
10
Faltan
Faltan
9
13
10
Faltan
Faltan
8
C
copyright 2009 Ramón Galán González
53
Alumno/a:
Alumno a:
3. 2.
2.
Calcula las que faltan y escribe el resultado de las restas:
11
10
Faltan
1 1
- 7
11 – 7 =
1 2
- 7
12 – 7 =
1 1
- 6
11 – 6 =
1 5
- 9
15 – 9 =
Faltan
7
12
10
Faltan
Faltan
7
11
10
Faltan
Faltan
6
15
10
Faltan
Faltan
9
C
copyright 2009 Ramón Galán González
54
Alumno/a:
Alumno a:
3. 3.
3.
Calcula las que faltan y escribe el resultado de las restas:
14
10
Faltan
1 4
- 8
14 – 8 =
1 6
- 9
16 – 9 =
1 5
- 8
15 – 8 =
1 3
- 7
13 – 7 =
Faltan
8
16
10
Faltan
Faltan
9
15
10
Faltan
Faltan
8
13
10
Faltan
Faltan
7
C
copyright 2009 Ramón Galán González
55
Alumno/a:
Alumno a:
3. 4.
Calcula las que faltan y escribe el resultado de las restas:
14
10
Faltan
1 4
- 7
14 – 7 =
1 2
- 6
12 – 6 =
1 2
- 5
12 – 5 =
1 3
- 6
13 – 6 =
Faltan
7
12
10
Faltan
Faltan
6
12
10
Faltan
Faltan
5
13
10
Faltan
Faltan
6
C
copyright 2009 Ramón Galán González
56
Alumno/a:
Alumno a:
3. 5.
5.
Calcula
Calcula las que faltan y escribe el resultado de las restas:
11
10
Faltan
1 1
- 5
11 – 5 =
1 3
- 5
13 – 5 =
1 4
- 6
14 – 6 =
1 1
- 4
11 – 4 =
Faltan
5
13
10
Faltan
Faltan
5
14
10
Faltan
Faltan
6
11
10
Faltan
Faltan
4
C
copyright 2009 Ramón Galán González
57
Alumno/a:
Alumno a:
3. 6.
6.
Calcula las que faltan y escribe el resultado de las restas:
15
10
Faltan
1 5
- 7
15 – 7 =
1 7
- 9
17 – 9 =
1 2
- 4
12 – 4 =
1 1
- 3
11 – 3 =
Faltan
7
17
10
Faltan
Faltan
9
12
10
Faltan
Faltan
4
11
10
Faltan
Faltan
3
C
copyright 2009 Ramón Galán González
58
Alumno/a:
Alumno a:
3. 7.
7.
Calcula las que faltan y escribe el resultado de las restas:
17
10
Faltan
1 7
- 8
17 – 8 =
1 1
- 2
11 – 2 =
1 5
- 6
15 – 6 =
1 6
- 8
16 – 8 =
Faltan
8
11
10
Faltan
Faltan
2
15
10
Faltan
Faltan
6
16
10
C
Faltan
Faltan
copyright 2009 Ramón Galán González
59
Alumno/a:
Alumno a:
3. 8.
8.
Calcula las que faltan y escribe el resultado de las restas:
16
10
Faltan
1 6
- 7
16 – 7 =
1 2
- 3
12 – 3 =
1 3
- 4
13 – 4 =
1 4
- 5
14 – 5 =
Faltan
7
12
10
Faltan
Faltan
3
13
10
Faltan
Faltan
4
14
10
Faltan
Faltan
5
C
copyright 2009 Ramón Galán González
60
Alumno/a:
Alumno a:
4. 1.
1.
Calcula las que faltan y escribe el resultado de las restas:
23
20
Faltan
2 3
- 1 8
23 – 18 =
3 3
- 2 8
33 – 28 =
4 3
- 3 8
43 – 38 =
5 3
- 4 8
53 – 48 =
Faltan
Faltan
18
33
30
Faltan
Faltan
28
43
40
Faltan
Faltan
38
53
50
Faltan
Faltan
48
C
copyright 2009 Ramón Galán González
61
Alumno/a:
Alumno a:
4. 2.
2.
Calcula las que faltan y escribe el resultado de las restas:
63
60
Faltan
6 3
- 5 8
63 – 58 =
7 3
- 6 8
73 – 68 =
8 3
- 7 8
83 – 78 =
9 3
- 8 8
93 – 88 =
Faltan
58
73
70
Faltan
Faltan
68
83
80
Faltan
Faltan
78
93
90
Faltan
Faltan
88
C
copyright 2009 Ramón Galán González
62
Alumno/a:
Alumno a:
4. 3.
3.
Calcula las que faltan y escribe el resultado de las restas:
25
20
Faltan
2 5
- 1 9
25 – 19 =
3 1
- 2 8
31 – 28 =
4 2
- 3 7
42 – 37 =
5 1
- 4 6
51 – 46 =
Faltan
19
31
30
Faltan
Faltan
28
42
40
Faltan
Faltan
37
51
50
Faltan
Faltan
46
C
copyright 2009 Ramón Galán González
63
Alumno/a:
Alumno a:
4. 4.
4.
Calcula las que faltan y escribe el resultado de las restas:
65
60
Faltan
6 5
- 5 2
65 – 52 =
7 2
- 6 9
72 – 69 =
8 7
- 7 9
87 – 79 =
9 4
- 8 8
94 – 88 =
Faltan
52
72
70
Faltan
Faltan
69
87
80
Faltan
Faltan
79
94
90
Faltan
Faltan
88
C
copyright 2009 Ramón Galán González
64
Alumno/a:
Alumno a:
4. 5.
5.
Calcula las que faltan y escribe el resultado de las restas:
24
20
Faltan
2 4
- 1 7
24 – 17 =
3 4
- 2 5
34 – 25 =
4 1
- 3 4
41 – 34 =
5 4
- 4 9
54 – 49 =
Faltan
17
34
30
Faltan
Faltan
25
41
40
Faltan
Faltan
34
54
50
Faltan
Faltan
49
C
copyright 2009 Ramón Galán González
65
Alumno/a:
Alumno a:
4. 6.
6.
Calcula las que faltan y escribe el resultado de las restas:
62
60
Faltan
6 2
- 5 8
62 – 58 =
7 3
- 6 7
73 – 67 =
8 1
- 7 9
81 – 79 =
9 1
- 8 7
91 – 87 =
Faltan
58
73
70
Faltan
Faltan
67
81
80
Faltan
Faltan
79
91
90
Faltan
Faltan
87
C
copyright 2009 Ramón Galán González
66
Alumno/a:
Alumno a:
4. 7.
7.
Calcula las que faltan y escribe el resultado de las restas:
25
20
Faltan
2 5
- 1 6
25 – 16 =
3 3
- 2 5
33 – 25 =
4 2
- 3 4
42 – 34 =
5 6
- 4 9
56 – 49 =
Faltan
16
33
30
Faltan
Faltan
25
42
40
Faltan
Faltan
34
56
50
Faltan
Faltan
49
C
copyright 2009 Ramón Galán González
67
Alumno/a:
Alumno a:
4. 8.
8.
Calcula las que faltan y escribe el resultado de las restas:
66
60
Faltan
6 6
- 5 8
66 – 58 =
7 6
- 6 7
76 – 67 =
8 4
- 7 6
84 – 76 =
9 1
- 8 5
91 – 85 =
Faltan
58
76
70
Faltan
Faltan
67
84
80
Faltan
Faltan
76
91
90
Faltan
Faltan
85
C
copyright 2009 Ramón Galán González
68
Alumno/a:
Alumno a:
4. 9.
9.
Calcula las que faltan y escribe el resultado de las restas:
21
20
Faltan
2 1
- 1 2
21 – 12 =
3 2
- 2 3
32
32 – 23 =
4 3
- 3 4
43 – 34 =
5 3
- 4 9
53 – 49 =
Faltan
12
32
30
Faltan
Faltan
23
43
40
Faltan
Faltan
34
53
50
Faltan
Faltan
49
C
copyright 2009 Ramón Galán González
69
Alumno/a:
Alumno a:
4.
4. 10.
10.
Calcula las que faltan y escribe el resultado de las restas:
65
60
Faltan
6 5
- 5 8
65 – 58 =
7 8
- 6 9
78 – 69 =
8 7
- 7 8
87 – 78 =
9 5
- 8 7
95 – 87 =
Faltan
58
78
70
Faltan
Faltan
69
87
80
Faltan
Faltan
78
95
90
Faltan
Faltan
87
C
copyright 2009 Ramón Galán González
70
Alumno/a:
Alumno a:
4.
4. 11.
11.
Calcula las que faltan y escribe el resultado de las restas:
23
20
Faltan
2 3
- 1 6
23 – 16 =
3 1
- 2 3
31 – 23 =
4 5
- 3 7
45 – 37 =
5 3
- 4 7
53 – 47 =
Faltan
16
31
30
Faltan
Faltan
23
45
40
Faltan
Faltan
37
53
50
Faltan
Faltan
47
C
copyright 2009 Ramón Galán González
71
Alumno/a:
Alumno a:
5. 1.
1.
Calcula las que faltan
faltan y escribe el resultado de las restas:
40
20
Faltan
4 0
- 1 9
40 – 19 =
5 0
- 2 8
50 – 28 =
5 0
- 1 7
50 – 17 =
6 0
- 2 6
60 – 26 =
Faltan
19
50
30
Faltan
Faltan
28
50
20
Faltan
Faltan
Faltan
17
60
30
Faltan
Faltan
26
C
copyright 2009 Ramón Galán González
72
Alumno/a:
Alumno a:
5. 2.
2.
Calcula las que faltan y escribe el resultado de las restas:
restas:
80
60
Faltan
8 0
- 5 2
80 – 52 =
7 0
- 2 9
70 – 29 =
8 0
- 2 5
80 – 25 =
9 0
- 6 8
90 – 68 =
Faltan
52
70
30
Faltan
Faltan
29
80
30
Faltan
Faltan
25
90
70
Faltan
Faltan
68
C
copyright 2009 Ramón Galán González
73
Alumno/a:
Alumno a:
5. 3.
3.
Calcula las que faltan y escribe el resultado de las restas:
60
20
Faltan
6 0
- 1 7
60 – 17 =
8 0
- 2 5
80 – 25 =
9 0
- 3 4
90 – 34 =
9 0
- 4 9
90 – 49 =
Faltan
17
80
30
Faltan
Faltan
25
90
40
Faltan
Faltan
34
90
50
Faltan
Faltan
49
C
copyright 2009 Ramón Galán González
74
Alumno/a:
Alumno a:
5. 4.
4.
Calcula las que faltan y escribe el resultado de las restas:
90
60
Faltan
9 0
- 5 8
90 – 58 =
8 0
- 1 7
80 – 17 =
8 0
- 2 9
80 – 29 =
4 0
7
40 – 7 =
Faltan
58
80
20
Faltan
Faltan
17
80
30
Faltan
Faltan
29
40
10
Faltan
Faltan
7
C
copyright 2009 Ramón Galán González
75
Alumno/a:
Alumno a:
5. 5.
5.
Calcula las que faltan y escribe el resultado de las restas:
60
10
Faltan
6 0
6
-
60 – 6 =
4 0
- 2 5
40 – 25 =
8 0
- 3 1
80 – 31 =
9 0
2
90 – 2 =
Faltan
6
40
30
Faltan
Faltan
25
80
40
Faltan
Faltan
31
90
10
Faltan
Faltan
2
C
copyright 2009 Ramón Galán González
76
Alumno/a:
Alumno a:
6. 1.
1.
Resta:
Resta:
2 6
- 1 4
-
3 9
1 6
2 1
- 1 8
3 2
- 1 9
-
4 8
1 5
5 2
- 1 7
6 3
- 1 7
-
7 1
2 4
8 6
- 1 6
9 7
- 1 1
2 2
- 1 5
-
3 5
3 4
-
4 4
1 8
5 2
- 1 5
-
6 8
2 2
-
7 4
2 4
-
8 3
3 4
9 5
- 4 7
3 7
- 1 8
-
4 6
2 0
-
5 9
3 5
6 1
- 5 6
7 2
- 5 9
3 5
- 1 8
C
copyright 2009 Ramón Galán González
77
Alumno/a:
Alumno a:
6. 2.
2.
Resta:
Resta:
-
9 5
1 4
-
5 6
5 4
6 7
- 1 8
-
6 6
5 0
-
2 6
2 5
-
4 6
1 6
C
-
8 8
2 6
7 2
- 3 8
6 5
- 4 9
-
4 8
3 6
3 3
8
2 5
9
-
3 6
2 6
4 1
- 2 3
5 2
- 4 9
-
7 9
6 6
8 1
- 2 9
9 2
- 3 7
-
9 9
1 5
3 1
- 1 2
8 2
- 5 6
-
7 9
3 6
5 1
- 4 3
6 4
7
copyright 2009 Ramón Galán González
78
Alumno/a:
Alumno a:
6. 3.
3.
Resta:
Resta:
-
4 5
2 1
-
9 6
7 1
6 6
- 7
3 6
- 1 4
-
8 3
3 1
-
9 7
2 5
C
-
6 8
2 7
7 1
- 6 3
5 2
- 1 7
-
8 9
5 9
4 1
- 6
3 2
- 3 1
-
7 9
5 6
6 1
- 4 3
4 2
- 3 7
-
5 7
2 6
7 2
- 2 8
9 2
- 3 0
-
6 7
3 7
4 1
- 3 2
2 2
9
-
9 9
3 7
7 1
- 4 3
5 2
- 4 7
copyright 2009 Ramón Galán González
79
Alumno
a:
Alumno/a:
6. 4.
4.
Resta:
Resta:
-
5 2
8
-
7 3
5 6
4 4
- 3 7
8 2
- 1 0
-
5 3
4 1
5 4
- 1 6
4 3
- 7
9 4
- 1 8
-
6 4
2 4
-
5 5
3 6
7 4
- 2 1
7 5
- 5 6
-
6 6
4 4
-
5 5
3 9
9 6
- 8 8
8 7
9
-
8 6
7 4
7 6
- 1 6
3 7
- 2 8
4 8
- 3 9
5 9
- 1 6
5 2
- 1 5
6 3
- 1 8
7 4
1 6
C
copyright 2009 Ramón Galán González
-
80
Alumno/a:
Alumno a:
6. 5.
5.
Resta:
Resta:
8 5
6 1
7 4
6
6 3
- 3 7
7 2
- 2 8
6 1
- 1 5
5 0
- 1 6
6 0
- 4 8
5 3
9
-
4 7
4 4
-
5 3
2 6
4 1
- 3 8
3 5
- 1 7
-
3 4
3 4
4 0
- 1 6
5 7
- 2 1
-
6 3
5 5
-
5 7
3 4
-
4 2
2 7
7 4
- 5 5
6 5
- 1 8
-
5 0
2 4
-
8 9
2 9
7 2
- 2 4
9 3
- 5 7
-
C
copyright 2009 Ramón Galán González
81