deteccion y eliminacion de redundancia de largos segmentos

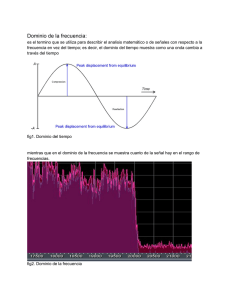
DETECCION Y ELIMINACION DE REDUNDANCIA DE LARGOS
SEGMENTOS EN EL TIEMPO EN SEÑALES DE AUDIO
José R. ZAPATA
Facultad de Telecomunicaciones, Universidad Pontificia Bolivariana
Medellín, Antioquia, Colombia
Ricardo A. GARCÍA
Kurzweil Music Systems
Boston, Massachusetts, USA
RESUMEN
La codificación de audio tradicional esta basada en
compresión perceptual (compresión con pérdidas)
que explota la información psicoacústica para
codificar las señales audio. Este trabajo describe una
nueva técnica para identificar y eliminar segmentos
repetidos de larga duración en una señal audio. El
archivo de audio resultante se comprime mediante
una codificación sin pérdidas. Cuando la señal de
audio es descomprimida y reconstruida se obtiene
una señal casi idéntica a la señal original.
Palabras Clave: Análisis de señales de audio,
Matriz de similitud Compresión de audio sin
pérdidas
1. INTRODUCCION
La compresión de audio sin pérdidas (lossless)
proporciona una copia idéntica o casi igual, bit a bit,
de una señal de audio, luego de un ciclo de
compresión y descompresión. A diferencia de los
algoritmos con pérdidas, los algoritmos sin pérdidas
siempre regeneran la secuencia original de datos, no
importa cuantas veces se realice el proceso de
compresión y descompresión del archivo de audio.
La mayoría de los sistemas de compresión se basan
en análisis de las señales utilizando ventanas cortas
en el tiempo (entre 2 – 50 ms) debido al costo
computacional que conlleva manejar ventanas
mucho más grandes. Pero hacen análisis de
redundancia Inter-canal para aumentar la relación de
compresión. Aunque los codificadores sin pérdida
(lossless) hacen un uso estadístico de la información
redundante y los codificadores con pérdida (lossy)
hacen uso la información perceptualmente
redundante en la música, ninguno de estos tipos de
codificadores hacen uso de las redundancias
estructurales en la música para su codificación, es
decir, que la mayoría de la música se hace a partir
de estructuras repetidas.
La propuesta presentada consiste en analizar un
algoritmo de compresión basado en ventanas de
mayor duración para eliminar la redundancia en
señales de audio monofónicas aprovechando la
estructura musical de las canciones. La hipótesis
principal es que existen archivos de audio en los
cuales la información se repite exactamente en
intervalos largos, debido a que la mayoría de la
música popular (Ej: música electrónica, pop, Rap,
Hip-hop, rock, entre otros) contiene mucho
elementos repetitivos [1]
que pueden tener
duraciones que llegan hasta 30 segundos [2] (Ej. El
coro de una canción).
Este comportamiento es debido a que
frecuentemente, durante las sesiones de grabación
de música popular, se hace uso de la técnica de
copiar y pegar diferentes segmentos de audio para
lograr una canción final (actualmente los artistas
solo graban una vez el coro y este se copia en los
lugares en los que se repite durante la canción).
Esta afirmación es válida para algunos tipos de
música, puesto que, por ejemplo, la música en vivo
o las grabaciones realizadas antes de la era digital,
presentan poca redundancia de este tipo. La
redundancia
de
dichas
grabaciones
es
principalmente del tipo psico-acústico, es decir;
parecen semejantes a la percepción humana. Otro
factor que tiene que ser considerado es que cada tipo
de música es diferente, lo que implica un análisis
particular para cada tipo: dado que la redundancia
que presenta una canción de música electrónica con
el tamaño de los segmentos se determina mediante
Beat tracking [6], luego a los datos de cada
segmento se le calculan las siguientes
características: media, mediana, varianza, cruces por
cero, máximo y mínimo. Con estos datos se
construye la matriz de similitud (figura 2) para cada
característica.
la que presenta una de Jazz o música clásica, es
diferente.
2. INVESTIGACIONES PREVIAS Y
PROPUESTA
Vishweshwara, Rao [3], presenta un método de
compresión basado en la “estructura musical” [4] de
la canción al comparar 4 diferentes características
de la señal de audio: mfcc, chroma, pitch y la escala
de bandas criticas. Con la ayuda de estas
características se determina cuáles segmentos de
audio son similares, mediante la Matriz de Similitud
[5], y se eliminan aquellos que son
significativamente parecidos para obtener la
compresión. de las 4 características que se utilizaron
para determinar la similitud, la que mejor presentó
resultados fue la escala de bandas críticas. Es
importante aclarar que este método solo elimina
segmentos semejantes y no determina la similitud
exacta de los segmentos. Además sufre del
problema del costo computacional ya que todas
estas medidas son en el dominio de la frecuencia.
La matriz de similitud permite obtener los
segmentos redundantes y poder detectar el tamaño y
la posición de la sección redundante que luego se
elimina, y después se almacena el archivo de audio
resultante y la información necesaria para
reconstruir nuevamente el archivo original.
Segmentación
Antes de empezar cualquier proceso con la señal de
audio, ésta debe ser subdividida en segmentos. Cada
segmento se procesa individualmente. Aunque esto
pueda parecer trivial es muy importante en la
detección de la repetición, ya que el tamaño de los
segmentos desempeña un papel crucial. Si el tamaño
de los segmentos es demasiado pequeño entonces la
resolución en el tiempo es muy alta. Pero
desafortunadamente, se aumenta el costo
computacional. Si el tamaño del segmento es
demasiado grande, entonces la resolución del
tiempo sería demasiado grande para extraer la
información exacta. En las investigaciones
anteriores [6] se determina que un tamaño óptimo
para el segmento sería entre 50 milisegundos (2205
muestras) a 100 milisegundos (4410 muestras) de
largo.
Este trabajo describe el funcionamiento general y la
prueba de un algoritmo que permite localizar
eficientemente la redundancia exacta en largos
periodos de tiempo en señales de audio mono-canal,
con patrones repetitivos de larga duración (T > 10
seg) y permite lograr una mejora en la compresión
sin pérdidas (lossless) mediante la eliminación de
estas redundancias de la señal de audio.
3. DETECCION DE REPETICIONES DE
LARGA DURACION
Sería ineficiente experimentar con diversos tamaños
de segmentos para diferentes géneros de música y
diversas canciones, para ver qué tamaño arroja
óptimos resultados. Lo más práctico sería calcular
un tamaño óptimo del segmento para cada canción
Como se puede observar en la siguiente figura, el
algoritmo ADROTA funciona básicamente de la
siguiente manera: Divide la canción en segmentos,
Figura 1. Funcionamiento General del algoritmo
ENTRADA=
WAV (MONOFONICO
44.1 Khz @16 bits)
FILTRADO DE LA MATRIZ
SEGMENTACION POR
MEDIO DE BEAT
TRACKING
DETECCIÓN DEL TAMAÑO
Y LA POSICIÓN DE LA
REDUNDANCIA
EXTRACCIÓN DE
CARACTERÍSTICAS
(MEDIA, MEDIANA,
VARIANZA, CRUCES POR
CERO, MAXIMO Y MINIMO)
ELIMINACIÓN DEL
SEGMENTO REDUNDANTE
CONSTRUCCIÓN DE LA
MATRIZ DE SIMILITUD Y
UMBRAL
SALIDA=
WAV.(SEGMENTADO)
+ INFORMACIÓN DE
RECONSTRUCCIÓN
de forma automática. Con este fin Mildner y Bartsch
y Wakefield [6] sugieren el uso de un tamaño del
segmento que sea múltiplo del golpe (beat) o tiempo
(tempo) de la canción. El razonamiento detrás de
esta teoría es que si la longitud del segmento es
múltiplo del golpe de la canción, la probabilidad de
detectar la similitud entre diversos segmentos
aumentará porque los coros y los versos
comenzarían normalmente “en el golpe (beat)”.
mínimo y el valor máximo, de cada uno de los
segmentos de la canción.
Para encontrar el tamaño del segmento que este
sincronizado con la canción se utiliza un sistema de
detección de golpes (Beat tracking) que calcula el
numero de golpes por minuto (beats per minute,
bpm) en una canción. Un método muy simple y
robusto para extraer el golpe de una canción, si la
canción no contiene tambores fuertes o golpes muy
marcados, es utilizar el algoritmo desarrollado por
Scheirer [7].
Como su nombre lo indica, el propósito de la matriz
de similitud es exhibir las semejanzas entre un
segmento de la canción y todos los otros segmentos.
Mediante la medida de la distancia euclidiana entre
los valores de las características de los segmentos se
puede observar qué tan similares son dos segmentos
de la señal de audio.
Matriz de similitud
El concepto de matriz de similitud, propuesto por
Foote [8], es un método de visualizar la estructura
de la música por su semejanza o desemejanza
acústica en el tiempo, más que las características o
acontecimientos absolutos de la señal de audio.
Figura 2. Matriz de Similitud
Extracción de Características
Luego de que la señal de audio es divida en
segmentos de igual longitud, a cada uno de estos
segmentos se le calculan diferentes características.
Como se había mencionado anteriormente, las
investigaciones previas se habían concentrado en
encontrar segmentos parecidos (medida subjetiva) y
para esto se había utilizado diferentes medidas,
como la frecuencia fundamental, MFCC (melfrequency cepstral coefficients), Chroma, y la escala
de bandas criticas (Critical Band Scale Rate), siendo
esta ultima la mejor solución.El principal problema
de estas medidas es que se necesita mucha
capacidad computacional para realizar el cálculo de
cada una de ellas, además de la capacidad de
memoria que se utiliza en cada uno de los procesos.
En este trabajo se busca encontrar redundancias
exactas (bit a bit), por lo que se realizaron pruebas
con otro tipo de características que fueran más
objetivas y
que cumplieran las siguientes
condiciones:
•
El costo computacional requerido para su
cálculo debe ser bajo para aumentar la velocidad de
la detección
•
Los datos de las características deben ser
pocos y ocupar poca memoria, para no comprometer
el rendimiento en memoria del procesador al
calcular las diferentes características.
Las características que se escogieron para las
pruebas fueron: la media aritmética, la mediana, la
varianza, el número de cruces por cero el valor
Si los segmentos tienen un alto grado de similitud,
estos serán visibles como líneas diagonales paralelas
a la diagonal principal, esto es porque los segmentos
similares generalmente ocurren en sucesión, y
forman segmentos mas largos similares (p.e. un coro
repetido), siendo la distancia entre estas el tiempo
en que se repite, y la longitud de la línea la duración
aproximada de la redundancia.
Luego de obtener la matriz de similitud y obtener
los valores mas significativos se obtiene una matriz
como se muestra en la figura 2. Como se puede
observar, la matriz tiene muchos datos (vistos como
puntos distribuidos por la matriz) que no se
necesitan y agregan más complejidad a la búsqueda
de las diagonales. Para reducir esto se filtra la matriz
puede encontrar la posición exacta del inicio en el
cual segmento repetido es exacto al segmento
original.
con un filtro pasa bajos mediante una convolución
en dos dimensiones de la matriz de similitud con
una función de gaussiana diagonal debido a que solo
se quiere identificar diagonales, la grafica del kernel
se puede apreciar a continuación.
Eliminación del segmento Redundante
Luego de la detección del segmento repetido en la
señal de audio, se procede a eliminarlo y a guardar
los datos que permitan reconstruir la canción
exactamente después de este proceso. Los datos a
almacenar son el tiempo del inicio y de finalización
del segmento que se repite, y el tiempo en el que se
repite el segmento en la canción.
Figura 3. Kernel Diagonal Gaussiano
-3
x 10
1.5
1
0
0.5
Luego de este proceso de eliminación del segmento
redundante se procede a hacer una codificación sin
pérdidas de la canción, de esta forma disminuir el
tamaño de la canción para ser almacenada.
10
4. RESULTADOS Y COMPARACIONES
20
0
0
5
10
15
30
20
25
30
40
35
Detección de la repetición
De la matriz de similitud filtrada se extraen las
diagonales (recordar que la matriz es simétrica), que
representan la presencia de un segmento redundante.
Con la posición del inicio de la diagonal se puede
obtener la información aproximada del inicio de la
redundancia y según la longitud de ésta se puede
obtener una aproximación de la longitud de la
redundancia.
Para determinar el inicio exacto de la redundancia,
se hace una correlación cruzada entre las muestras
del segmento original y el repetido, la longitud del
segmento se obtiene con la longitud de la diagonal,
al hacer la correlación se obtiene el punto exacto en
el cual los dos segmentos son mas parecidos,. Dado
que se busca una similitud exacta, se busca el punto
donde la correlación es igual a uno y con ese dato se
El algoritmo ADROTA esta compuesto por una
parte de detección y eliminación de redundancias
largas y otra parte que esta conformada por un
codificador de audio sin pérdidas predictivo. El
desempeño del algoritmo fue evaluado mediante
pruebas controladas codificando 5 archivos de audio
que fueron seleccionados y modificados para que
cumplieran con las siguientes especificaciones:
longitud promedio de un minuto y medio con
existencia de segmentos exactamente redundantes
de mínimo 10 segundos. Todas las señales de audio
son monofónicas, muestreadas a 44.1 Khz. con 16
bits de cuantización.
El desempeño del algoritmo se calculo mediante el
factor de compresión, r que equivale a la relación
de compresión
r = 100% −
Tamaño resultado
Tamaño original
× 100
Tabla 4. Resultados de compresión de Monkey's, Optimfrog, LA, TTA y FLAC
Original
(MB)
Comprimida (MB)
Monkey's Audio
.APE
MB
R%
OptimFrog
MB
R%
LA
MB
TTA .TTA
R%
FLAC .FLAC
MB
R%
MB
R%
Pista 1
9,57
5,94
37,93%
6,03
36,99%
6,17
35,53%
6,21
35,11%
6,34
33,75%
Pista 2
10,295
6,36
38,22%
6,46
37,25%
6,6
35,89%
6,7
34,92%
6,83
33,66%
Pista 3
10,721
7,14
33,40%
7,24
32,47%
7,39
31,07%
7,53
29,76%
7,64
28,74%
Pista 4
11,67
7,755
33,55%
7,671
34,27%
7,548
35,32%
7,856
32,68%
8,1
30,59%
Pista 5
9,575
6,229
34,95%
6,215
35,09%
6,1
36,29%
6,336
33,83%
6,771
29,28%
Tabla 5. Resultados de compresión de Monkey's, Optimfrog, LA, TTA y FLAC
Original
(MB)
Comprimida (MB)
SHORTEN .SHT
ADROTA + FLAC
.FLAC
ADROTA .JRZ
WINRAR .RAR
WINZIP .ZIP
MB
R%
MB
R%
MB
R%
MB
R%
MB
R%
Pista 1
9,57
6,63
30,72%
4,626
51,66%
4,449
53,51%
6,71
29,89%
9,04
5,54%
Pista 2
10,295
7,16
30,45%
5,543
46,16%
5,307
48,45%
7,218
29,89%
9,766
5,14%
Pista 3
10,721
7,87
26,59%
6,3
41,24%
6,029
43,76%
7,934
26,00%
10,4
2,99%
Pista 4
11,67
8,371
28,27%
7,423
36,39%
7,15
38,73%
8,43
27,76%
10,85
7,03%
Pista 5
9,575
6,714
29,88%
4,643
51,51%
4,5
53,00%
6,82
28,77%
9
6,01%
Figura 4. Resultados de compresión de Monkey's, Optimfrog, LA, TTA y FLAC
Porcentaje promedio de compresion
50,00%
45,00%
40,00%
35,00%
30,00%
25,00%
20,00%
15,00%
10,00%
5,00%
ZI
P
IN
W
RA
R
IN
+
TA
AD
R
O
W
FL
AC
O
TA
AD
R
TE
N
R
O
A
TT
LA
FL
AC
SH
M
on
k
ey
O
pt
im
Fr
og
0,00%
5. ANALISIS DE RESULTADOS
Los resultados de compresión obtenidos en las
pruebas controladas se obtuvo una mejora en
promedio de 9,78% en la compresión con tiempos
de codificación más elevados debido a la
implementación realizada en Matlab, utilizando solo
ADROTA. Utilizando la detección de redundancia
de ADROTA y la compresión de FLAC, se obtuvo
una mejora promedio en la compresión de 11,88%.
Todo esto con respecto a los codificadores
analizados: FLAC, TTA, OptimFROG, LA,
SHORTEN y Monkey’s Audio.
Comparando el desempeño que se logra con las
diferentes características de la señal, las medidas de
máximo y mínimo del segmento fueron los que
presentaron los mejores resultados, ya que permitían
encontrar las diagonales de repetición en la matriz
de similitud. Visualmente con las otras medidas
(media, mediana, varianza y cruces por cero) se
pueden observar las similitudes, pero el rango de
similitud es pequeño, y hace difícil discriminar
cuando dos segmentos son iguales.
En futuros trabajos se puede analizar la redundancia
en intervalos de tiempo entre 250 mseg y 10 seg, y
las redundancias que se presentan adyacentemente,
ya que la matriz de similitud no permite identificar
precisamente cuando ocurren estos eventos.
6. CONLUSIONES
La gran mayoría de los codificadores sin pérdidas
(“lossless”) utilizan métodos de modelación por
predicción. Los codificadores más populares y que
presentan mejor desempeño, en velocidad y razones
de compresión, son: FLAC, TTA, OptimFROG, LA,
SHORTEN y Monkey’s Audio. Algunos
codificadores, como ALAC, Windows Media Audio
Lossless y RealAudio Lossless, entre otros, no
tienen disponible archivos ejecutables, por lo tanto
no se pudieron hacer pruebas de desempeño con
ellos.
Según las pruebas y las investigaciones que se
realizaron, se determinó que los codificadores
“lossless” existentes no tienen en cuenta las
redundancias en largos periodos de tiempo.
El proceso que se realiza de búsqueda y eliminación
de redundancias de larga duración es independiente
y transparente a la posterior codificación. Por esto
puede ser implementado tanto para codificaciones
sin pérdidas (lossless) como en codificaciones con
pérdidas (Lossy).
Las medidas del máximo y el mínimo de los
segmentos permiten encontrar con un bajo costo
computacional repeticiones exactas en las señales de
audio, pero no son buenas medidas para determinar
segmentos parecidos, para esto es mejor utilizar
características en la frecuencia como se vio en los
trabajos analizados en el estado del arte.
Se puede mejorar el algoritmo de búsqueda de
redundancias si se pueden determinar redundancias
de aproximadamente 1 segundo de duración y que
sean consecutivos, por ejemplo en la denominada
música electrónica.
Si la canción que se desea comprimir no tienen
ningún elemento redundante es mejor utilizar los
codificadores actualmente existentes ya que
ADROTA computacionalmente es demorado y no
agrega ningún valor agregado, por esto las mejores
aplicaciones en las que se puede aplicar ADROTA
es en las disqueras en el proceso de grabación, antes
de la masterización, en canciones repetitivas como
en la música electrónica, en canciones generadas por
sintetizadores MIDI, etc.
7. REFERENCIAS
[1] AUCOUTURIER,
Jean-Julien.
Finding
repeating patterns in acoustic musical signals:
applications for audio thumbnailing, AES 22
International Conference on Virtual, Synthetic
and Entertainment Audio, 2002.
[2] CHAI Wei, Barry Vercoe, Structural analysis of
musical signals for indexing and thumbnailing,
Proceedings of ACM/IEEE Joint Conference on
Digital Libraries, 2003.
[3] RAO, Vishweshwara. Audio compression using
repetitive structures in music, florida, EEUU.
Mayo 2004.
[4] DANNENBERG R. & Hu N., “Pattern
discovery techniques for music audio” ISMIR
Conference proceedings: Third international
conference on music information retrieval, pp.
63-70, 2002.
[5] COOPER M. & Foote J., “Summarizing popular
music via structural similarity analysis”, IEEE
workshop on applications of signal processing
to audio and acoustics, New Paltz, New York,
pp. 127-130, Oct 19-22, 2003.
[6] MILDNER V., Klenner P. & Kammeyer K.,
“Chorus detection in songs of pop
music”,Elektronische Sprachsignalverabeitung
(ESSV 2003), Karlsruhe, Germany, September,
24th-26th 2003. Poli, A. Picialli, S. T. Pope, and
C. Roads Eds. Swets & Zeitlinger, Lisse,
Switzerland, 1996.
[7] SCHEIRER E., “Tempo and beat analysis of
acoustic musical signals.” Journal of the
Acoustical Society of America, vol.103, no. 1,
pp. 588-601, 1998.
[8] FOOTE J., "Automatic audio segmentation
using a measure of audio novelty." Proc. Of
IEEE International Conference on Multimedia
and Expo, vol. I, pp. 452-455, 2000.