Análisis comparativo de modelos tridimensionales

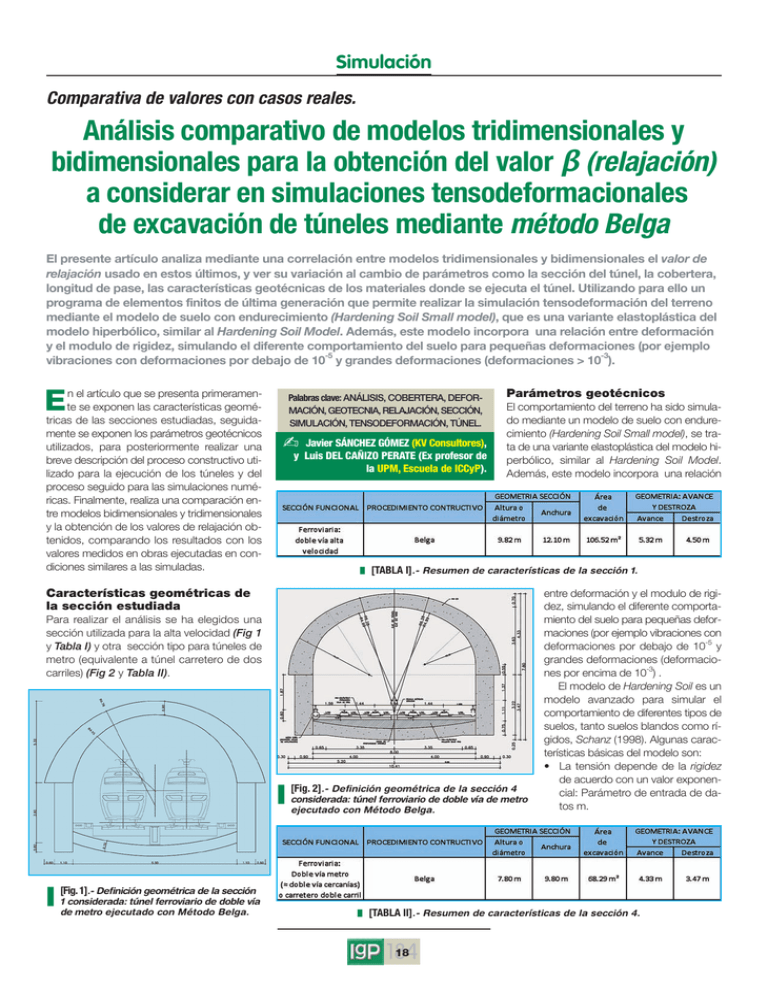
Simulación
Comparativa de valores con casos reales.
Análisis comparativo de modelos tridimensionales y
bidimensionales para la obtención del valor β (relajación)
a considerar en simulaciones tensodeformacionales
de excavación de túneles mediante método Belga
El presente artículo analiza mediante una correlación entre modelos tridimensionales y bidimensionales el valor de
relajación usado en estos últimos, y ver su variación al cambio de parámetros como la sección del túnel, la cobertera,
longitud de pase, las características geotécnicas de los materiales donde se ejecuta el túnel. Utilizando para ello un
programa de elementos finitos de última generación que permite realizar la simulación tensodeformación del terreno
mediante el modelo de suelo con endurecimiento (Hardening Soil Small model), que es una variante elastoplástica del
modelo hiperbólico, similar al Hardening Soil Model. Además, este modelo incorpora una relación entre deformación
y el modulo de rigidez, simulando el diferente comportamiento del suelo para pequeñas deformaciones (por ejemplo
vibraciones con deformaciones por debajo de 10-5 y grandes deformaciones (deformaciones > 10-3).
n el artículo que se presenta primeramente se exponen las características geométricas de las secciones estudiadas, seguidamente se exponen los parámetros geotécnicos
utilizados, para posteriormente realizar una
breve descripción del proceso constructivo utilizado para la ejecución de los túneles y del
proceso seguido para las simulaciones numéricas. Finalmente, realiza una comparación entre modelos bidimensionales y tridimensionales
y la obtención de los valores de relajación obtenidos, comparando los resultados con los
valores medidos en obras ejecutadas en condiciones similares a las simuladas.
E
Palabras clave: ANÁLISIS, COBERTERA, DEFORMACIÓN, GEOTECNIA, RELAJACIÓN, SECCIÓN,
SIMULACIÓN, TENSODEFORMACIÓN, TÚNEL.
Javier SÁNCHEZ GÓMEZ (KV Consultores),
y Luis DEL CAÑIZO PERATE (Ex profesor de
la UPM, Escuela de ICCyP).
Parámetros geotécnicos
El comportamiento del terreno ha sido simulado mediante un modelo de suelo con endurecimiento (Hardening Soil Small model), se trata de una variante elastoplástica del modelo hiperbólico, similar al Hardening Soil Model.
Además, este modelo incorpora una relación
䡵 [TABLA I].- Resumen de características de la sección 1.
Características geométricas de
la sección estudiada
Para realizar el análisis se ha elegidos una
sección utilizada para la alta velocidad (Fig 1
y Tabla I) y otra sección tipo para túneles de
metro (equivalente a túnel carretero de dos
carriles) (Fig 2 y Tabla II).
䡵 [Fig. 2]
.- Definición geométrica de la sección 4
considerada: túnel ferroviario de doble vía de metro
ejecutado con Método Belga.
䡵 [Fig. 1]
.- Definición geométrica de la sección
1 considerada: túnel ferroviario de doble vía
de metro ejecutado con Método Belga.
entre deformación y el modulo de rigidez, simulando el diferente comportamiento del suelo para pequeñas deformaciones (por ejemplo vibraciones con
-5
deformaciones por debajo de 10 y
grandes deformaciones (deformacio-3
nes por encima de 10 ) .
El modelo de Hardening Soil es un
modelo avanzado para simular el
comportamiento de diferentes tipos de
suelos, tanto suelos blandos como rígidos, Schanz (1998). Algunas características básicas del modelo son:
• La tensión depende de la rigidez
de acuerdo con un valor exponencial: Parámetro de entrada de datos m.
䡵 [TABLA II].- Resumen de características de la sección 4.
18
184
Simulación
䡵 [TABLA III]
.Parámetros
del modelo
Hardening
Soil en
Plaxis.
• Deformación plástica debida a la primera
tensión desviadora: Parámetro de entrada de datos Eref50 .
• Deformación plástica debida a la primera
compresión: Parámetro de entrada de
datos Eref oed .
• Descarga y recarga elástica: Parámetro
de entrada de datos Eref ur , uur
• Criterio de rotura de acuerdo con el modelo de Mohr-Coulomb: Parámetros c, Φ
yψ.
El modelo de Hardening Soil implica un total de once parámetros que quedan sintetizados y agrupados en la Tabla III (algunos parámetros del presente modelo de Hardening Soil
coinciden con aquellos del modelo de MohrCoulomb. Estos son los parámetros de rotura
c, Φ y ψ .)
El modelo original de Hardening Soil asume
un comportamiento elástico del material durante descarga y recarga. Sin embargo, el rango de deformaciones en el cual los suelos
pueden ser considerados verdaderamente
elásticos es muy pequeño. Cuando se producen incrementos en las deformaciones, la rigidez del suelo decae no-linealmente. Representando la rigidez del suelo con respecto a
log(deformación), se genera una curva en forma de S en la que se produce una disminución de la rigidez. La Fig. 3 ofrece un ejemplo
de este tipo de curva de reducción de la rigidez. Esto subraya además que la deformación
característica de cortante puede ser medida
cerca de estructuras geotécnicas o aplicar los
rangos de deformación obtenidos de los ensayos de laboratorio.
䡵 [Fig. 3]
cas pertenecientes al Pliocuaternario. Para realizar la citada caracterización se ha recogido
la información geotécnica recogida en los siguientes proyectos:
• Proyecto de construcción de plataforma. LAV. Madrid-Zaragoza-BarcelonaFrontera Francesa. Tramo La TorrassaSants (Tabla IV).
䡵 [TABLA IV]
.- Parámetros del modelo con endurecimiento considerando la diferente
rigidez del suelo con pequeñas deformaciones (hardening Soil with Small Strain).
De esto resulta que con la mínima deformación, la cual se puede medir formalmente
mediante ensayos clásicos de laboratorio, por
ejemplo, ensayos triaxiales y ensayos edométricos sin instrumentación especial, la rigidez
del suelo disminuye generalmente a menos de
la mitad de su valor inicial.
La rigidez de un suelo que debe ser empleada en el análisis de estructuras geotécnicas
no es la que se relaciona con el rango de deformación al final de la construcción, de
acuerdo con la Figura 3.
En cambio, las rigideces para deformaciones muy pequeñas y su dependencia no lineal
con las deformaciones deben ser correctamente tenidos en cuenta.
Además, de todos los aspectos del modelo de Hardening Soil, el modelo HSsmall ofrece
la posibilidad de hacerlo.
El modelo HSsmall, implantado en Plaxis,
está basado en el modelo Hardening Soil y
emplea casi completamente los mismos parámetros. De hecho, sólo se necesitan dos parámetros adicionales para describir el comportamiento de la rigidez para pequeñas deformaciones:
• El módulo de cizallamiento inicial o para
deformaciones muy pequeñas G0.
• El valor de la deformación de cortante
γ0.7 para el cual el módulo secante
de cizallamiento Gs se reduce a un
valor en torno al 70% de G0.
.- Comportamiento rigidez característicadeformación de un suelo con el rango típico de
deformaciones de ensayos de laboratorio y estructuras
(según Atkinson y Sallfors, 1991).
Para la ejecución de los cálculos
se han definido dos perfiles de cálculo cuyos terrenos se corresponden con alguno de los atravesados
por los túneles que se utilizarán para
la comprobación de los resultados
obtenidos en los cálculos.
Los perfiles estratigráficos están
formados por unidades litológicas
que corresponden al área de Barcelona, concretamente a la zona de
estación de Sants que se corresponden a distintas unidades litológi19
184
Proceso constructivo utilizado.
Método Belga
El método Belga es un sistema constructivo
de túneles con entibación integral para terrenos blandos -suelos- de baja estabilidad, los
cuales no permiten mantener áreas desguarnecidas después de excavadas. El método en
resumen consiste en la excavación de la parte alta de la bóveda en pequeños tramos,
avance, como primera fase y posterior excavación de la destroza central, hastiales y contrabóveda.
El proceso consta de varias fases que se
van realizando sucesivamente, construyendo
primeramente la media sección superior y posteriormente el resto. Las fases son:
1. Sección de avance. Bóveda.- La excavación comienza por la galería central de avance o mina. Una vez ejecutada la galería de
avance se efectúan las sucesivas fases de ensanche lateral, concluyendo con los apoyos
extremos de la bóveda. Toda la excavación del
avance se realiza manualmente. Inmediatamente después de ejecutada la excavación se
procede al encofrado y hormigonado de la
sección de bóveda
2. Destroza central.- Una vez hormigonada la bóveda y con un desfase de unos 5 ó 6
anillos, se comienza la destroza, consistente
en excavar una caja central dejando un resguardo del orden de 1 a 1,50 m en los hastiales, para que los empujes que la bóveda transmita al terreno que sirve de apoyo no formen
planos de rotura peligrosos, que pudieran dar
origen a asentamientos y rotura de la misma.
3. Hastiales.- Finalizada la destroza, se
ejecutarán los hastiales por bataches al tresbolillo. Cada batache abarca dos semianillos,
al objeto de no descalzar ningún anillo de la
misma.
4. Solera o contrabóveda.- Se realiza la
excavación correspondiente con máquina, en
una longitud de 10-15 m (5 anillos). Se hormigona posteriormente con plantillas, para conseguir la forma de la sección tipo, en toda la
luz o por mitades.
Simulación
Referente a la interacción suelo-estructura, se modeliza en el programa mediante la
aplicación de las interfaces, suponiendo que
la superficie de contacto no es ni perfectamente lisa ni perfectamente rugosa. El grado de rugosidad del contacto se modeliza
eligiendo un valor adecuado para el factor de
reducción de la resistencia en la interfaz, que
se denomina Rinter. Este factor relaciona la
resistencia de la interfaz (fricción y adherencia de la pantalla) con la resistencia del suelo
(ángulo de fricción y cohesión).
Las fases consideradas en los modelos
tridimensionales han sido las siguientes:
Fase 1: Situación inicial
Fase 2: Ejecución galería de avance en
clave y entibación con tablas, puntales y tresillones de madera y longarinas metálicas.
Fase 3: Ensanche lateral de la galería de
avance hasta excavar sección completa de
bóveda.
Fase 5 a Fase 18: Repetición de fases
anteriores para simular el avance del túnel.
Fase 19-38: Excavación y ejecución por
bataches de los hastiales y la contrabóveda.
䡵
Proyecto de construcción de plataforma. Línea de alta velocidad Madrid-ZaragozaBarcelona-Frontera Francesa. Tramo La Torrassa- Sants
Para los modelos bidimensionales las fases
consideradas son las siguientes:
Fase 0.- Estado tensional inicial
Fase 1.- Excavación del avance del túnel.
Aplicación de relajación correspondiente al
avance. En esta fase, la excavación se simula
desactivando los elementos tipo soil y asignando un cierto nivel de relajación. Este escenario de relajación representa los desplazamientos uno hacia el interior del túnel debido a
la excavación producida por la tuneladora. De
hecho, en estas condiciones (2D y deformación plana) se puede mantener el análisis bidi-
Metodología seguida en las
simulaciones y simulaciones
realizadas
En cuanto a las condiciones de contorno,
adoptadas en el modelo son las habituales
para este tipo de cálculo. Los contornos lateral y posterior en cada uno de los modelos se
han situado a una distancia adecuada para
que las condiciones asignadas a los mismos
no influyan en los cálculos. El contorno anterior (en el sentido del eje del túnel) se ha alejado lo suficiente para obtener un régimen permanente con el que se estabilicen las deformaciones tras el avance secuencial. En estos
contornos se han fijado los desplazamientos
horizontales al estar suficientemente alejados.
Sobre las condiciones de contorno hidráulicas se fija el nivel freático inicial.
En cuanto a las condiciones iniciales, en el
modelo realizado se ha considerado como estado inicial del terreno el correspondiente a las
tensiones geoestáticas.
䡵 [Fig. 4].- Simulación mediante método Belga. Características del modelo utilizado.
20
184
Simulación
mensional si se supone la existencia de una
presión pi ficticia que su aplicación conduce al
mismo desplazamiento radial ui que en el
caso tridimensional. En este caso, la variación
continua desde pi = p0 (correspondiente a la
tensión inicial p0 de la Fase 0 del análisis) hasta pi = 0 reproduciría el complejo proceso de
deformación de una sección sin alterar por la
construcción del túnel (ui = 0) hasta en la sección sin revestimiento y alejada del frente de la
excavación.
En general, pi = 0 corresponde a una sección autoestable donde no habría presencia de
agua, ya que el criterio de las curvas características es en tensiones totales. Por este motivo, adoptando modelos constitutivos que no
admiten tracciones y considerando la presencia del nivel freático, habrá siempre que compensar el empuje de agua y, por tanto, la presión que deberá de equilibrar el sostenimiento
será como mínimo la del agua pi, último = pw
(hipótesis hidrostática).
La relación entre pi y ui constituye la denominada curva característica del túnel (CC) que
sólo depende de las características y condiciones en que se encuentra el terreno. En Plaxis
es posible utilizar la opción de construir por
etapas con un nivel último reducido de ΣMstage
en lugar de introducir un valor concreto de relajación (β). ΣMstage es un parámetro que va
de 0 a 1 que controla el equilibrio de fuerzas
en cada fase de cálculo y actúa de la siguiente manera:
donde:
Fuerza aplicada en la fase de
cálculo.
Fuerza al comienzo de la fase de
cálculo.
Fuerza definida en la fase de
cálculo.
De esta manera, cuando se desactivan los
dominios afectados por la excavación del túnel
se produce una presión no equilibrada inicial
que es comparable a la inicial (pk ). Al comienzo del cálculo la fase correspondiente a excavación (cuando ΣMstage es 0) esta presión se
aplica totalmente a la malla activa y disminuye
en cada iteración hasta 0 con el incremento simultáneo del parámetro ΣMstage hasta la unidad. De ahí nace la posibilidad de comparar
ΣMstage con 1-β y realizar las modelizaciones
con diferentes niveles de relajación del terreno.
En este punto hay que indicar que la presión remanente no equilibrada al final de esta
fase es aplicada inmediatamente después de
la colocación del sostenimiento, donde el parámetro ΣMstage es, por defecto y necesariamente, igual a la unidad.
Fase 2.- Ejecución de sostenimiento avance. Colocación del sostenimiento Y se deja
proseguir el cálculo hasta el equilibrio
(ΣMstage= 1). La colocación de este sostenimiento entra en carga al menos por dos motivos:
- El progresivo alejamiento del frente de excavación que supone la disminución virtual de la carga y por tanto un incremento de la deformación radial.
- Las deformaciones diferidas del terreno al
transcurrir el tiempo.
Entonces, teniendo en cuenta que el anillo
de sostenimiento se instala una vez el material
se ha relajado y deformado una magnitud ud la
respuesta del sostenimiento se puede escribir
de la siguiente manera:
La relación anterior es la que permite obtener la denominada curva de confinamiento
(CF) del sostenimiento, que depende fundamentalmente de la rigidez del anillo de dovelas
que actúa como sostenimiento (k). En la Fig. 6
se pueden ver de forma teórica la relación entre la curva característica y de confinamiento
del problema de una excavación.
El desplazamiento ud de la figura anterior
corresponde al desplazamiento obtenido después del cálculo de la Fase 1 (previa a la colocación del sostenimiento) mientras que el desplazamiento ueq corresponde al desplazamiento conjunto del terreno y sostenimiento una
vez colocado el último después del cálculo de
la Fase 2.
Fase 3.- Excavación de destroza del túnel.
Aplicación de relajación correspondiente a la
destroza.
Fase 4.- Ejecución de sostenimiento destroza.
Resultados obtenidos y comparación
con valores leídos en obras ya
ejecutadas
El punto más importante en un análisis de simulación en dos dimensiones del proceso de
la construcción de túneles con un revestimiento es tener en cuenta el efecto de arqueado tridimensional que se produce dentro del suelo y
las deformaciones que tienen lugar alrededor
de la parte no soportada de la sección.
En la bibliografía pueden encontrarse diferentes métodos para llevar a cabo este análisis. Uno de ellos es el denominado método β,
aunque otros autores han presentado métodos similares bajo diferentes nombres.
La idea consiste en descomponer las pre-
䡵 [Fig. 7]
.- Órdenes de magnitud obtenidos
por Schikora K., Fink T. (1982).
䡵 [Figura 6]
.- Forma teórica de la relación
entre la curva característica y de
confinamiento en una excavación.
䡵 [Figura 5]
.Representación
esquemática del
“β-method” para
el análisis de
túneles en el
programa Plaxis
v9.02.
21
142
siones iníciales pk que actúan en la situación
inicial sobre el contorno del futuro túnel en dos
partes: una de ellas se calcula como (1-β) pk
y se aplica al túnel no soportado; la otra es β
pk y se aplica al túnel soportado. El valor de β
se determina por lo general mediante métodos empíricos, que, entre otras cosas, consideran la relación entre la longitud de túnel no
soportada y el diámetro equivalente del túnel.
Los valores de β obtenidos para los casos
estudiados es el mostrado en la Fig. 8 (Sección tipo 1).
SECCIÓN TIPO 1
Los resultados de las simulaciones de este
apartado es posible compararlos con datos
de obras reales, concretamente: Proyecto de
construcción de plataforma. Línea de alta velocidad Madrid-Zaragoza-Barcelona-Frontera
Francesa. Tramo La Torrassa- Sants.
La sección utilizada coincide con la sección
Simulación
䡵 [Fig. 9]
.- Perfil geotécnico recogido en “Proyecto de construcción de
plataforma. Línea de alta velocidad Madrid-Zaragoza-BarcelonaFrontera Francesa. Tramo La Torrassa- Sants.”.
䡵
[Figura 8].- Salidas gráficas de resultados. Cálculos BT1001,
BT1002 y BT2001.
tipo 1 definida para este artículo, al igual el proceso constructivo que coincide con el utilizado
en las simulaciones (método Belga) y las coberteras y terrenos son también los empleados
en los cálculos.
En las Figs. 9 y 10 se recoge el perfil longitudinal del túnel utilizado para la comparación
de los resultados, así como la instrumentación
disponible y las medidas más representativas
que permitirán la citada comparación.
Para resumir la información, en la Fig. 11 se
muestra una tabla resumen con los resultados
más representativos y que se utilizarán a continuación para compararlos con los obtenidos
en las simulaciones numéricas.
De la interpretación de los resultados de los
cálculos realizados para la sección tipo 1 se
pueden sacar las siguientes conclusiones:
• Con los resultados obtenidos primeramente se ha estudiado el porcentaje que
supone el asiento obtenidos en la fase
䡵 [Fig. 10]
.- Ejemplo de auscultación disponible de las obras de construcción
de plataforma de la línea de alta velocidad Madrid-Zaragoza-BarcelonaFrontera Francesa. Tramo La Torrassa- Sants. Hitos 250.
de avance respecto al obtenido una vez
finalizado el túnel. En las simulaciones realizadas porcentaje obtenido es de entre
el 80 y el 92 %, adoptando un valor medio de 85 %.
El grado de correlación que se obtiene es
elevado aún no considerando variables
como la cobertera o material donde se
ejecuta el túnel, por lo que se puede concluir que el porcentaje de asientos en
avance respecto al total es independiente de la cobertera o características geo-
䡵 [Figura 11]
.Porcentaje de
asiento
avance/destroza
en método
Belga. Sección 1.
Datos de
simulaciones
comparados con
datos reales
medidos en obra.
22
142
Simulación
técnicas del material donde se excava el
túnel.
Para poder validar esta afirmación, así
como el rango obtenido en las simulaciones numéricas, se muestra en forma
de gráfico los valores obtenidos en las simulaciones y los datos de asientos reales leídos durante la ejecución de las
obras expuestas al comienzo del apartado, donde la sección de ejecución del
túnel es la misma, así como el procedimiento constructivo utilizado. Respecto
al material, como se ve en el perfil geotécnico el tramo comparado discurre básicamente por las arcilla marrones, la
cual se han realizado la mitad de las simulaciones.
A la vista de la comparación con los resultados reales se pueden destacar las
siguientes conclusiones:
o La relación entre el asiento obtenido
en fase de avance respecto al final
es independiente del material donde
se excava, de la longitud del pase y
de la cobertera, y se puede cifrar
esta relación en 0.8 (80%), con rango de variación entre 0.72-0.92.
• La disponibilidad de datos reales permite realizar una comparación entre los
asientos estimados en las simulaciones y
los asientos reales. Los materiales atravesados por el túnel en las simulaciones
están realizadas con un perfil homogéneo (arcillas marrones del cuaternario de
Barcelona) estando el perfil estratigráfico
real formado por arcillas marones apareciendo bajo la contrabóveda y junto a los
hastiales otros materiales que puede justificar la diversidad observada.
A los valores reales añadidos al gráfico
de los resultados de asientos medidos
en obra se han añadido 4 valores, correspondiente al asiento obtenido para la
sección de cálculos aplicando el método
semiempírico propuesto por Carlos Oteo
(método Madrid, ref 99), para compararlos con los resultados obtenidos en los
cálculo donde se han utilizado las denominadas arenas (similares a los terciarios
de Madrid).
Con todos estos datos se puede realizar
la comparación de los asientos simulados con asientos reales medidos en
obra y con asientos obtenidos con métodos semiempíricos los cuales a su vez
han sido calibrados con datos de obra,
obteniendo el gráfico de la Fig 12.
Como conclusión señalar que los valores
obtenidos para las simulaciones en las
arenas están dentro del rango establecido por el Modelo Madrid (OTEO et al,
䡵 [Figura 12]
.Comparativa de
asientos
obtenidos con
datos de
simulaciones y
datos reales
(arcillas) y datos
obtenidos con
métodos
semiempíricos.
Sección 1.
Método Belga.
1999) obtenido a partir de datos reales
en obra. Para el caso de las simulaciones realizadas sobre las denominada Arcillas marrones los datos obtenidos en
obra arrojan una gran dispersión. Como
explicación a esto se puede señalar que
el método belga presenta una elevada
especialización de la mano de obra de
cuya correcta ejecución (acuñado de tresillones, puntales de madera, etc) puede
variar la descompresión producida y por
tanto los asientos originados.
• Respecto a la influencia que tiene el
pase de excavación empleado en los
asientos originados en superficie (Fig.
13), los análisis realizados concluyen que
reducir la longitud de pase de 2.5 m (valor habitual en el método belga) a 1.25,
reduce los asiento un 19 % de media
(con reducciones comprendidas entre un
10 – 30 %).
• Respecto a las relajaciones, objetivo
principal de este apartado, los valores
obtenidos se muestran en gráfica de la
Fig. 14.
Tras el análisis de los resultados se pueden
destacar los siguientes comentarios:
o La relajación a considerar para los cálculos realizados no depende de la cobertera.
o Para las simulaciones realizadas, para
ref
terreno con un modulo E50 = 3000
t/m² y para una longitud de pase de
2.5 m ejecutado mediante método
Belga la relajación a considerar es de
0.3 para el avance y de 0.29 para la
ref
destroza, mientras que para un E50 =
13000 t/m² la relajación a considerar
es de 0.37 al avance y 0.32 para la
destroza.
o Para simular en un modelo 2D la reducción de pase en el método belga
(de 2.5 m a 1.25 m) esta se puede
conseguir reduciendo entre un 30 y 36
% la relajación considerada tanto en la
simulación del avance como en la simulación de la destroza.
o El valor de relajación a considerar en la
destroza es entre un 87 y un 94% del
valor considerado en el avance.
Para la sección tipo 2 las conclusiones obtenidas son las siguientes:
• Con los resultados obtenidos primeramente se ha estudiado el porcentaje que
supone el asiento obtenidos en la fase
de avance respecto al obtenido una vez
finalizado el túnel. En las simulaciones
realizadas el porcentaje está comprendido entre el 65 y el 85 %, adoptando un
valor medio de 75 % (Fig. 15).
Para poder validar esta afirmación, así
como el rango obtenido en las simula-
䡵 [Figura 13]
.Análisis de la
influencia de la
reducción de
pase en el
asiento
producido.
Sección 1.
Método Belga.
23
142
Simulación
䡵 [Figura 14]
.- Análisis de la relajación a considerar en método Belga (sección 1) en función
de la cobertera, longitud de pase y tipo de terreno.
A la vista de la comparación con los resultados reales se pueden destacar las
siguientes conclusiones:
o La relación entre el asiento obtenido
en fase de avance respecto al final es
independiente del material donde se
excava, de la longitud del pase y de la
cobertera, y se puede cifrar esta relación en 0.8 (80%), con rango de variación entre 0.72-0.92.
• Respecto a la influencia que tiene el
pase de excavación empleado en los
asientos originados en superficie, los
análisis realizados concluyen que reducir
la longitud de pase de 2.5 m (valor habitual en el método belga) a 1.25 reduce
los asiento un 21 % de media (con reducciones comprendidas entre un 7 –
30 %)
Tras el análisis de los resultados podemos destacar los siguientes comentarios:
o La relajación a considerar para los cálculos realizados no depende de la cobertera.
o Para las simulaciones realizadas, para
ref
terreno con un modulo E50 = 3000
t/m² y para una longitud de pase de
2.5 m ejecutado mediante método
Belga la relajación a considerar es de
0.36 para el avance y de 0.30 para la
ref
destroza, mientras que para un E50 =
13000 t/m² la relajación a considerar
es de 0.35 al avance y 0.32 para la
destroza.
o Para simular en un modelo 2D la reducción de pase en el método belga
(de 2.5 m a 1.25 m) esta se puede
conseguir reduciendo entre un 28 y 37
% la relajación considerada tanto en la
simulación del avance como en la simulación de la destroza.
o El valor de relajación a considerar en la
destroza es entre un 73 y un 94% del
valor considerado en el avance.
❖
䡵 [Figura 15]
.Comparativa de
porcentaje de
asientos avance
respecto a los
obtenidos en la
fase final. Datos
reales y datos de
simulaciones.
Sección 2.
Método Belga.
ciones numéricas, se añade al gráfico
expuesto los datos de asientos reales leídos durante la ejecución de las obras
expuestas al comienzo del apartado,
donde la sección de ejecución del túnel
es la misma, así como el procedimiento
constructivo simulado. Respecto al material, como se ve en el perfil geotécnico,
el tramo comparado discurre básicamente por las arenas terciarias con la
cual se han realizado la mitad de las simulaciones.
24
142
KV Consultores
i
Claudio Coello, 52 - 1ª Plta.
28001 Madrid
: 914 2611 715 • Fax: 915 759 587
E-mail: [email protected]
Web: www.kvconsultores.es