Sol1

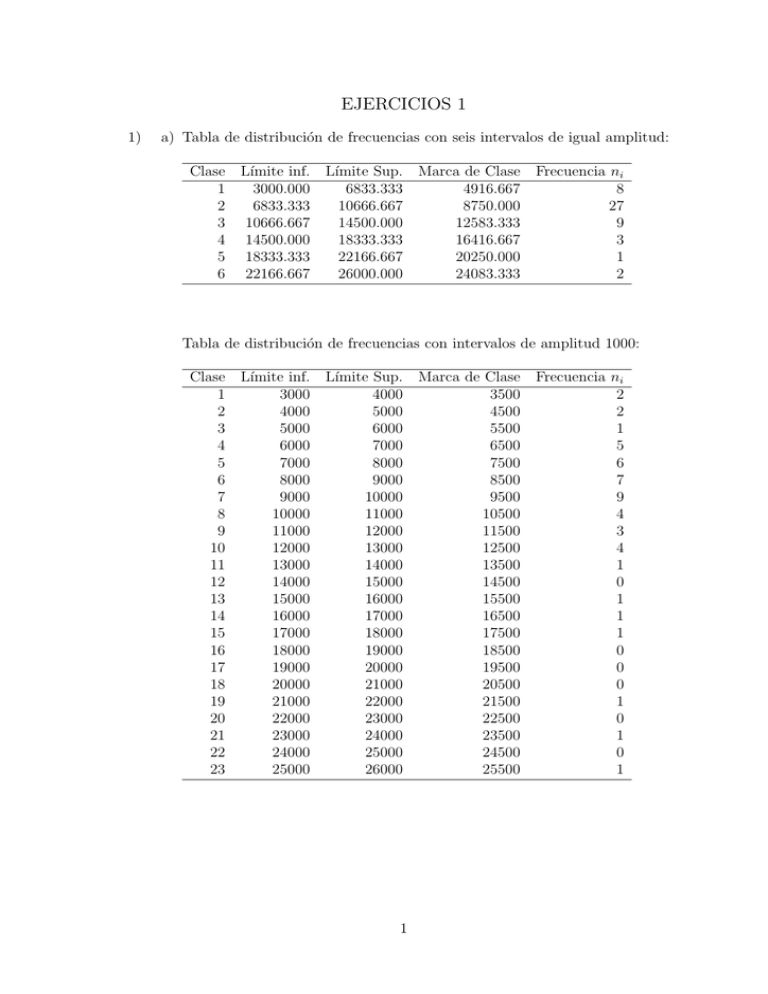
EJERCICIOS 1
1)
a) Tabla de distribución de frecuencias con seis intervalos de igual amplitud:
Clase Lı́mite inf. Lı́mite Sup. Marca de Clase Frecuencia ni
1
3000.000
6833.333
4916.667
8
2
6833.333
10666.667
8750.000
27
3 10666.667
14500.000
12583.333
9
4 14500.000
18333.333
16416.667
3
5 18333.333
22166.667
20250.000
1
6 22166.667
26000.000
24083.333
2
Tabla de distribución de frecuencias con intervalos de amplitud 1000:
Clase Lı́mite inf. Lı́mite Sup. Marca de Clase
1
3000
4000
3500
2
4000
5000
4500
3
5000
6000
5500
4
6000
7000
6500
5
7000
8000
7500
6
8000
9000
8500
7
9000
10000
9500
8
10000
11000
10500
9
11000
12000
11500
10
12000
13000
12500
11
13000
14000
13500
12
14000
15000
14500
13
15000
16000
15500
14
16000
17000
16500
15
17000
18000
17500
16
18000
19000
18500
17
19000
20000
19500
18
20000
21000
20500
19
21000
22000
21500
20
22000
23000
22500
21
23000
24000
23500
22
24000
25000
24500
23
25000
26000
25500
1
Frecuencia ni
2
2
1
5
6
7
9
4
3
4
1
0
1
1
1
0
0
0
1
0
1
0
1
b) Histograma de la distribución de frecuencias:
4
2
0
Frequency
6
8
Histograma de INGRESOS
5000
10000
15000
20000
INGRESOS
2)
a) Diagrama de tallo y hojas:
Unidad=1
1|2 representa 12
LO |18
2
8
13
34
(16)
36
25
15
5
3
1
3
3
4
4
5
5
6
6
7
7
8
|
|
|
|
|
|
|
|
|
|
|
0
577889
22333
555666666777889999999
0000111222233344
55556667889
0000122233
5666888999
02
56
0
2
25000
b) Tabla de frecuencias:
Clase Lı́mite inf.
1
10
2
20
3
30
4
40
5
50
6
60
7
70
Lı́mite Sup.
20
30
40
50
60
70
80
Marca de Clase Frecuencia ni
15
1
25
1
35
6
45
30
55
27
65
17
75
4
c) Polı́gono de frecuencias e histograma de la distribución de frecuencias:
15
10
5
0
Frequency
20
25
30
Polígono de frecuencias e Histograma de TEMPERATURAS
10
20
30
40
50
TEMPERATURAS
3
60
70
80
3)
a) Tabla para la distribución de frecuencias con 10 intervalos de amplitud 2.5 cm:
Clase Lı́mite inf. Lı́mite Sup. Marca de Clase
1
1.450
1.475
1.463
2
1.475
1.500
1.487
3
1.500
1.525
1.513
4
1.525
1.550
1.538
5
1.550
1.575
1.563
6
1.575
1.600
1.588
7
1.600
1.625
1.613
8
1.625
1.650
1.638
9
1.650
1.675
1.663
10
1.675
1.700
1.688
Frecuencia ni
2
3
3
10
8
9
9
5
0
1
b) Histograma de frecuencias:
6
4
2
0
Frequency
8
10
Histograma de ESTATURA
1.45
1.50
1.55
1.60
ESTATURA
4
1.65
1.70
4)
a) Tabla de distribución de frecuencias relativas:
Clase Lı́mite inf. Lı́mite Sup. Marca de Clase Frecuencia fi
1
0
3
1.5
0.42
2
3
6
4.5
0.26
3
6
9
7.5
0.15
4
9
12
10.5
0.08
5
12
15
13.5
0.04
6
15
18
16.5
0.03
7
18
21
19.5
0.02
Histograma:
0.08
0.06
0.04
0.02
0.00
Density
0.10
0.12
0.14
Histograma de TIEMPO
0
5
10
15
20
TIEMPO
b) Tabla de distribución de frecuencias acumuladas:
Clase Lı́mite inf. Lı́mite Sup. Marca de Clase Frecuencia Acumulada
1
0
3
1.5
210
2
3
6
4.5
340
3
6
9
7.5
415
4
9
12
10.5
455
5
12
15
13.5
475
6
15
18
16.5
490
7
18
21
19.5
500
5
Histograma de frecuencias acumuladas:
300
200
100
0
Frequency
400
500
Histograma de TIEMPO
0
5
10
15
TIEMPO
5)
a) Diagrama de tallo y hojas: Unidad=1
1|2 representa 12
1 1s |7
2 1o |9
5 2* |011
5 2t |
9 2f |4555
(4) 2s |6677
12 2o |88
10 3* |011
7 3t |22
5 3f |4
4 3s |6
3 3o |9
2 4* |1
HI
|43
6
20
b) Tabla de frecuencias:
Clase Lı́mite inf.
1
15
2
20
3
25
4
30
5
35
6
40
Lı́mite Sup.
20
25
30
35
40
45
Marca de Clase
17.5
22.5
27.5
32.5
37.5
42.5
Frecuencia ni
3
6
7
5
2
2
c), d) Cálculo de las frecuencias relativas:
ni
fi = P k
j=1
nj
,
donde k es el número de clases o intervalos definidos. Notemos que el denominador de la expresión es simplemente el número de observaciones (N =25).
Cálculo de las frecuencias acumuladas:
nai =
i
X
nj
j=1
Tabla de frecuencias:
Clase Lı́m. inf. Lı́m. Sup. Marca de Clase
1
15
20
17.5
2
20
25
22.5
3
25
30
27.5
4
30
35
32.5
5
35
40
37.5
6
40
45
42.5
7
Frec. rel. fi
0.12
0.24
0.28
0.20
0.08
0.08
Frec.Acumulada
3
9
16
21
23
25
6)
a) Histogramas de frecuencias:
3
0
1
2
Frequency
4
5
6
Histograma de TIEMPO (vez 10)
10
15
20
25
30
35
40
TIEMPO.10
4
2
0
Frequency
6
8
Histograma de TIEMPO (vez 30)
5
10
15
20
TIEMPO.30
b) Parece existir una relación entre el número de veces que se realiza una tarea y el
tiempo que se necesita para realizarla, pues notamos en los histogramas que los
intervalos más frecuentes son: 18-20, 8-10, y 6-8, respectivamente, señalándonos
que el tiempo necesario disminuye a medida que se incrementea el número de
veces que se realiza la operación. También, en cuanto a la tasa de disminución decreciente en el tiempo necesario, observamos que de 10 a 30 veces disminuimos aproximadamente 10 unidades, y de 30 a 50 veces, sólo disminuimos
en 2 unidades. Estas dos observaciones son congruentes con el enunciado.
8
4
2
0
Frequency
6
8
Histograma de TIEMPO (vez 50)
5
10
15
20
TIEMPO.50
7)
a) Diagrama de tallos y hojas:
Unidad=10
1|2 representa 120
1 0t |3
5 0f |4455
15 0s |6666677777
(10) 0o |8888999999
13 1* |111
10 1t |2222
6 1f |44
4 1s |7
HI
|21,25,27
b) El rango de la variable TIEMPO se ha dividido en 8 intervalos (los tallos),
siendo 30 y 170 los valores menor y mayor representados en el gráfico. Los
valores 210, 250 y 270 se consideran datos atı́picos. La mediana está entre 80
y 90.
8)
a) Tabla de distribución de frecuencias relativas:
Notemos que como datos nos dan ni (e.g. n1 = 14 corresponde a los 14 estudiantes Varones Casados de Derecho), de donde sumando, obtenemos N = 100,
y podemos calcular las fi como en el ejercicio 5. En este caso, “Lı́m.Inf” señala
la pertenencia a una categorı́a en cuestión (notemos que en la categorı́a 9 no
9
hay ningún estudiante).
Lı́m.Inf Frec.Relativa fi
1
0.14
2
0.16
3
0.10
4
0.05
5
0.19
6
0.04
7
0.05
8
0.12
9
0.00
10
0.05
11
0.08
12
0.02
b) Tablas para la distribución de frecuencias:
Sexo
Carrera
Lı́m.Inf Frec.Rel. fi
M
32
V
68
Lı́m.Inf Frec.Rel. fi
Derecho
29
Lade
55
Lec
16
10
Estado civil
Lı́m.Inf
Casado
Soltero
Frec.Rel. fi
57
43