Tutorial introductorio al Lenguaje Abel

UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
Tutorial introductorio al Lenguaje Abel ( Advanced Bolean Equations
Language).
1.Lenguaje Abel.
2.Estructura básica de un programa Abel.
2.1 Encabezado.
2.2 Declaraciones.
2.3 Descripción lógica.
2.3.1 Bloques de ecuaciones.
2.3.2 Tablas de verdad.
2.3.3 Diagrama de estados
2.3.3.4 Representación de máquinas secuenciales.
2.4 Vectores de Test.
3.Links y referencias
1. Lenguaje Abel
Abel es un lenguaje de descripción de hardware (HDL) que permite:
1. Describir un circuito digital.
2. Definir vectores de test para comprobar el funcionamiento del código
generado.
3. Generar un archivo .SVF .JEDEC para quemar un dispositivo lógico
programable como son los PLD y CPLD.
A continuación se presenta un compendio de los aspectos más relevantes de este
lenguaje. Esto no pretende ser una discusión completa que permita al lector
profundizar sus conocimientos. Si Usted ya está familiarizado con el lenguaje, este
escrito sólo le servirá como repaso.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
1
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
2.Estructura básica de un programa Abel.
A continuación se presenta en la tabla 1 la estructura típica de un programa Abel.
Tabla 1
Estructura típica de un
Programa en Abel.
Encabezado
Module module_name
title string
Declaraciones
DeviceID device
deviceType
Declaraciones de pin
otras declaraciones
Descripción lógica
Equations
Ecuaciones
Vectores de Test
test_vectors
vectores de test
end module_name
2.1 Encabezado.
Tiene las siguientes palabras claves.
•
Palabra clave: module.
Esta palabra clave es necesaria pues indica el nombre y el comienzo del módulo.
Debe ir siempre un END al final del modulo. Programas largos pueden tener varios
módulos, cada uno con su propio nombre, título, declaraciones y ecuaciones.
•
Palabra clave: title.
Especifica un string de título que será incluido en los archivos de documentación
generada por el compilador.
•
Los comentarios se agregan comenzando el texto con comillas dobles.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
2
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
2.2 Declaraciones.
A esta área corresponden los siguientes aspectos.
• Palabra clave: device.
La declaración device es opcional e incluye un identificador y un string que denota
el tipo de dispositivo. El compilador usa el nombre del dispositivo, para verificar que este
soporta las ecuaciones lógicas especificadas en el programa.
•
Palabra clave: pin (pin declaration)
Las declaraciones de pin informan al compilador acerca de los nombres asociados a
los pines del componente. Si el nombre de la señal declarada está precedida por un NOT
(!), entonces en el pin asociado se presentará el complemento de la señal en cuestión.
•
Palabra clave: node.
Se usa para declarar señales que no son conectadas a pines externos.
•
Palabra clave: istype.
Define una lista de atributos de una señal. Se puede usar después de una declaración
de pin o node. En el manual de referencia (pág 51) se encuentra una lista de atributos que
resulta interesante revisar. Un ejemplo es la palabra clave com que define una salida
combinacional.
•
Uso de range.
Un rango de nombre de señales puede definirse con el primer y último nombre de
del rango separados por ..., por ejemplo “L0...L5”.
•
Uso de Set.
Un Set es un conjunto de señales o constantes referenciadas con un solo nombre.
Cada operación aplicadas al Set es aplicada a cada una de las señales que lo componen.
•
También es posible declarar constantes y expresiones que pueden simplificar el
programa.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
3
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
2.3 Descripción Lógica.
Un diseño lógico puede ser descrito de las siguientes maneras:
1. Bloques de ecuaciones.
2. Tablas de verdad.
3. Diagrama de estados.
2.3.1Bloques de ecuaciones.
Se utiliza la palabra clave equations para comenzar la descripción lógica. Las
ecuaciones se especifican con expresiones lógicas utilizando operadores o bloques “WhenThen-Else”.
Alguno de los operadores son los siguientes:
&
#
!
$
!$
Ejemplo 1.
En este ejemplo
Podemos revisar
algunos conceptos
ya conocidos.
AND
OR
NOT
XOR
XNOR
MODULE V7408
" Quad two input AND gate. Cuatro
ands de dos entradas.
" Declaraciones de señales de entrada
A0, A1, B0, B1, C0, C1, D0, D1 PIN;
" Declaraciones de señales de salida. Se
requiere definir un tipo de salida.
YA, YB, YC, YD PIN istype 'com';
EQUATIONS
YA = A0 &
YB = B0 &
YC = C0 &
YD = D0 &
A1;
B1;
C1;
D1;
END
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
4
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
2.3.2 Tablas de verdad.
Es otra manera de especificar funciones combinaciones lógicas. La forma general
de utilizar esta característica se muestra en la tabla 2.
Tabla 2
Estructura general
de una tabla de verdad
truth_table (input-list -> output-list)
input-value -> output-value;
....
input-value -> output-value;
Como se observa en la tabla 2 la tabla de verdad debe ir precedida por la palabra
clave truth_table. Las palabras input_value y output_value son los nombres de las
señales de entrada y salida de la tabla. En el ejemplo presentado en la tabla 3 se ilustra la
definición de una función mediante tablas de verdad.
Tabla 3
Definición de
una función mediante
tablas de verdad.
" Función de tres variables.
MODULE f3
" entradas
a, b, c PIN;
" salidas
f PIN ISTYPE 'COM';
EQUATIONS
truth_table ( [a, b, c]->f )
[0, 0, 0]-> 0;
[0, 0, 1]-> 1;
[0, 1, 0]-> 0;
[0, 1, 1]-> 1;
[1, 0, 0]-> 0;
[1, 0, 1]-> 0;
[1, 1, 0]-> 1;
[1, 1, 1]-> 1;
Test_vectors ( [a, b, c]->f )
[0, 0, 0]-> 0;
[0, 0, 1]-> 1;
[0, 1, 0]-> 0;
[0, 1, 1]-> 1;
[1, 0, 0]-> 0;
[1, 0, 1]-> 0;
[1, 1, 0]-> 1;
[1, 1, 1]-> 1;
END
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
5
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
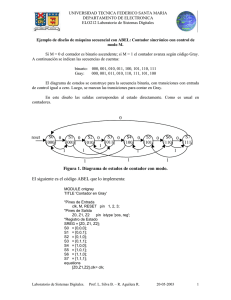
2.3.4 Diagramas de estado.
En un sistema secuencial, para poder generar la salida en un tiempo dado, es preciso
conocer valores previos de algunas variables. No bastan los valores presentes de la entrada.
Es decir, debe almacenarse información concerniente a los valores de las entradas pasadas,
para poder generar la salida a partir de la entrada presente y los valores almacenados.
La información anteriormente mencionada, se almacena en estados internos. Los valores
que deben registrarse para recordar la situación, debida a los valores de las entradas
pasadas, se almacena en variables de estado.
En cualquier instante, una máquina secuencial está en uno de un número finito de
estados; éstos quedan determinados por el valor de las variables de estado. En la figura 1
podemos ver un esquemático de lo anterior.
2.3.3.4 Representación de máquinas secuenciales
Se entiende por representación, la descripción de cómo se pasa de un estado a otro,
debido a los cambios de las entradas. Las representaciones deben describir en forma precisa
y completa a la máquina.
Modelo de Mealy
Es un modelo secuencial en el cual la salida está asociada a las transiciones entre
estados. Las salidas y el próximo estado cambian instantáneamente con los cambios de las
entradas.
Diagrama de estados: Como muestra la figura 2, los estados se representan mediante
círculos, y por líneas rotuladas y orientadas a las transiciones.
El rótulo indica la entrada y la salida que provoca la transición. Se separan con un slash.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
6
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
El diagrama de estados de la figura 2 se lee: Estando en el estado y, cuando llega la
entrada x se pasa al estado Y, con salida z.
A continuación se tiene en la figura 3 el diagrama de estados de una máquina
secuencial (Modelo de Mealy) que produce una salida alta cada vez que se detecta la
secuencia 0101 en la entrada; y salida cero en el resto de los casos.
En la tabla 4 se muestra el código en Abel para esta máquina de estrados.
En las declaraciones se emplea el tipo reg, para declarar una salida registrada; es decir, una
salida de un flip-flop D. En el diseño se tienen dos salidas: z es una salida combinacional,
asincrónica; mientras que la salida zs es de tipo sincrónica.
Luego se declara el registro de estado(sreg), en función de las salidas de los flip-flops.
También se efectúa un mapeo de nombres lógicos a físicos. Esto también se denomina
asignación de estados.
El estado inicial, será el estado A; cuyo nombre binario será [0, 0].
En las ecuaciones se indican las señales de entrada que ingresan al reloj(clock), a la
habilitación de la salida(enab, no se usa enable ya que es palabra reservada) y al reseteo
asincrónico de la macrocelda(reset).
Luego se describe el diagrama de estados de sreg, mediante la especificación de cada
estado.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
7
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
En este se indican las transiciones de acuerdo a los valores de las entradas(esto se indica
con la sentencia if then else); y los valores que deben tomar las salidas(esto se realiza con la
sentencia with).
Debe notarse que las salidas registradas se asignan con :=, y que a las salidas
combinacionales se les asigna un valor con el signo igual. Pueden agruparse acciones,
mediante el uso de paréntesis cursivos{ }.
Finalmente se especifican vectores de prueba. Se emplea la constante .c. para modelar un
pulso de reloj.
Tabla4
Ejemplo de máquina
de estados
MODULE estado1
TITLE 'Diagrama de Estados. Modelo
de Mealy'
"Declaraciones
q1, q0, zs pin istype 'reg';
"Estado y Salida Registrada
clock, enab, reset, x pin ;
"Entradas z pin istype 'com';
"Salida Combinacional.
sreg = [q1,q0];
"Valores de los estados
A= 0; B= 1; C= 2; D= 3;
equations
[q1,q0,zs].clk= clock;
[q1,q0,zs].oe = !enab;
[q1,q0,zs].ar = reset; "Con reset
va a [0, 0](el estado A).
state_diagram sreg;
State A:
zs := 0;
if (!x) then B with z =
with z = 0;
State B:
if (!x) then B with z =
with z = 0;
State C:
if (!x) then D with z =
with z = 0;
State D:
if (!x) then B with z =
with {z = 1; zs := 1;}
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
0; else A
0; else C
0; else A
0; else C
8
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
test_vectors ( [clock,enab,reset, x]->[sreg,zs])
[.c. , 0 , 1 , 0 ]->[A ,0];
[.c. , 0 , 0 , 1 ]->[A ,0];
[.c. , 0 , 0 , 0 ]->[B ,0];
[.c. , 0 , 0 , 1 ]->[C ,0];
[.c. , 0 , 0 , 0 ]->[D ,0];
[.c. , 0 , 0 , 1 ]->[C ,1];
[.c. , 0 , 0 , 1 ]->[A ,0];
[.c. , 0 , 0 , 0 ]->[B ,0];
[.c. , 0 , 0 , 0 ]->[B ,0];
[.c. , 0 , 0 , 1 ]->[C ,0];
[.c. , 0 , 0 , 1 ]->[A ,0];
END
Como observamos el diagrama de estado contiene la descripción de estado para el diseño
lógico.
La sintaxis para un diagrama de estados se muestra en la tabla 5.
Tabla 5
Sintaxis de un
diagrama de estados.
•
•
state_diagram state_reg
STATE state_value : [equation;]
[equation;]
:
:
trans_stmt ; ...
La palabra clave state_diagram indica el comienzo de la descripción de una
máquina de estados.
La palabra clave STATE y todas las que se describen a continuación, describen
un estado del diagrama de estados. En particular STATE da al estado un nombre
o valor
• state_reg: es un identificador que define la señal que determina el
estado de la máquina.
• state_value: puede ser una expresión, un valor o un nombre
simbólico del estado.
• equation: define las salidas de la máquina de estado.
• tran_stmt: define el próximo estado.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
9
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
Modelo de Moore
Modelo secuencial en el cual la salida sólo está asociada al estado presente. Las
salidas cambian sólo en cantos de sincronización del reloj.
El diagrama de estados asociado a este modelo se presenta en la figura 4.
Estando en estado y, con salida z; cuando ocurre la entrada x se pasa al estado Y,
con salida z2. La salida no cambia en la transición. Por esta razón, las salidas se asocian a
los estados.
A continuación se presenta un reconocedor de un patrón finito. Modelo de Moore
Sean: entrada x y salida z. La salida se activa cada vez que se presenta la secuencia 010, y
mientras que la secuencia 100 no se haya presentado, en cuyo caso la salida se desactiva
permanentemente. El diagrama de estados está representado en la figura 5.
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
10
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
El diseño queda implementado por el programa Abel ilustrado la tabla 5.
Tabla 5
MODULE fsm010
TITLE 'fsm010'
"Activa Z cada vez que llega 010 y
mientras no llegue 100.
"si llega 100 se activa Y, y permanece
en ese estado.
"Declaraciones
"Pines de entrada
clk, Xin, RESET pin;
"Pines de Salida
Q0, Q1, Q2 pin istype 'reg';
Z, Y pin istype 'com';
"Registro de Estado
SREG = [Q0, Q1, Q2];
"Definicion de Estados
S0 = [0,0,0]; " Estado Inicial.
state)
S1 = [0,0,1]; " secuencias tipo
S2 = [0,1,0]; " secuencias tipo
S3 = [0,1,1]; " secuencias tipo
S4 = [1,0,0]; " secuencias tipo
S5 = [1,0,1]; " secuencias tipo
S6 = [1,1,0]; " secuencias tipo
(Reset
...0
...01
...010
...1
...10
...100
equations
[Q0,Q1,Q2].clk= clk;
[Q0.ar, Q1.ar, Q2.ar] = RESET; "Con
Reset va a S0
" Z=!Q0&Q1&Q2; Y=Q0&Q1&!Q2;
"Modelo de Moore
state_diagram SREG
state S0: Z=0; Y=0; if Xin then S4 else
S1;
state S1: if Xin then S2 else S1;
state S2: if Xin then S4 else S3;
state S3: Z=1; if Xin then S2 else S6;
state S4: if Xin then S4 else S5;
state S5: if Xin then S2 else S6;
state S6: Y=1; goto S6;
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
11
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
test_vectors ([clk, RESET, Xin] -> [Z,Y])
[.C.,1,.X.] ->[0,0]; "reset
[.C.,0, 0] -> [0,0];
"secuencia 00101010010
[.C.,0, 0] -> [0,0];
[.C.,0, 1] -> [0,0];
[.C.,0, 0] -> [1,0];
[.C.,0, 1] -> [0,0];
[.C.,0, 0] -> [1,0];
[.C.,0, 1] -> [0,0];
[.C.,0, 0] -> [1,0];
[.C.,0, 0] -> [0,1];
[.C.,0, 1] -> [0,1];
[.C.,0, 0] -> [0,1];
END fsm010;
2.4 Vectores de prueba
Como se ha observado en muchos de los ejemplos entregados. Abel posee un
sistema opcional de vectores de prueba. El formato general de los vectores de test es similar
a las tablas de verdad y se muestra en la tabla 5.
Tabla 6
Estructura general
de los vectores de prueba
test_vectors (input-list -> output-list)
input-value -> output-value;
...
input-value -> output value;
Como se observa en la tabla 6 la tabla de vectores de test debe ir precedida por la
palabra clave test_vectors. Las palabras input_value y output_value dan los nombres a
las señales de entrada y salida de los vectores de prueba.
Para profundizar un poco más en la gran utilidad de estos vectores de prueba,
volvamos al ejemplo 1 de la pág. 4. Para este ejemplo podríamos escribir el siguiente
conjunto de vectores de prueba.
Test_vectors
( [A1, A0 ]
[0, 0]
[0, 1]
[1, 0]
[1, 1]
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
-> [YA])
->[ 0 ];
->[ 0 ];
->[ 0 ];
->[ 1 ];
12
UNIVERSIDAD TECNICA FEDERICO SANTA MARIA
DEPARTAMENTO DE ELECTRONICA
ELO212 Laboratorio de Sistemas Digitales
Cada renglón define un vector, asignando valores a las entradas y salidas. La
primera línea, entre paréntesis redondos, muestra los identificadores de las señales de
entrada a la izquierda de la asignación; y la o las señales de salida a la derecha. Luego
vienen los valores de las entradas que se desea probar y la o las correspondientes salidas
que se desean verificar.
La simulación funcional aplica en las entradas los estímulos y calcula mediante las
ecuaciones o tablas de verdad los valores de las salidas; y revisa que éstos coincidan con las
salidas asignadas a cada uno de los vectores. Al final resume si las diferentes pruebas
pasaron o no.
AA Y
0 1 A
V0001
V0002
V0003
V0004
4
0
1
0
1
0
0
1
1
L
L
L
H
out of 4 vectors passed.
Efectuada la simulación temporal puede obtenerse la forma de onda de la salida (figura 6),
para los estímulos descritos en los vectores, las cuales muestran el retardo de propagación
del canto de subida de la señal de salida(YA):
3. Links y referencias.
•
Referencias
•
•
•
•
Xilinx-ABEL Design Software Reference Manual, Data I/O Corp., 1993.
The ABEL Hardware Design Language , 1999 by John F. Wakerly.
ABEL-HDL Reference Manual, Data I/O Corporation., 1999.
Links
•
•
http://www.elo.utfsm.cl/~lsb/elo211/aplicaciones/Pennsylvania/HDLABEL%20Primer.htm#State
http://www.elo.utfsm.cl/~lsb/elo211/elo211.html
Laboratorio de Sistemas Digitales.
Prof. Leopoldo Silva Bijit.
30-12-2002
13