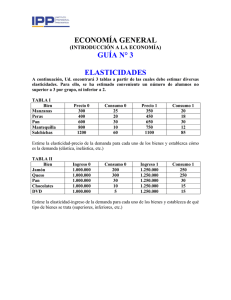
Soluciones del examen de julio

EXAMEN DE TÉCNICAS PARA EL ANÁLISIS DEL MERCADO. 3-Julio-2014.
APELLIDOS:
DNI:
NOMBRE:
1. La producción de piezas de una factoría se realiza en dos máquinas. El 40% de las piezas las produce la
máquina M 1 y el 60% restante la máquina M 2 .
a) (1 punto) Se decide tomar una muestra aleatoria estratificada de 200 piezas, con asignación
proporcional, para hacer un control de calidad. ¿Cuántas piezas producidas por cada máquina
deben examinarse?
Se toma la anterior muestra, obteniéndose los siguientes porcentajes de piezas defectuosas en cada
máquina:
máquina
Proporción muestral (en %)
10
M1
20
M2
b) (1 punto) Estime la proporción de piezas defectuosas de la factoría y el límite del error de
estimación.
c) (1 punto) Quiere repetirse el control de calidad sólo en la máquina M 2 para estimar el porcentaje
de piezas defectuosas con un error inferior al 2%. ¿Cuántas piezas producidas por esta máquina
habría que examinar?
2. Un fabricante de sierras quiere estimar el coste medio de reparación mensual para las sierras que ha
vendido a numerosas industrias. El fabricante no puede obtener un coste de reparación para cada sierra,
pero puede obtener la cantidad total gastada mensualmente en reparación y el número de sierras que tiene
cada industria. Entonces decide usar muestreo por conglomerados, con cada industria como un
conglomerado. El mes pasado el fabricante seleccionó una muestra aleatoria simple de 7 de las
muchísimas industrias a las que da servicio. Los datos sobre coste total de reparaciones por industria y el
número de sierras fueron:
Industria Nº sierras Coste total de reparación
para el mes pasado (€)
1
3
50
2
7
110
…
…
…
7
5
75
a) (2 puntos) Estime el coste medio de reparación por sierra para el mes pasado y el límite para el
error de estimación.
Use las siguientes sumas para realizar los cálculos necesarios.
Industrias
Sierras Coste (Sierras)2 (Coste)2
Sierras×Coste
1
3
50
9
2500
150
2
7
110
49
12100
770
...
...
...
...
...
...
7
5
75
25
5625
375
SUMA
43
755
325
104425
5745
b) (1 punto) Se quiere repetir el estudio con un error de estimación inferior a 1€. ¿Cuántas industrias
deberían observarse?
3. Se quiere conocer el número de enfermos que utilizan el Servicio de Urgencias de un hospital. Para ello,
de un mes (30 días) se seleccionaron al azar 3 días, observándose que 4320 personas usaron el servicio
durante dicho tiempo.
a) (1 punto) Estime con un intervalo de confianza el nº de enfermos/hora que acudieron al servicio
de urgencias.
b) (1 punto) Si se quisiera repetir en el próximo mes el mismo estudio, garantizando para la anterior
estimación un error inferior a un enfermo/hora, ¿cuantos días deberíamos observar?
4. Se han clasificado con un análisis cluster no jerárquico varios países en dos grupos (conglomerados)
según las variables (tipificadas): densidad de población, personas alfabetizadas, producto interior bruto,
tasa natalidad y fertilidad. Se ha obtenido la siguiente información:
Centros de los conglomerados finales
Habitantes por Km2
Personas Alfabetizadas (%)
Producto interior bruto per-cápita
Tasa de natalidad (por 1000 habitantes)
Fertilidad: número promedio de hijos
Conglomerado
1
2
,29562 -,39622
-,10044
,48451
,20101
,24467
-,99554
,89820
-,80460
,80460
ANOVA
Conglomerado
Media
cuadrática
gl
Habitantes por Km2
1,546
Personas Alfabetizadas (%)
1,105
Producto interior bruto per-cápita
,006
Tasa de natalidad (por 1000 hab.)
11,586
Fertilidad: número promedio de hijos
8,366
1
1
1
1
1
Error
Media
cuadrática
,914
,336
,698
,515
,310
gl
11
11
11
11
11
F
1,691
3,286
,009
22,477
26,951
Sig.
,220
,097
,927
,001
,000
a) (1 punto) ¿Respecto de qué variables existen diferencias significativas entre los dos grupos de
países que se han formado?
b) (1 punto) ¿En qué sentido son diferentes?
SOLUCIONES:
1.N1
N2
= 0, 40
= 0,60 n = 200 ⇒ n1 = 0, 40n = 80 n2 = 0,60n = 120
a)
N
N
b)
L
L
Ni 
p = 1
p =
N
p i = ( 0, 40 × 0,10 ) + ( 0,60 × 0, 20 ) = 0,16
∑
∑
i i
st
N i 1 =i 1 N
=
L
N i2 p i q i
1 L 2 p i q i N i − ni


=
=
=
V ( p st )
N
∑
∑
i
2
N 2 i 1=
ni − 1 N i
=
i 1 N ni − 1
2 V ( p st ) = 0, 0516
0,10 × 0,90  
0, 20 × 0,80 

2
=  0, 402 ×
 +  0,60 ×
 = 0,000666
79
119

 

pq 0, 20 × 0,80
B2
= 0, 0001 ⇒ n =
=
= 1600
c) B = 0, 02 D =
4
D
0, 0001
2.a)
n
n
n
n
n
=
=
7=
∑ mi 43=
∑ mi2 325
∑ yi 755
∑ yi2 104425=
∑ mi yi 5745
n
=i 1 =i 1 =i 1 =i 1
=i 1
n
=
y= µ
y
∑
i
= 17,5581 €
∑ mi
i =1
n
i =1
n
n
2
2
1 n
1  n 2

2
2
yi − ym=
y
y
m
y
mi =
yi 
+
−
∑
∑
∑
∑
i
i
i

n −1 i 1
n − 1  i 1 =i 1 =i 1
=
=

(
Sc
=
2
=
b)
)
(
)
1
104425 + (17,55812 × 325) − ( 2 × 17,5581 × 5745
=
) 479, 2771
6
43
1 N − n Sc2
1 Sc2

M= m= = 6,1429
V ( y=
)
=
= 1,8145
2
7
N n M2 n
M
N σ c2
=
=
n
ND + σ c2
{N → ∞=
}
σ c2
479, 2771
=
= 50,8 ≈ 51
D
9, 4338
2 V ( y =
) 2,694 €
2
B2 M
6,14292
=
=
= 9, 4338
D
4
4
3.n 3
=
a 1 dia
=
= 24 horas
m
=
n
∑ m=
i =1
i
4320
m
=
m
= 1440
n
m m 1440
λ
60
= =
= 60 enfermos / hora
V λ= =
= 0,8333
na a
24
an 24 × 3
( 60  1,8257 ) = ( 58,1743 , 61,8257 )
λ
60
4 × 60
b) 2 V λ =1 ⇒ 4V λ =1 ⇒ 4
=4
=1 ⇒ n =
=10
24 × n
24
an
( )

a) λ=
( )
( )
2 V λ= 1,8257
( )
4.a) Tasa de natalidad y fertilidad (niveles de significación 0,001 y menor que 0,001 respectivamente).
b) Los países del primer conglomerado tienen una tasa de natalidad y fertilidad por debajo de la media
mientras que los países del segundo conglomerado tienen una tasa de natalidad y fertilidad por encima de
la media.
EXAMEN CON ORDENADOR DE TÉCNICAS PARA EL ANÁLISIS DEL MERCADO. 3-Julio-2014
APELLIDOS:
NOMBRE:
DNI:
1
Para cada problema responda solamente los valores pedidos, dentro de los recuadros que aparecen a continuación con
el número de cada problema. Dar todas las soluciones (salvo k) con cuatro decimales, sin redondear, aunque se trate de
valores enteros como tamaños muestrales.
1.a.
1.b.
2.a.
2.b.
3.a.
3.b.
4.
4.
5.a.
5.b.
I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)I I I
(1 punto)I I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)
( 27033,0474 , 152996,9526 )
n=207,8675
k=9
(72,2112 , 73,5554)
(72,1802 , 73,5865)
(1534,1819 , 1949,9321)
(965,2120 2181,4547)
τ = 7526,3158
B=1090,3311
τ t = 6500
B=1532,5892
(2,7770 , 2,9530)
(68177,9453 , 75072,0547)
1.
Los responsables de un museo están interesados en el número total de personas que visitaron el
lugar durante 360 días que duró una exposición de una costosa colección de antigüedades. Puesto que el
control de visitantes en el museo todos los días es muy complejo, decidieron obtener estos datos cada
veinte días. La información de esta muestra sistemática de 1 en 20 se resume en la siguiente tabla:
Día Nº personas que visitan el museo
3
260
23
350
43
225


343
390
n
n
=
=
∑ yi 4500
∑ yi2 2610000
=i 1 =i 1
Con un nivel de confianza del 99%:
1.a. Estime con un intervalo de confianza el número de personas que visitaron el museo durante la
exposición de antigüedades.
1.b. Se quiere repetir el anterior estudio en una exposición similar que durará 2000 días con un error de
estimación inferior a 100000 visitantes. ¿Qué muestra sistemática deberá observarse en este caso?
Indique n y k (Utilice la muestra anterior para estimar los parámetros necesarios).
2.
Una verificación de control de calidad estándar para baterías de generadores de energía eólicos
consiste simplemente en registrar su peso. Un embarque particular de una fábrica consistió en las baterías
producidas en dos meses diferentes, con el mismo número de baterías producidas en cada mes. El
investigador decide estratificar con base en meses para el muestreo de inspección a fin de observar la
variación mensual. Las muestras aleatorias simples de los pesos de las baterías para los dos meses dieron
las siguientes mediciones (en kilos):
Mes A Mes B
72,5
74,5
72,5
73,8
73,5
73,5
74,0
70,5
73,8
70,5
74,5
71,0
Con un nivel de confianza del 90%, estime con un intervalo de confianza el peso medio de las baterías del
embarque utilizando:
2.a. Muestreo aleatorio estratificado.
2.b. Muestreo aleatorio simple.
3.
Se desea estimar el consumo mensual de una ciudad formada por 7000 familias. Se sabe que los
ingresos en dicha ciudad, vía declaración de la renta, ascienden a 17000000 € mensuales. Se realiza una
encuesta entre 6 hogares elegidos al azar y los resultados de renta y consumo se recogen en esta tabla.
Renta Consumo
2702,44
1840
2339,56
1500
981,06
800
2537,04
1600
1519,85
1200
3080,19
2500
Con un intervalo de confianza del 99%, estime el consumo mensual medio por hogar mediante:
3.a. Estimador de razón.
3.b. Muestreo aleatorio simple.
4.
El gerente de un periódico desea estimar el número de ejemplares comprados cada semana por las
familias de una localidad. Los 5500 hogares están agrupados en 500 edificios. Se tiene una encuesta
piloto en la cual se seleccionó una muestra de 4 edificios y se entrevistaron a todas las familias de estos
edificios, obteniéndose los siguientes resultados:
Edificio
Periódicos comprados cada semana por familia
1
2
3
0
3
0
2
1
4
1
1
2
1
0
2
1
2
3
1
1
2
3
2
1
1
1
1
0
2
1
3
1
1
4
1
1
0
2
1
0
3
0
Con un nivel de confianza del 90%, estime por los dos métodos el número de periódicos vendidos en
dicha localidad y el límite para el error de estimación.
5.
La policía de Madrid está interesada en conocer el número de manifestantes que se reunieron en la
Puerta del Sol. Con este dato se puede conocer la cuantía de medios materiales y humanos (policía,
protección civil, personal sanitario, etc.) necesaria para atender futuras concentraciones. Para estimar el
número de manifestantes se toma una fotografía aérea de la zona ocupada por éstos, tras lo cual se traza
sobre ella una cuadrícula que divide el área total en 250 cuadros de 10 metros de lado cada uno.
Posteriormente se numeran y se extrae una muestra aleatoria de 10 de estos cuadros; por último se cuenta
el número de manifestantes que hay en cada uno de los cuadros seleccionados, obteniéndose los
resultados de la tabla:
Nº del cuadro
5.a
5.b
Número de manifestantes en el cuadro
1
203
2
316
3
300
4
263
5
309
6
295
7
302
8
274
9
305
10
298
Estime la densidad de manifestantes por metro cuadrado con un intervalo de confianza del 90%.
Estime el número total de manifestantes concentrados en la Puerta del Sol con un intervalo de
confianza del 99%.
EXAMEN CON ORDENADOR DE TÉCNICAS PARA EL ANÁLISIS DEL MERCADO. 3-Julio-2014
APELLIDOS:
NOMBRE:
DNI:
2
Para cada problema responda solamente los valores pedidos, dentro de los recuadros que aparecen a continuación con
el número de cada problema. Dar todas las soluciones (salvo k) con cuatro decimales, sin redondear, aunque se trate de
valores enteros como tamaños muestrales.
1.a.
1.b.
2.a.
2.b.
3.a.
3.b.
4.
4.
5.a.
5.b.
I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)I I I
(1 punto)I I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)I
(1 punto)
(6680,6843 , 133319,3166)
n=334,0232
k=5
(83,4629 ,84,8038)
(83,4888 , 84,7779)
(1594,2346 , 1983,9316)
(2026,6613 , 2786,6720)
τ = 12315,7895
B=891,0030
τ t = 10800
B=1447,9738
(2,9483 , 3,1297)
(101394,738 , 111335,262)
1.
Los responsables de un museo están interesados en el número total de personas que visitaron el
lugar durante 260 días que duró una exposición de una costosa colección de antigüedades. Puesto que el
control de visitantes en el museo todos los días es muy complejo, decidieron obtener estos datos cada
veinte días. La información de esta muestra sistemática de 1 en 20 se resume en la siguiente tabla:
Día Nº personas que visitan el museo
3
260
23
350
43
225


243
390
n
n
=
=
∑ yi 3500
∑ yi2 2410000
=i 1 =i 1
Con un nivel de confianza del 99%:
1.a. Estime con un intervalo de confianza el número de personas que visitaron el museo durante la
exposición de antigüedades.
1.b. Se quiere repetir el anterior estudio en una exposición similar que durará 2000 días con un error de
estimación inferior a 90000 visitantes. ¿Qué muestra sistemática deberá observarse en este caso?
Indique n y k (Utilice la muestra anterior para estimar los parámetros necesarios).
2.
Una verificación de control de calidad estándar para baterías de generadores de energía eólicos
consiste simplemente en registrar su peso. Un embarque particular de una fábrica consistió en las baterías
producidas en dos meses diferentes, con el mismo número de baterías producidas en cada mes. El
investigador decide estratificar con base en meses para el muestreo de inspección a fin de observar la
variación mensual. Las muestras aleatorias simples de los pesos de las baterías para los dos meses dieron
las siguientes mediciones (en kilos):
Mes A Mes B
82,5
86,5
83,5
82,8
85,5
83,5
86,0
83,5
83,8
82,5
84,5
85,0
Con un nivel de confianza del 90%, estime con un intervalo de confianza el peso medio de las baterías del
embarque utilizando:
2.a. Muestreo aleatorio estratificado.
2.b. Muestreo aleatorio simple.
3.
Se desea estimar el consumo mensual de una ciudad formada por 8000 familias. Se sabe que los
ingresos en dicha ciudad, vía declaración de la renta, ascienden a 18000000 € mensuales. Se realiza una
encuesta entre 6 hogares elegidos al azar y los resultados de renta y consumo se recogen en esta tabla.
Renta Consumo
3702,44
2840
3339,56
2500
1981,06
1800
3537,04
2600
2519,85
2200
3080,19
2500
Con un intervalo de confianza del 99%, estime el consumo mensual medio por hogar mediante:
3.a. Estimador de razón.
3.b. Muestreo aleatorio simple.
4.
El gerente de un periódico desea estimar el número de ejemplares comprados cada semana por las
familias de una localidad. Los 6500 hogares están agrupados en 600 edificios. Se tiene una encuesta
piloto en la cual se seleccionó una muestra de 4 edificios y se entrevistaron a todas las familias de estos
edificios, obteniéndose los siguientes resultados:
Edificio
Periódicos comprados cada semana por familia
1
2
3
2
3
0
2
1
4
1
3
2
4
0
2
1
2
3
1
3
2
3
2
1
3
1
1
0
2
1
3
4
1
4
1
1
4
2
1
0
3
2
Con un nivel de confianza del 90%, estime por los dos métodos el número de periódicos vendidos en
dicha localidad y el límite para el error de estimación.
6.
La policía de Madrid está interesada en conocer el número de manifestantes que se reunieron en la
Puerta del Sol. Con este dato se puede conocer la cuantía de medios materiales y humanos (policía,
protección civil, personal sanitario, etc.) necesaria para atender futuras concentraciones. Para estimar el
número de manifestantes se toma una fotografía aérea de la zona ocupada por éstos, tras lo cual se traza
sobre ella una cuadrícula que divide el área total en 350 cuadros de 10 metros de lado cada uno.
Posteriormente se numeran y se extrae una muestra aleatoria de 10 de estos cuadros; por último se cuenta
el número de manifestantes que hay en cada uno de los cuadros seleccionados, obteniéndose los
resultados de la tabla:
Nº del cuadro
5.a
5.b
Número de manifestantes en el cuadro
1
260
2
300
3
263
4
306
5
309
6
389
7
305
8
300
9
309
10
298
Estime la densidad de manifestantes por metro cuadrado con un intervalo de confianza del 90%.
Estime el número total de manifestantes concentrados en la Puerta del Sol con un intervalo de
confianza del 99%.